6 Lineare Gleichungssysteme
![]()
Das Lösen linearer Gleichungssysteme
Lösen Sie das lineare Gleichungssystem \(\mathbf{Ax=b}\) nach \(\mathbf{x}\) auf. Die Matrix \(\mathbf{A}\) und der Vektor \(\mathbf{b}\) sind gegeben als \[\mathbf{A} = \left( \begin{array}{rrr} 8 & -8 & 104 \\ 7 & -6 & 82 \\ 5 & 3 & -6 \end{array} \right) \quad \mbox{und} \quad \mathbf{b} = \left( \begin{array}{r} 152 \\ 138 \\ 136 \end{array} \right).\]
Welchen Wert nimmt das Element \(x_1\) an?
Welchen Wert nimmt das Element \(x_2\) an?
Welchen Wert nimmt das Element \(x_3\) an?
Mit Hilfe des Eliminationsverfahrens ergibt sich folgende Lösung:
I. \(\cdot \frac{1}{8}\). \[\begin{aligned} \left(\begin{array}{rrr|r} 1 & -1 & 13 & 19 \\ 7 & -6 & 82 & 138 \\ 5 & 3 & -6 & 136 \end{array}\right) \end{aligned}\]
III. \(- 5\)I. \[\begin{aligned} \left(\begin{array}{rrr|r} 1 & -1 & 13 & 19 \\ 7 & -6 & 82 & 138 \\ 0 & 8 & -71 & 41 \end{array}\right) \end{aligned}\]
II. \(- 7\)I. \[\begin{aligned} \left(\begin{array}{rrr|r} 1 & -1 & 13 & 19 \\ 0 & 1 & -9 & 5 \\ 0 & 8 & -71 & 41 \end{array}\right) \end{aligned}\]
I. \(+ 1\)II. \[\begin{aligned} \left(\begin{array}{rrr|r} 1 & 0 & 4 & 24 \\ 0 & 1 & -9 & 5 \\ 0 & 8 & -71 & 41 \end{array}\right) \end{aligned}\]
III. \(- 8\)II. \[\begin{aligned} \left(\begin{array}{rrr|r} 1 & 0 & 4 & 24 \\ 0 & 1 & -9 & 5 \\ 0 & 0 & 1 & 1 \end{array}\right) \end{aligned}\]
I. \(- 4\)III. \[\begin{aligned} \left(\begin{array}{rrr|r} 1 & 0 & 0 & 20 \\ 0 & 1 & -9 & 5 \\ 0 & 0 & 1 & 1 \end{array}\right) \end{aligned}\]
II. \(+ 9\)III. \[\begin{aligned} \left(\begin{array}{rrr|r} 1 & 0 & 0 & 20 \\ 0 & 1 & 0 & 14 \\ 0 & 0 & 1 & 1 \end{array}\right) \end{aligned}\]
- Das Element \(x_1\) beträgt 20.
- Das Element \(x_2\) beträgt 14.
- Das Element \(x_3\) beträgt 1.
Lösen Sie das lineare Gleichungssystem \(\mathbf{Ax=b}\) nach \(\mathbf{x}\) auf. Die Matrix \(\mathbf{A}\) und der Vektor \(\mathbf{b}\) sind gegeben als \[\mathbf{A} = \left( \begin{array}{rrr} 10 & 50 & -20 \\ 9 & 46 & -19 \\ -3 & -24 & 16 \end{array} \right) \quad \mbox{und} \quad \mathbf{b} = \left( \begin{array}{r} 30 \\ 20 \\ 63 \end{array} \right).\]
Welchen Wert nimmt das Element \(x_1\) an?
Welchen Wert nimmt das Element \(x_2\) an?
Welchen Wert nimmt das Element \(x_3\) an?
Mit Hilfe des Eliminationsverfahrens ergibt sich folgende Lösung:
I. \(\cdot \frac{1}{10}\). \[\begin{aligned} \left(\begin{array}{rrr|r} 1 & 5 & -2 & 3 \\ 9 & 46 & -19 & 20 \\ -3 & -24 & 16 & 63 \end{array}\right) \end{aligned}\]
III. \(+ 3\)I. \[\begin{aligned} \left(\begin{array}{rrr|r} 1 & 5 & -2 & 3 \\ 9 & 46 & -19 & 20 \\ 0 & -9 & 10 & 72 \end{array}\right) \end{aligned}\]
II. \(- 9\)I. \[\begin{aligned} \left(\begin{array}{rrr|r} 1 & 5 & -2 & 3 \\ 0 & 1 & -1 & -7 \\ 0 & -9 & 10 & 72 \end{array}\right) \end{aligned}\]
I. \(- 5\)II. \[\begin{aligned} \left(\begin{array}{rrr|r} 1 & 0 & 3 & 38 \\ 0 & 1 & -1 & -7 \\ 0 & -9 & 10 & 72 \end{array}\right) \end{aligned}\]
III. \(+ 9\)II. \[\begin{aligned} \left(\begin{array}{rrr|r} 1 & 0 & 3 & 38 \\ 0 & 1 & -1 & -7 \\ 0 & 0 & 1 & 9 \end{array}\right) \end{aligned}\]
I. \(- 3\)III. \[\begin{aligned} \left(\begin{array}{rrr|r} 1 & 0 & 0 & 11 \\ 0 & 1 & -1 & -7 \\ 0 & 0 & 1 & 9 \end{array}\right) \end{aligned}\]
II. \(+ 1\)III. \[\begin{aligned} \left(\begin{array}{rrr|r} 1 & 0 & 0 & 11 \\ 0 & 1 & 0 & 2 \\ 0 & 0 & 1 & 9 \end{array}\right) \end{aligned}\]
- Das Element \(x_1\) beträgt 11.
- Das Element \(x_2\) beträgt 2.
- Das Element \(x_3\) beträgt 9.
Lösen Sie das lineare Gleichungssystem \(\mathbf{Ax=b}\) nach \(\mathbf{x}\) auf. Die Matrix \(\mathbf{A}\) und der Vektor \(\mathbf{b}\) sind gegeben als \[\mathbf{A} = \left( \begin{array}{rrr} 5 & -15 & -10 \\ -7 & 22 & 13 \\ 4 & -9 & -10 \end{array} \right) \quad \mbox{und} \quad \mathbf{b} = \left( \begin{array}{r} -25 \\ 30 \\ -29 \end{array} \right).\]
Welchen Wert nimmt das Element \(x_1\) an?
Welchen Wert nimmt das Element \(x_2\) an?
Welchen Wert nimmt das Element \(x_3\) an?
Mit Hilfe des Eliminationsverfahrens ergibt sich folgende Lösung:
I. \(\cdot \frac{1}{5}\). \[\begin{aligned} \left(\begin{array}{rrr|r} 1 & -3 & -2 & -5 \\ -7 & 22 & 13 & 30 \\ 4 & -9 & -10 & -29 \end{array}\right) \end{aligned}\]
III. \(- 4\)I. \[\begin{aligned} \left(\begin{array}{rrr|r} 1 & -3 & -2 & -5 \\ -7 & 22 & 13 & 30 \\ 0 & 3 & -2 & -9 \end{array}\right) \end{aligned}\]
II. \(+ 7\)I. \[\begin{aligned} \left(\begin{array}{rrr|r} 1 & -3 & -2 & -5 \\ 0 & 1 & -1 & -5 \\ 0 & 3 & -2 & -9 \end{array}\right) \end{aligned}\]
I. \(+ 3\)II. \[\begin{aligned} \left(\begin{array}{rrr|r} 1 & 0 & -5 & -20 \\ 0 & 1 & -1 & -5 \\ 0 & 3 & -2 & -9 \end{array}\right) \end{aligned}\]
III. \(- 3\)II. \[\begin{aligned} \left(\begin{array}{rrr|r} 1 & 0 & -5 & -20 \\ 0 & 1 & -1 & -5 \\ 0 & 0 & 1 & 6 \end{array}\right) \end{aligned}\]
I. \(+ 5\)III. \[\begin{aligned} \left(\begin{array}{rrr|r} 1 & 0 & 0 & 10 \\ 0 & 1 & -1 & -5 \\ 0 & 0 & 1 & 6 \end{array}\right) \end{aligned}\]
II. \(+ 1\)III. \[\begin{aligned} \left(\begin{array}{rrr|r} 1 & 0 & 0 & 10 \\ 0 & 1 & 0 & 1 \\ 0 & 0 & 1 & 6 \end{array}\right) \end{aligned}\]
- Das Element \(x_1\) beträgt 10.
- Das Element \(x_2\) beträgt 1.
- Das Element \(x_3\) beträgt 6.
Drei Unbekannte \(u, v\) und \(w\) erfüllen die folgende Gleichungsmatrix: \[\begin{aligned} \left( \begin{array}{ccc|r} 7 & -42 & -7 & -84 \\ 8 & -47 & -9 & -110 \\ -2 & 6 & 9 & 123 \end{array} \right) \end{aligned}\] Bestimmen Sie \(u+v+w\).
Mit Hilfe des Eliminationsverfahrens ergibt sich folgende Lösung:
I. \(\cdot \frac{1}{7}\). \[\begin{aligned} \left(\begin{array}{rrr|r} 1 & -6 & -1 & -12 \\ 8 & -47 & -9 & -110 \\ -2 & 6 & 9 & 123 \end{array}\right) \end{aligned}\]
III. \(+ 2\)I. \[\begin{aligned} \left(\begin{array}{rrr|r} 1 & -6 & -1 & -12 \\ 8 & -47 & -9 & -110 \\ 0 & -6 & 7 & 99 \end{array}\right) \end{aligned}\]
II. \(- 8\)I. \[\begin{aligned} \left(\begin{array}{rrr|r} 1 & -6 & -1 & -12 \\ 0 & 1 & -1 & -14 \\ 0 & -6 & 7 & 99 \end{array}\right) \end{aligned}\]
I. \(+ 6\)II. \[\begin{aligned} \left(\begin{array}{rrr|r} 1 & 0 & -7 & -96 \\ 0 & 1 & -1 & -14 \\ 0 & -6 & 7 & 99 \end{array}\right) \end{aligned}\]
III. \(+ 6\)II. \[\begin{aligned} \left(\begin{array}{rrr|r} 1 & 0 & -7 & -96 \\ 0 & 1 & -1 & -14 \\ 0 & 0 & 1 & 15 \end{array}\right) \end{aligned}\]
I. \(+ 7\)III. \[\begin{aligned} \left(\begin{array}{rrr|r} 1 & 0 & 0 & 9 \\ 0 & 1 & -1 & -14 \\ 0 & 0 & 1 & 15 \end{array}\right) \end{aligned}\]
II. \(+ 1\)III. \[\begin{aligned} \left(\begin{array}{rrr|r} 1 & 0 & 0 & 9 \\ 0 & 1 & 0 & 1 \\ 0 & 0 & 1 & 15 \end{array}\right) \end{aligned}\]
Demnach ist \(u+v+w = 9 + 1 + 15 = 25\).
Drei Unbekannte \(u, v\) und \(w\) erfüllen die folgende Gleichungsmatrix: \[\begin{aligned} \left( \begin{array}{ccc|r} 7 & 35 & -105 & 63 \\ 2 & 11 & -32 & 19 \\ 5 & 31 & -86 & 52 \end{array} \right) \end{aligned}\] Bestimmen Sie \(u+v+w\).
Mit Hilfe des Eliminationsverfahrens ergibt sich folgende Lösung:
I. \(\cdot \frac{1}{7}\). \[\begin{aligned} \left(\begin{array}{rrr|r} 1 & 5 & -15 & 9 \\ 2 & 11 & -32 & 19 \\ 5 & 31 & -86 & 52 \end{array}\right) \end{aligned}\]
III. \(- 5\)I. \[\begin{aligned} \left(\begin{array}{rrr|r} 1 & 5 & -15 & 9 \\ 2 & 11 & -32 & 19 \\ 0 & 6 & -11 & 7 \end{array}\right) \end{aligned}\]
II. \(- 2\)I. \[\begin{aligned} \left(\begin{array}{rrr|r} 1 & 5 & -15 & 9 \\ 0 & 1 & -2 & 1 \\ 0 & 6 & -11 & 7 \end{array}\right) \end{aligned}\]
I. \(- 5\)II. \[\begin{aligned} \left(\begin{array}{rrr|r} 1 & 0 & -5 & 4 \\ 0 & 1 & -2 & 1 \\ 0 & 6 & -11 & 7 \end{array}\right) \end{aligned}\]
III. \(- 6\)II. \[\begin{aligned} \left(\begin{array}{rrr|r} 1 & 0 & -5 & 4 \\ 0 & 1 & -2 & 1 \\ 0 & 0 & 1 & 1 \end{array}\right) \end{aligned}\]
I. \(+ 5\)III. \[\begin{aligned} \left(\begin{array}{rrr|r} 1 & 0 & 0 & 9 \\ 0 & 1 & -2 & 1 \\ 0 & 0 & 1 & 1 \end{array}\right) \end{aligned}\]
II. \(+ 2\)III. \[\begin{aligned} \left(\begin{array}{rrr|r} 1 & 0 & 0 & 9 \\ 0 & 1 & 0 & 3 \\ 0 & 0 & 1 & 1 \end{array}\right) \end{aligned}\]
Demnach ist \(u+v+w = 9 + 3 + 1 = 13\).
Drei Unbekannte \(u, v\) und \(w\) erfüllen die folgende Gleichungsmatrix: \[\begin{aligned} \left( \begin{array}{ccc|r} 4 & -28 & 24 & -36 \\ -2 & 15 & -13 & 19 \\ 8 & -60 & 53 & -62 \end{array} \right) \end{aligned}\] Bestimmen Sie \(u+v+w\).
Mit Hilfe des Eliminationsverfahrens ergibt sich folgende Lösung:
I. \(\cdot \frac{1}{4}\). \[\begin{aligned} \left(\begin{array}{rrr|r} 1 & -7 & 6 & -9 \\ -2 & 15 & -13 & 19 \\ 8 & -60 & 53 & -62 \end{array}\right) \end{aligned}\]
III. \(- 8\)I. \[\begin{aligned} \left(\begin{array}{rrr|r} 1 & -7 & 6 & -9 \\ -2 & 15 & -13 & 19 \\ 0 & -4 & 5 & 10 \end{array}\right) \end{aligned}\]
II. \(+ 2\)I. \[\begin{aligned} \left(\begin{array}{rrr|r} 1 & -7 & 6 & -9 \\ 0 & 1 & -1 & 1 \\ 0 & -4 & 5 & 10 \end{array}\right) \end{aligned}\]
I. \(+ 7\)II. \[\begin{aligned} \left(\begin{array}{rrr|r} 1 & 0 & -1 & -2 \\ 0 & 1 & -1 & 1 \\ 0 & -4 & 5 & 10 \end{array}\right) \end{aligned}\]
III. \(+ 4\)II. \[\begin{aligned} \left(\begin{array}{rrr|r} 1 & 0 & -1 & -2 \\ 0 & 1 & -1 & 1 \\ 0 & 0 & 1 & 14 \end{array}\right) \end{aligned}\]
I. \(+ 1\)III. \[\begin{aligned} \left(\begin{array}{rrr|r} 1 & 0 & 0 & 12 \\ 0 & 1 & -1 & 1 \\ 0 & 0 & 1 & 14 \end{array}\right) \end{aligned}\]
II. \(+ 1\)III. \[\begin{aligned} \left(\begin{array}{rrr|r} 1 & 0 & 0 & 12 \\ 0 & 1 & 0 & 15 \\ 0 & 0 & 1 & 14 \end{array}\right) \end{aligned}\]
Demnach ist \(u+v+w = 12 + 15 + 14 = 41\).
Anwendungen linearer Gleichungssysteme
Aus den beiden Anfangsprodukten \(A_1\) und \(A_2\) werden die drei Endprodukte \(E_1\), \(E_2\) und \(E_3\) gefertigt. Der Bedarf an \(A_1\) und \(A_2\) pro Mengeneinheit der Endprodukte sowie die verfügbaren Lagerbestände an \(A_1\) und \(A_2\) sind der folgenden Tabelle zu entnehmen:
| \(E_1\) | \(E_2\) | \(E_3\) | Lager | |
|---|---|---|---|---|
| \(A_1\) | \(16\) | \(24\) | \(27\) | \(11800\) |
| \(A_2\) | \(17\) | \(25\) | \(2\) | \(7150\) |
Aus technischen Gründen müssen die hergestellten Mengen im Verhältnis \(10 : 4 : 8\) stehen. Berechnen Sie die Produktionsmengen \(E_1\), \(E_2\) und \(E_3\), wenn die Lagerbestände zur Gänze verbraucht werden.
Wie viel kann von \(E_1\) hergestellt werden?
Die Grundgleichung der Bedarfsplanung lautet \(\mathbf{A} \mathbf{x} = \mathbf{b}\). Die Bedarfsmatrix \(\mathbf{A}\) ist gegeben mit \[\begin{aligned} \mathbf{A} = \left( \begin{array}{rrr} 16 & 24 & 27 \\ 17 & 25 & 2 \end{array} \right) \end{aligned}\] Das Herstellungsverhältnis von \(E_1\), \(E_2\) und \(E_3\) beträgt \(10 : 4 : 8\). Der Outputvektor beträgt daher \[\begin{aligned} \mathbf{x} = \left( \begin{array}{ccc} x_1 \\ x_2 \\ x_3 \end{array} \right) = \left( \begin{array}{ccc} 10 x \\ 4 x \\ 8 x \end{array} \right) \end{aligned}\] Da die gesamten Lagerbestände bei der Herstellung verbraucht werden, entspricht der Inputvektor \(\mathbf{b}\) den Lagerbeständen von \(A_1\) und \(A_2\) \[\begin{aligned} \mathbf{b} = \left( \begin{array}{r} 11800 \\ 7150 \end{array} \right) \end{aligned}\] Das zu lösende Gleichungssystem \(\mathbf{A} \mathbf{x} = \mathbf{b}\) lautet daher \[\begin{aligned} \begin{array}{rcrcrcrcccc} 16 \cdot 10 x & + & 24 \cdot 4 x & + & 27 \cdot 8 x & = & 11800 & \Longrightarrow & x & = & 25 \\ 17 \cdot 10 x & + & 25 \cdot 4 x & + & 2 \cdot 8 x & = & 7150 & \Longrightarrow & x & = & 25 \end{array} \end{aligned}\] Das Gleichungssystem besitzt die eindeutige Lösung \(x = 25\). Damit beträgt die Menge von \(E_1\), die hergestellt werden kann: \(E_{1} = 10 \cdot x = 10 \cdot 25 = 250\).
Aus den beiden Anfangsprodukten \(A_1\) und \(A_2\) werden die drei Endprodukte \(E_1\), \(E_2\) und \(E_3\) gefertigt. Der Bedarf an \(A_1\) und \(A_2\) pro Mengeneinheit der Endprodukte sowie die verfügbaren Lagerbestände an \(A_1\) und \(A_2\) sind der folgenden Tabelle zu entnehmen:
| \(E_1\) | \(E_2\) | \(E_3\) | Lager | |
|---|---|---|---|---|
| \(A_1\) | \(16\) | \(14\) | \(24\) | \(7056\) |
| \(A_2\) | \(4\) | \(28\) | \(3\) | \(2800\) |
Aus technischen Gründen müssen die hergestellten Mengen im Verhältnis \(4 : 1 : 2\) stehen. Berechnen Sie die Produktionsmengen \(E_1\), \(E_2\) und \(E_3\), wenn die Lagerbestände zur Gänze verbraucht werden.
Wie viel kann von \(E_1\) hergestellt werden?
Die Grundgleichung der Bedarfsplanung lautet \(\mathbf{A} \mathbf{x} = \mathbf{b}\). Die Bedarfsmatrix \(\mathbf{A}\) ist gegeben mit \[\begin{aligned} \mathbf{A} = \left( \begin{array}{rrr} 16 & 14 & 24 \\ 4 & 28 & 3 \end{array} \right) \end{aligned}\] Das Herstellungsverhältnis von \(E_1\), \(E_2\) und \(E_3\) beträgt \(4 : 1 : 2\). Der Outputvektor beträgt daher \[\begin{aligned} \mathbf{x} = \left( \begin{array}{ccc} x_1 \\ x_2 \\ x_3 \end{array} \right) = \left( \begin{array}{ccc} 4 x \\ 1 x \\ 2 x \end{array} \right) \end{aligned}\] Da die gesamten Lagerbestände bei der Herstellung verbraucht werden, entspricht der Inputvektor \(\mathbf{b}\) den Lagerbeständen von \(A_1\) und \(A_2\) \[\begin{aligned} \mathbf{b} = \left( \begin{array}{r} 7056 \\ 2800 \end{array} \right) \end{aligned}\] Das zu lösende Gleichungssystem \(\mathbf{A} \mathbf{x} = \mathbf{b}\) lautet daher \[\begin{aligned} \begin{array}{rcrcrcrcccc} 16 \cdot 4 x & + & 14 \cdot 1 x & + & 24 \cdot 2 x & = & 7056 & \Longrightarrow & x & = & 56 \\ 4 \cdot 4 x & + & 28 \cdot 1 x & + & 3 \cdot 2 x & = & 2800 & \Longrightarrow & x & = & 56 \end{array} \end{aligned}\] Das Gleichungssystem besitzt die eindeutige Lösung \(x = 56\). Damit beträgt die Menge von \(E_1\), die hergestellt werden kann: \(E_{1} = 4 \cdot x = 4 \cdot 56 = 224\).
Aus den beiden Anfangsprodukten \(A_1\) und \(A_2\) werden die drei Endprodukte \(E_1\), \(E_2\) und \(E_3\) gefertigt. Der Bedarf an \(A_1\) und \(A_2\) pro Mengeneinheit der Endprodukte sowie die verfügbaren Lagerbestände an \(A_1\) und \(A_2\) sind der folgenden Tabelle zu entnehmen:
| \(E_1\) | \(E_2\) | \(E_3\) | Lager | |
|---|---|---|---|---|
| \(A_1\) | \(23\) | \(18\) | \(25\) | \(20175\) |
| \(A_2\) | \(19\) | \(9\) | \(24\) | \(16350\) |
Aus technischen Gründen müssen die hergestellten Mengen im Verhältnis \(5 : 3 : 4\) stehen. Berechnen Sie die Produktionsmengen \(E_1\), \(E_2\) und \(E_3\), wenn die Lagerbestände zur Gänze verbraucht werden.
Wie viel kann von \(E_3\) hergestellt werden?
Die Grundgleichung der Bedarfsplanung lautet \(\mathbf{A} \mathbf{x} = \mathbf{b}\). Die Bedarfsmatrix \(\mathbf{A}\) ist gegeben mit \[\begin{aligned} \mathbf{A} = \left( \begin{array}{rrr} 23 & 18 & 25 \\ 19 & 9 & 24 \end{array} \right) \end{aligned}\] Das Herstellungsverhältnis von \(E_1\), \(E_2\) und \(E_3\) beträgt \(5 : 3 : 4\). Der Outputvektor beträgt daher \[\begin{aligned} \mathbf{x} = \left( \begin{array}{ccc} x_1 \\ x_2 \\ x_3 \end{array} \right) = \left( \begin{array}{ccc} 5 x \\ 3 x \\ 4 x \end{array} \right) \end{aligned}\] Da die gesamten Lagerbestände bei der Herstellung verbraucht werden, entspricht der Inputvektor \(\mathbf{b}\) den Lagerbeständen von \(A_1\) und \(A_2\) \[\begin{aligned} \mathbf{b} = \left( \begin{array}{r} 20175 \\ 16350 \end{array} \right) \end{aligned}\] Das zu lösende Gleichungssystem \(\mathbf{A} \mathbf{x} = \mathbf{b}\) lautet daher \[\begin{aligned} \begin{array}{rcrcrcrcccc} 23 \cdot 5 x & + & 18 \cdot 3 x & + & 25 \cdot 4 x & = & 20175 & \Longrightarrow & x & = & 75 \\ 19 \cdot 5 x & + & 9 \cdot 3 x & + & 24 \cdot 4 x & = & 16350 & \Longrightarrow & x & = & 75 \end{array} \end{aligned}\] Das Gleichungssystem besitzt die eindeutige Lösung \(x = 75\). Damit beträgt die Menge von \(E_3\), die hergestellt werden kann: \(E_{3} = 4 \cdot x = 4 \cdot 75 = 300\).
In der Aula einer Universität steht ein Kaffeeautomat, welcher für die Versorgung der Studenten mit Kaffeemischgetränkten verantwortlich ist. Dieser kann drei Kaffeesorten ausgeben: Espresso, Cappuccino und Latte Macchiato. Für die Zubereitung der Kaffeemischgetränkte werden unterschiedliche Einheiten an Wasser, Milch und Kaffee gebraucht.
Pro ausgegebener Mengeneinheit Espresso werden \(2\) Einheiten Wasser, \(0\) Einheiten Milch und \(5\) Einheiten Kaffee benötigt. Ein Cappuccino setzt sich aus \(5\) Einheiten Wasser, \(6\) Einheiten Milch und \(6\) Einheiten Kaffee zusammen. Ein Latte Macchiato verbraucht \(3\) Einheiten Wasser, \(3\) Einheiten Milch und \(3\) Einheiten Kaffee.
Bei der morgendlichen Neubefüllung des Automaten konnte erfasst werden, dass am Vortag \(1338\) Einheiten Wasser, \(1044\) Einheiten Milch und \(1994\) Einheiten Kaffee verbraucht wurden. Wie viele Mengeneinheiten Latte Macchiato wurden am Vortag ausgegeben?
Die Informationen der Angabe können zu folgender Tabelle zusammengefasst werden:
| Espresso | Cappuccino | Latte Macchiato | |
|---|---|---|---|
| Wasser | \(2\) | \(5\) | \(3\) |
| Milch | \(0\) | \(6\) | \(3\) |
| Kaffee | \(5\) | \(6\) | \(3\) |
Die Grundgleichung der Bedarfsplanung lautet \(\mathbf{A} \mathbf{x}=\mathbf{b}\). Die Bedarfsmatrix \(\mathbf{A}\) ist gegeben mit \[\begin{aligned} \mathbf{A} = \left( \begin{array}{rrr} 2 & 5 & 3 \\ 0 & 6 & 3 \\ 5 & 6 & 3 \end{array} \right) \end{aligned}\] Der Outputvektor beträgt: \[\begin{aligned} \mathbf{x} = \left( \begin{array}{r} x_1 \\ x_2 \\ x_3 \end{array} \right) \end{aligned}\] Da der Automat hatte am Vortag \(1338\) Einheiten Wasser, \(1044\) Einheiten Milch und \(1994\) Einheiten Kaffee verbraucht, dem entspricht der Inputvektor \(\mathbf{b}\): \[\begin{aligned} \mathbf{b} = \left( \begin{array}{r} 1338 \\ 1044 \\ 1994 \end{array} \right) \end{aligned}\] Die zu lösende Matrixgleichung \(\mathbf{A} \mathbf{x}=\mathbf{b}\) lautet daher \[\begin{aligned} \left( \begin{array}{rrr} 2 & 5 & 3 \\ 0 & 6 & 3 \\ 5 & 6 & 3 \end{array} \right) \cdot \left( \begin{array}{r} x_1 \\ x_2 \\ x_3 \end{array} \right) = \left( \begin{array}{r} 1338 \\ 1044 \\ 1994 \end{array} \right) \end{aligned}\] Auflösen nach der gefragten Menge \(\mathbf{x}\) ergibt \(\mathbf{x} = \left( \begin{array}{r} 190 \\ 86 \\ 176 \end{array} \right)\). Die gesuchte Einheitenmenge an Latte Macchiato ist damit \(x_3 = 176.00\).
In der Aula einer Universität steht ein Kaffeeautomat, welcher für die Versorgung der Studenten mit Kaffeemischgetränkten verantwortlich ist. Dieser kann drei Kaffeesorten ausgeben: Espresso, Cappuccino und Latte Macchiato. Für die Zubereitung der Kaffeemischgetränkte werden unterschiedliche Einheiten an Wasser, Milch und Kaffee gebraucht.
Pro ausgegebener Mengeneinheit Espresso werden \(5\) Einheiten Wasser, \(0\) Einheiten Milch und \(6\) Einheiten Kaffee benötigt. Ein Cappuccino setzt sich aus \(2\) Einheiten Wasser, \(3\) Einheiten Milch und \(3\) Einheiten Kaffee zusammen. Ein Latte Macchiato verbraucht \(4\) Einheiten Wasser, \(5\) Einheiten Milch und \(2\) Einheiten Kaffee.
Bei der morgendlichen Neubefüllung des Automaten konnte erfasst werden, dass am Vortag \(1787\) Einheiten Wasser, \(1105\) Einheiten Milch und \(1651\) Einheiten Kaffee verbraucht wurden. Wie viele Mengeneinheiten Cappuccino wurden am Vortag ausgegeben?
Die Informationen der Angabe können zu folgender Tabelle zusammengefasst werden:
| Espresso | Cappuccino | Latte Macchiato | |
|---|---|---|---|
| Wasser | \(5\) | \(2\) | \(4\) |
| Milch | \(0\) | \(3\) | \(5\) |
| Kaffee | \(6\) | \(3\) | \(2\) |
Die Grundgleichung der Bedarfsplanung lautet \(\mathbf{A} \mathbf{x}=\mathbf{b}\). Die Bedarfsmatrix \(\mathbf{A}\) ist gegeben mit \[\begin{aligned} \mathbf{A} = \left( \begin{array}{rrr} 5 & 2 & 4 \\ 0 & 3 & 5 \\ 6 & 3 & 2 \end{array} \right) \end{aligned}\] Der Outputvektor beträgt: \[\begin{aligned} \mathbf{x} = \left( \begin{array}{r} x_1 \\ x_2 \\ x_3 \end{array} \right) \end{aligned}\] Da der Automat hatte am Vortag \(1787\) Einheiten Wasser, \(1105\) Einheiten Milch und \(1651\) Einheiten Kaffee verbraucht, dem entspricht der Inputvektor \(\mathbf{b}\): \[\begin{aligned} \mathbf{b} = \left( \begin{array}{r} 1787 \\ 1105 \\ 1651 \end{array} \right) \end{aligned}\] Die zu lösende Matrixgleichung \(\mathbf{A} \mathbf{x}=\mathbf{b}\) lautet daher \[\begin{aligned} \left( \begin{array}{rrr} 5 & 2 & 4 \\ 0 & 3 & 5 \\ 6 & 3 & 2 \end{array} \right) \cdot \left( \begin{array}{r} x_1 \\ x_2 \\ x_3 \end{array} \right) = \left( \begin{array}{r} 1787 \\ 1105 \\ 1651 \end{array} \right) \end{aligned}\] Auflösen nach der gefragten Menge \(\mathbf{x}\) ergibt \(\mathbf{x} = \left( \begin{array}{r} 185 \\ 55 \\ 188 \end{array} \right)\). Die gesuchte Einheitenmenge an Cappuccino ist damit \(x_2 = 55.00\).
In der Aula einer Universität steht ein Kaffeeautomat, welcher für die Versorgung der Studenten mit Kaffeemischgetränkten verantwortlich ist. Dieser kann drei Kaffeesorten ausgeben: Espresso, Cappuccino und Latte Macchiato. Für die Zubereitung der Kaffeemischgetränkte werden unterschiedliche Einheiten an Wasser, Milch und Kaffee gebraucht.
Die Tabelle zeigt die für die Zubereitung benötigten Einheiten:
| Espresso | Cappuccino | Latte Macchiato | |
|---|---|---|---|
| Wasser | \(4\) | \(2\) | \(6\) |
| Milch | \(0\) | \(3\) | \(4\) |
| Kaffee | \(6\) | \(5\) | \(2\) |
Bspw. besteht ein Espresso aus \(4\) Einheiten Wasser, \(0\) Einheiten Milch und \(6\) Einheiten Kaffee.
Bei der morgendlichen Neubefüllung des Automaten konnte erfasst werden, dass am Vortag \(1512\) Einheiten Wasser, \(1119\) Einheiten Milch und \(1477\) Einheiten Kaffee verbraucht wurden. Wie viele Mengeneinheiten Latte Macchiato wurden am Vortag ausgegeben?
Die Grundgleichung der Bedarfsplanung lautet \(\mathbf{A} \mathbf{x}=\mathbf{b}\). Die Bedarfsmatrix \(\mathbf{A}\) ist gegeben mit \[\begin{aligned} \mathbf{A} = \left( \begin{array}{rrr} 4 & 2 & 6 \\ 0 & 3 & 4 \\ 6 & 5 & 2 \end{array} \right) \end{aligned}\] Der Outputvektor beträgt: \[\begin{aligned} \mathbf{x} = \left( \begin{array}{r} x_1 \\ x_2 \\ x_3 \end{array} \right) \end{aligned}\] Da der Automat hatte am Vortag \(1512\) Einheiten Wasser, \(1119\) Einheiten Milch und \(1477\) Einheiten Kaffee verbraucht, dem entspricht der Inputvektor \(\mathbf{b}\): \[\begin{aligned} \mathbf{b} = \left( \begin{array}{r} 1512 \\ 1119 \\ 1477 \end{array} \right) \end{aligned}\] Die zu lösende Matrixgleichung \(\mathbf{A} \mathbf{x}=\mathbf{b}\) lautet daher \[\begin{aligned} \left( \begin{array}{rrr} 4 & 2 & 6 \\ 0 & 3 & 4 \\ 6 & 5 & 2 \end{array} \right) \cdot \left( \begin{array}{r} x_1 \\ x_2 \\ x_3 \end{array} \right) = \left( \begin{array}{r} 1512 \\ 1119 \\ 1477 \end{array} \right) \end{aligned}\] Auflösen nach der gefragten Menge \(\mathbf{x}\) ergibt \(\mathbf{x} = \left( \begin{array}{r} 59 \\ 161 \\ 159 \end{array} \right)\). Die gesuchte Einheitenmenge an Latte Macchiato ist damit \(x_3 = 159.00\).
Die Flugbahn einer Kugel kann annähernd durch eine quadratische Funktion beschrieben werden
\[\begin{aligned} y = b_1 + b_2 \cdot x + b_3 \cdot x^2, \end{aligned}\]
wobei \(x\) die zurückgelegten Meter der Kugel, \(y\) die Höhe der Kugel in Metern, und \(b_1, b_2, b_3\) die Parameter der Kugel bezeichnen.
Es liegen folgende vier empirische Messungen vor:
| \(x_i\) | \(5\) | \(13\) | \(17\) | \(19\) |
|---|---|---|---|---|
| \(y_i\) | \(101\) | \(178\) | \(193\) | \(182\) |
Welche Flughöhe erreicht die Kugel nach \(27\) Metern?
Die gesuchte Funktion hat die Form \(y = b_1 + b_2 x + b_3 x^2\). Die Parameter \(\mathbf{b} = (b_1, b_2, b_3)^\top\) der Funktion können durch Lösen des Gleichungssystems \(\mathbf{X}^\top \mathbf{X} \mathbf{b} = \mathbf{X}^\top \mathbf{y}\) (Normalgleichungen) bestimmt werden.
Aus den gemessenen Werten ergeben sich folgende Datenmatrizen
\[\begin{aligned} \mathbf{X} & = & \left( \begin{array}{rrr} 1 & 5 & 25 \\ 1 & 13 & 169 \\ 1 & 17 & 289 \\ 1 & 19 & 361 \end{array} \right),~ \quad \mathbf{y} = \left( \begin{array}{r} 101 \\ 178 \\ 193 \\ 182 \end{array} \right), \\ \mathbf{X}^\top \mathbf{X} & = & \left( \begin{array}{rrrr} 1 & 1 & 1 & 1 \\ 5 & 13 & 17 & 19 \\ 25 & 169 & 289 & 361 \end{array} \right) \cdot \left( \begin{array}{rrr} 1 & 5 & 25 \\ 1 & 13 & 169 \\ 1 & 17 & 289 \\ 1 & 19 & 361 \end{array} \right) = \left( \begin{array}{rrr} 4 & 54 & 844 \\ 54 & 844 & 14094 \\ 844 & 14094 & 243028 \end{array} \right), \\ \mathbf{X}^\top \mathbf{y} & = & \left( \begin{array}{rrrr} 1 & 1 & 1 & 1 \\ 5 & 13 & 17 & 19 \\ 25 & 169 & 289 & 361 \end{array} \right) \cdot \left( \begin{array}{r} 101 \\ 178 \\ 193 \\ 182 \end{array} \right) = \left( \begin{array}{r} 654 \\ 9558 \\ 154086 \end{array} \right). \end{aligned}\]
Da es sich bei \(\mathbf{X}^\top \mathbf{X}\) nicht um eine \(2 \times 2\) Matrix handelt, ist es sinnvoll das Gleichungssystem mit Hilfe des Eliminationsverfahrens zu lösen. Die zu lösende Matrixgleichung lautet:
\[\begin{aligned} \left( \begin{array}{rrr} 4 & 54 & 844 \\ 54 & 844 & 14094 \\ 844 & 14094 & 243028 \end{array} \right) \cdot \mathbf{b} = \left( \begin{array}{r} 654 \\ 9558 \\ 154086 \end{array} \right) \end{aligned}\]
Auflösen nach dem gesuchten Vektor \(\mathbf{b}\) ergibt
\[\begin{aligned} \mathbf{b} = \left( \begin{array}{r} 8.067 \\ 21.818 \\ -0.659 \end{array} \right) \end{aligned}\]
Damit ergibt sich folgender quadratischer Zusammenhang
\[\begin{aligned} y = 8.067 + 21.818 \cdot x -0.659 \cdot x^2 . \end{aligned}\]
Um die Flughöhe nach \(27\) Metern zu bestimmen, muss der Funktionswert an der Stelle \(x = 27.00\) berechnet werden:
\[\begin{aligned} f(27) & = & 8.067 + 21.818 \cdot 27 -0.659 \cdot 27^2 \\ f(27) & = & 116.535 \end{aligned}\]
Die folgende Grafik zeigt die vier Messpunkte \((x_i, y_i)\) in grau, die Punkte \((0, b_1)\), \((27, 116.54)\) und \((33.46, 0)\) in dunkelblau sowie die wahre und geschätze quadratische Funktion in hell- bzw. dunkelblau.

Die Flughöhe der Kugel nach \(27\) Metern beträgt \(116.54\) Meter.
Die Flugbahn einer Kugel kann annähernd durch eine quadratische Funktion beschrieben werden
\[\begin{aligned} y = b_1 + b_2 \cdot x + b_3 \cdot x^2, \end{aligned}\]
wobei \(x\) die zurückgelegten Meter der Kugel, \(y\) die Höhe der Kugel in Metern, und \(b_1, b_2, b_3\) die Parameter der Kugel bezeichnen.
Es liegen folgende vier empirische Messungen vor:
| \(x_i\) | \(4\) | \(11\) | \(17\) | \(22\) |
|---|---|---|---|---|
| \(y_i\) | \(98\) | \(208\) | \(235\) | \(223\) |
In welcher Entfernung trifft die Kugel auf dem Boden auf?
Die gesuchte Funktion hat die Form \(y = b_1 + b_2 x + b_3 x^2\). Die Parameter \(\mathbf{b} = (b_1, b_2, b_3)^\top\) der Funktion können durch Lösen des Gleichungssystems \(\mathbf{X}^\top \mathbf{X} \mathbf{b} = \mathbf{X}^\top \mathbf{y}\) (Normalgleichungen) bestimmt werden.
Aus den gemessenen Werten ergeben sich folgende Datenmatrizen
\[\begin{aligned} \mathbf{X} & = & \left( \begin{array}{rrr} 1 & 4 & 16 \\ 1 & 11 & 121 \\ 1 & 17 & 289 \\ 1 & 22 & 484 \end{array} \right),~ \quad \mathbf{y} = \left( \begin{array}{r} 98 \\ 208 \\ 235 \\ 223 \end{array} \right), \\ \mathbf{X}^\top \mathbf{X} & = & \left( \begin{array}{rrrr} 1 & 1 & 1 & 1 \\ 4 & 11 & 17 & 22 \\ 16 & 121 & 289 & 484 \end{array} \right) \cdot \left( \begin{array}{rrr} 1 & 4 & 16 \\ 1 & 11 & 121 \\ 1 & 17 & 289 \\ 1 & 22 & 484 \end{array} \right) = \left( \begin{array}{rrr} 4 & 54 & 910 \\ 54 & 910 & 16956 \\ 910 & 16956 & 332674 \end{array} \right), \\ \mathbf{X}^\top \mathbf{y} & = & \left( \begin{array}{rrrr} 1 & 1 & 1 & 1 \\ 4 & 11 & 17 & 22 \\ 16 & 121 & 289 & 484 \end{array} \right) \cdot \left( \begin{array}{r} 98 \\ 208 \\ 235 \\ 223 \end{array} \right) = \left( \begin{array}{r} 764 \\ 11581 \\ 202583 \end{array} \right). \end{aligned}\]
Da es sich bei \(\mathbf{X}^\top \mathbf{X}\) nicht um eine \(2 \times 2\) Matrix handelt, ist es sinnvoll das Gleichungssystem mit Hilfe des Eliminationsverfahrens zu lösen. Die zu lösende Matrixgleichung lautet:
\[\begin{aligned} \left( \begin{array}{rrr} 4 & 54 & 910 \\ 54 & 910 & 16956 \\ 910 & 16956 & 332674 \end{array} \right) \cdot \mathbf{b} = \left( \begin{array}{r} 764 \\ 11581 \\ 202583 \end{array} \right) \end{aligned}\]
Auflösen nach dem gesuchten Vektor \(\mathbf{b}\) ergibt
\[\begin{aligned} \mathbf{b} = \left( \begin{array}{r} 3.600 \\ 26.832 \\ -0.768 \end{array} \right) \end{aligned}\]
Damit ergibt sich folgender quadratischer Zusammenhang
\[\begin{aligned} y = 3.600 + 26.832 \cdot x -0.768 \cdot x^2 . \end{aligned}\]
Um die Flugweite zu ermitteln muss folgende quadratische Gleichung gelöst werden:
\[\begin{aligned} 0 & = & 3.600 + 26.832 \cdot x -0.768 \cdot x^2 \\ x_1 & = & -0.134 \\ x_2 & = & 35.049 \end{aligned}\]
Da man sich in diesem Kontext nur für die positive Nullstelle der Funktion interessiert, beträgt die Flugweite der Kugel rund \(35.05\) Meter.
Die folgende Grafik zeigt die vier Messpunkte \((x_i, y_i)\) in grau, die Punkte \((0, b_1)\), \((32, 75.30)\) und \((35.05, 0)\) in dunkelblau sowie die wahre und geschätze quadratische Funktion in hell- bzw. dunkelblau.
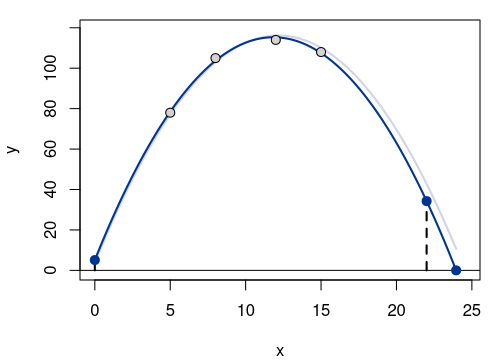
Die Kugel trifft in einer Weite von \(35.05\) Metern auf dem Boden auf.
Die Flugbahn einer Kugel kann annähernd durch eine quadratische Funktion beschrieben werden
\[\begin{aligned} y = b_1 + b_2 \cdot x + b_3 \cdot x^2, \end{aligned}\]
wobei \(x\) die zurückgelegten Meter der Kugel, \(y\) die Höhe der Kugel in Metern, und \(b_1, b_2, b_3\) die Parameter der Kugel bezeichnen.
Es liegen folgende vier empirische Messungen vor:
| \(x_i\) | \(4\) | \(14\) | \(16\) | \(22\) |
|---|---|---|---|---|
| \(y_i\) | \(99\) | \(230\) | \(247\) | \(234\) |
In welcher Entfernung trifft die Kugel auf dem Boden auf?
Die gesuchte Funktion hat die Form \(y = b_1 + b_2 x + b_3 x^2\). Die Parameter \(\mathbf{b} = (b_1, b_2, b_3)^\top\) der Funktion können durch Lösen des Gleichungssystems \(\mathbf{X}^\top \mathbf{X} \mathbf{b} = \mathbf{X}^\top \mathbf{y}\) (Normalgleichungen) bestimmt werden.
Aus den gemessenen Werten ergeben sich folgende Datenmatrizen
\[\begin{aligned} \mathbf{X} & = & \left( \begin{array}{rrr} 1 & 4 & 16 \\ 1 & 14 & 196 \\ 1 & 16 & 256 \\ 1 & 22 & 484 \end{array} \right),~ \quad \mathbf{y} = \left( \begin{array}{r} 99 \\ 230 \\ 247 \\ 234 \end{array} \right), \\ \mathbf{X}^\top \mathbf{X} & = & \left( \begin{array}{rrrr} 1 & 1 & 1 & 1 \\ 4 & 14 & 16 & 22 \\ 16 & 196 & 256 & 484 \end{array} \right) \cdot \left( \begin{array}{rrr} 1 & 4 & 16 \\ 1 & 14 & 196 \\ 1 & 16 & 256 \\ 1 & 22 & 484 \end{array} \right) = \left( \begin{array}{rrr} 4 & 56 & 952 \\ 56 & 952 & 17552 \\ 952 & 17552 & 338464 \end{array} \right), \\ \mathbf{X}^\top \mathbf{y} & = & \left( \begin{array}{rrrr} 1 & 1 & 1 & 1 \\ 4 & 14 & 16 & 22 \\ 16 & 196 & 256 & 484 \end{array} \right) \cdot \left( \begin{array}{r} 99 \\ 230 \\ 247 \\ 234 \end{array} \right) = \left( \begin{array}{r} 810 \\ 12716 \\ 223152 \end{array} \right). \end{aligned}\]
Da es sich bei \(\mathbf{X}^\top \mathbf{X}\) nicht um eine \(2 \times 2\) Matrix handelt, ist es sinnvoll das Gleichungssystem mit Hilfe des Eliminationsverfahrens zu lösen. Die zu lösende Matrixgleichung lautet:
\[\begin{aligned} \left( \begin{array}{rrr} 4 & 56 & 952 \\ 56 & 952 & 17552 \\ 952 & 17552 & 338464 \end{array} \right) \cdot \mathbf{b} = \left( \begin{array}{r} 810 \\ 12716 \\ 223152 \end{array} \right) \end{aligned}\]
Auflösen nach dem gesuchten Vektor \(\mathbf{b}\) ergibt
\[\begin{aligned} \mathbf{b} = \left( \begin{array}{r} 3.113 \\ 26.876 \\ -0.743 \end{array} \right) \end{aligned}\]
Damit ergibt sich folgender quadratischer Zusammenhang
\[\begin{aligned} y = 3.113 + 26.876 \cdot x -0.743 \cdot x^2 . \end{aligned}\]
Um die Flugweite zu ermitteln muss folgende quadratische Gleichung gelöst werden:
\[\begin{aligned} 0 & = & 3.113 + 26.876 \cdot x -0.743 \cdot x^2 \\ x_1 & = & -0.115 \\ x_2 & = & 36.279 \end{aligned}\]
Da man sich in diesem Kontext nur für die positive Nullstelle der Funktion interessiert, beträgt die Flugweite der Kugel rund \(36.28\) Meter.
Die folgende Grafik zeigt die vier Messpunkte \((x_i, y_i)\) in grau, die Punkte \((0, b_1)\), \((32, 102.14)\) und \((36.28, 0)\) in dunkelblau sowie die wahre und geschätze quadratische Funktion in hell- bzw. dunkelblau.
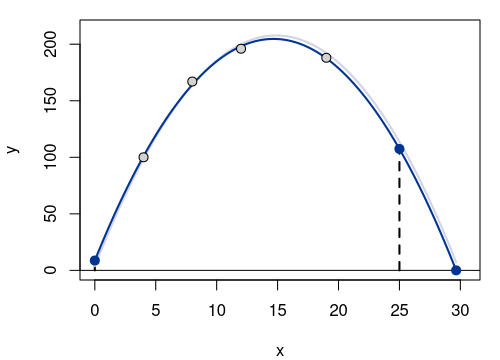
Die Kugel trifft in einer Weite von \(36.28\) Metern auf dem Boden auf.