3 Differentialrechnung
![]()
Differenzieren
Gegeben ist die Funktion \(f(x)= \frac{{(6x^{5}-5x})^3}{2}\). Gesucht ist die erste Ableitung \(f'(x)\) an der Stelle \(x=0.30\).
Da im Nenner nur eine Konstante steht, können wir zur Berechnung der ersten Ableitung die Kettenregel verwenden, indem wir \(z=6x^{5}-5x\) setzen. Die äußere Ableitung von \(\frac{1}{2} z^3\) ist \(3\cdot\frac{1}{2} z^2\). Die innere Ableitung ist \(5\cdot 6x{^4}-5\).
Damit ist die erste Ableitung insgesamt \(f'(x)=\frac{3}{2}\cdot{\left(6x^{5}-5x\right)}^2\cdot \left(5\cdot 6x{^4}-5\right)\).
An der Stelle \(x=0.30\) gilt \(f'(x)=\frac{3}{2}\cdot \left(6\cdot(0.3)^{5}-5\cdot(0.3)\right)^2\cdot \left(5\cdot 6\cdot(0.3){^4}-5\right) =-15.744285\). Also gerundet auf zwei Nachkommastellen: \(f'(0.30) = -15.74\).
Gegeben ist die Funktion \(f(x)= \frac{{(3x^{6}-2x})^5}{8}\). Gesucht ist die erste Ableitung \(f'(x)\) an der Stelle \(x=0.29\).
Da im Nenner nur eine Konstante steht, können wir zur Berechnung der ersten Ableitung die Kettenregel verwenden, indem wir \(z=3x^{6}-2x\) setzen. Die äußere Ableitung von \(\frac{1}{8} z^5\) ist \(5\cdot\frac{1}{8} z^4\). Die innere Ableitung ist \(6\cdot 3x{^5}-2\).
Damit ist die erste Ableitung insgesamt \(f'(x)=\frac{5}{8}\cdot{\left(3x^{6}-2x\right)}^4\cdot \left(6\cdot 3x{^5}-2\right)\).
An der Stelle \(x=0.29\) gilt \(f'(x)=\frac{5}{8}\cdot \left(3\cdot(0.29)^{6}-2\cdot(0.29)\right)^4\cdot \left(6\cdot 3\cdot(0.29){^5}-2\right) =-0.137144\). Also gerundet auf zwei Nachkommastellen: \(f'(0.29) = -0.14\).
Gegeben ist die Funktion \(f(x)= \frac{{(8x^{4}-4x})^7}{8}\). Gesucht ist die erste Ableitung \(f'(x)\) an der Stelle \(x=-0.19\).
Da im Nenner nur eine Konstante steht, können wir zur Berechnung der ersten Ableitung die Kettenregel verwenden, indem wir \(z=8x^{4}-4x\) setzen. Die äußere Ableitung von \(\frac{1}{8} z^7\) ist \(7\cdot\frac{1}{8} z^6\). Die innere Ableitung ist \(4\cdot 8x{^3}-4\).
Damit ist die erste Ableitung insgesamt \(f'(x)=\frac{7}{8}\cdot{\left(8x^{4}-4x\right)}^6\cdot \left(4\cdot 8x{^3}-4\right)\).
An der Stelle \(x=-0.19\) gilt \(f'(x)=\frac{7}{8}\cdot \left(8\cdot(-0.19)^{4}-4\cdot(-0.19)\right)^6\cdot \left(4\cdot 8\cdot(-0.19){^3}-4\right) =-0.772062\). Also gerundet auf zwei Nachkommastellen: \(f'(-0.19) = -0.77\).
Gegeben ist die Funktion \(f(x)= \frac{1}{\sqrt{2x^7+9x}}\). Gesucht ist die erste Ableitung \(f'(x)\) an der Stelle \(x=0.31\).
Zunächst gilt \(\frac{1}{\sqrt{2x^7+9x}}=(2x ^{7} + 9x)^{-\frac{1}{2}}\). Zur Berechnung der ersten Ableitung können wir nun die Kettenregel verwenden, indem wir \(z=2x^7+9x\) setzen. Die äußere Ableitung von \(z^{-\frac{1}{2}}\) ist \(-\frac{1}{2}\cdot z^{-\frac{3}{2}}\). Die innere Ableitung ist \(7 \cdot 2x^6+9 = 14x^6+9\).
Damit ist die erste Ableitung insgesamt \(f'(x)= -\frac{1}{2} \cdot (2x^7+9x)^{-\frac{3}{2}} \cdot \left(14x^6+9\right) = -\frac{14x^6+9}{2 \cdot \sqrt{\left(2x^7+9x\right)^3}}\).
An der Stelle \(x=0.31\) gilt \(f'(x)= -\frac{14\cdot(0.31)^6+9}{2 \cdot \sqrt{\left(2\cdot (0.31)^{7}+9 \cdot (0.31)\right)^3}} =-0.966667\). Also gerundet auf zwei Nachkommastellen: \(f'(0.31) = -0.97\).
Gegeben ist die Funktion \(f(x)= \frac{1}{\sqrt{7x^5+4x}}\). Gesucht ist die erste Ableitung \(f'(x)\) an der Stelle \(x=0.29\).
Zunächst gilt \(\frac{1}{\sqrt{7x^5+4x}}=(7x ^{5} + 4x)^{-\frac{1}{2}}\). Zur Berechnung der ersten Ableitung können wir nun die Kettenregel verwenden, indem wir \(z=7x^5+4x\) setzen. Die äußere Ableitung von \(z^{-\frac{1}{2}}\) ist \(-\frac{1}{2}\cdot z^{-\frac{3}{2}}\). Die innere Ableitung ist \(5 \cdot 7x^4+4 = 35x^4+4\).
Damit ist die erste Ableitung insgesamt \(f'(x)= -\frac{1}{2} \cdot (7x^5+4x)^{-\frac{3}{2}} \cdot \left(35x^4+4\right) = -\frac{35x^4+4}{2 \cdot \sqrt{\left(7x^5+4x\right)^3}}\).
An der Stelle \(x=0.29\) gilt \(f'(x)= -\frac{35\cdot(0.29)^4+4}{2 \cdot \sqrt{\left(7\cdot (0.29)^{5}+4 \cdot (0.29)\right)^3}} =-1.668813\). Also gerundet auf zwei Nachkommastellen: \(f'(0.29) = -1.67\).
Gegeben ist die Funktion \(f(x)= \frac{1}{\sqrt{4x^6+9x}}\). Gesucht ist die erste Ableitung \(f'(x)\) an der Stelle \(x=0.92\).
Zunächst gilt \(\frac{1}{\sqrt{4x^6+9x}}=(4x ^{6} + 9x)^{-\frac{1}{2}}\). Zur Berechnung der ersten Ableitung können wir nun die Kettenregel verwenden, indem wir \(z=4x^6+9x\) setzen. Die äußere Ableitung von \(z^{-\frac{1}{2}}\) ist \(-\frac{1}{2}\cdot z^{-\frac{3}{2}}\). Die innere Ableitung ist \(6 \cdot 4x^5+9 = 24x^5+9\).
Damit ist die erste Ableitung insgesamt \(f'(x)= -\frac{1}{2} \cdot (4x^6+9x)^{-\frac{3}{2}} \cdot \left(24x^5+9\right) = -\frac{24x^5+9}{2 \cdot \sqrt{\left(4x^6+9x\right)^3}}\).
An der Stelle \(x=0.92\) gilt \(f'(x)= -\frac{24\cdot(0.92)^5+9}{2 \cdot \sqrt{\left(4\cdot (0.92)^{6}+9 \cdot (0.92)\right)^3}} =-0.354267\). Also gerundet auf zwei Nachkommastellen: \(f'(0.92) = -0.35\).
Gegeben ist die Funktion \(f(x)= \frac{7x^8}{4x^3}\). Wie lautet die erste Ableitung \(f'(x)\) an der Stelle \(x=0.63\)?
Zur Berechnung der ersten Ableitung könnten wir theoretisch die Quotientenregel benutzen. Bei näherer Betrachtung der Funktion erkennt man jedoch, dass sich diese durch Kürzen wesentlich vereinfachen lässt: \(f(x)= \frac{7x^8}{4x^3} = \frac{7}{4}x^{5}\)
Die erste Ableitung von \(\frac{7}{4}x^{5}\) ist \(5 \cdot \frac{7}{4}x^4\).
An der Stelle \(x=0.63\) gilt damit
\(f'(0.63)= 5 \cdot \frac{7}{4}\cdot (0.63)^4 = 1.378384\). Also gerundet auf zwei Nachkommastellen: \(f'(0.63) = 1.38\).
Gegeben ist die Funktion \(f(x)= \frac{4x^6}{5x^2}\). Wie lautet die erste Ableitung \(f'(x)\) an der Stelle \(x=0.47\)?
Zur Berechnung der ersten Ableitung könnten wir theoretisch die Quotientenregel benutzen. Bei näherer Betrachtung der Funktion erkennt man jedoch, dass sich diese durch Kürzen wesentlich vereinfachen lässt: \(f(x)= \frac{4x^6}{5x^2} = \frac{4}{5}x^{4}\)
Die erste Ableitung von \(\frac{4}{5}x^{4}\) ist \(4 \cdot \frac{4}{5}x^3\).
An der Stelle \(x=0.47\) gilt damit
\(f'(0.47)= 4 \cdot \frac{4}{5}\cdot (0.47)^3 = 0.332234\). Also gerundet auf zwei Nachkommastellen: \(f'(0.47) = 0.33\).
Gegeben ist die Funktion \(f(x)= \frac{4x^5}{5x^3}\). Wie lautet die erste Ableitung \(f'(x)\) an der Stelle \(x=-0.30\)?
Zur Berechnung der ersten Ableitung könnten wir theoretisch die Quotientenregel benutzen. Bei näherer Betrachtung der Funktion erkennt man jedoch, dass sich diese durch Kürzen wesentlich vereinfachen lässt: \(f(x)= \frac{4x^5}{5x^3} = \frac{4}{5}x^{2}\)
Die erste Ableitung von \(\frac{4}{5}x^{2}\) ist \(2 \cdot \frac{4}{5}x\).
An der Stelle \(x=-0.30\) gilt damit
\(f'(-0.30)= 2 \cdot \frac{4}{5}\cdot (-0.30) = -0.48\).
Gegeben ist die Funktion \(f(x)= (5x^{3} + 4x) \cdot e^{\left(6x^{4}+8x\right)}\). Gesucht ist die erste Ableitung \(f'(x)\) an der Stelle \(x=0.17\).
Zur Berechnung der ersten Ableitung können wir die Produktregel benutzen. Die erste Ableitung von \(5x^{3} + 4x\) ist \(3\cdot5x{^2} + 4\). Zur Berechnung der ersten Ableitung von \(e^{\left(6x^{4}+8x\right)}\) können wir die Kettenregel verwenden, indem wir \(z=6x^{4}+8x\) setzen. Die äußere Ableitung von \(e^{z}\) ist \(e^{z}\). Die innere Ableitung ist \(4\cdot6x{^3}+8\). Die erste Ableitung von \(e^{\left(6x^{4}+8x\right)}\) lautet somit \(e^{6x^{4}+8x} \cdot \left( 4\cdot6x{^3}+8\right)\).
Damit ist die erste Ableitung insgesamt \(f'(x)= (3\cdot5x{^2} + 4)\cdot e^{\left(6x^{4}+8x\right)}+ (5x^{3} + 4x)\cdot e^{\left(6x^{4}+8x\right)}\cdot{\left(4\cdot6x{^3}+8\right)}\).
An der Stelle \(x=0.17\) gilt
\(f'(0.17)=
\left(3\cdot5\cdot(0.17){^2} + 4\right) \cdot
e^{\left(6\cdot(0.17)^{4}+8\cdot(0.17)\right)}+
\left(5\cdot(0.17)^{3} + 4\cdot(0.17)\right)
e^{\left(6\cdot(0.17)^{4}+8\cdot(0.17)\right)}\cdot{(4\cdot6\cdot(0.17){^3}+8})
=39.757162\).
Also gerundet auf zwei Nachkommastellen: \(f'(0.17) = 39.76\).
Gegeben ist die Funktion \(f(x)= (4x^{7} + 2x) \cdot e^{\left(9x^{3}+2x\right)}\). Gesucht ist die erste Ableitung \(f'(x)\) an der Stelle \(x=0.40\).
Zur Berechnung der ersten Ableitung können wir die Produktregel benutzen. Die erste Ableitung von \(4x^{7} + 2x\) ist \(7\cdot4x{^6} + 2\). Zur Berechnung der ersten Ableitung von \(e^{\left(9x^{3}+2x\right)}\) können wir die Kettenregel verwenden, indem wir \(z=9x^{3}+2x\) setzen. Die äußere Ableitung von \(e^{z}\) ist \(e^{z}\). Die innere Ableitung ist \(3\cdot9x{^2}+2\). Die erste Ableitung von \(e^{\left(9x^{3}+2x\right)}\) lautet somit \(e^{9x^{3}+2x} \cdot \left( 3\cdot9x{^2}+2\right)\).
Damit ist die erste Ableitung insgesamt \(f'(x)= (7\cdot4x{^6} + 2)\cdot e^{\left(9x^{3}+2x\right)}+ (4x^{7} + 2x)\cdot e^{\left(9x^{3}+2x\right)}\cdot{\left(3\cdot9x{^2}+2\right)}\).
An der Stelle \(x=0.40\) gilt
\(f'(0.40)=
\left(7\cdot4\cdot(0.40){^6} + 2\right) \cdot
e^{\left(9\cdot(0.40)^{3}+2\cdot(0.40)\right)}+
\left(4\cdot(0.40)^{7} + 2\cdot(0.40)\right)
e^{\left(9\cdot(0.40)^{3}+2\cdot(0.40)\right)}\cdot{(3\cdot9\cdot(0.40){^2}+2})
=28.552974\).
Also gerundet auf zwei Nachkommastellen: \(f'(0.40) = 28.55\).
Gegeben ist die Funktion \(f(x)= (2x^{7} + 5x) \cdot e^{\left(9x^{3}+9x\right)}\). Gesucht ist die erste Ableitung \(f'(x)\) an der Stelle \(x=0.35\).
Zur Berechnung der ersten Ableitung können wir die Produktregel benutzen. Die erste Ableitung von \(2x^{7} + 5x\) ist \(7\cdot2x{^6} + 5\). Zur Berechnung der ersten Ableitung von \(e^{\left(9x^{3}+9x\right)}\) können wir die Kettenregel verwenden, indem wir \(z=9x^{3}+9x\) setzen. Die äußere Ableitung von \(e^{z}\) ist \(e^{z}\). Die innere Ableitung ist \(3\cdot9x{^2}+9\). Die erste Ableitung von \(e^{\left(9x^{3}+9x\right)}\) lautet somit \(e^{9x^{3}+9x} \cdot \left( 3\cdot9x{^2}+9\right)\).
Damit ist die erste Ableitung insgesamt \(f'(x)= (7\cdot2x{^6} + 5)\cdot e^{\left(9x^{3}+9x\right)}+ (2x^{7} + 5x)\cdot e^{\left(9x^{3}+9x\right)}\cdot{\left(3\cdot9x{^2}+9\right)}\).
An der Stelle \(x=0.35\) gilt
\(f'(0.35)=
\left(7\cdot2\cdot(0.35){^6} + 5\right) \cdot
e^{\left(9\cdot(0.35)^{3}+9\cdot(0.35)\right)}+
\left(2\cdot(0.35)^{7} + 5\cdot(0.35)\right)
e^{\left(9\cdot(0.35)^{3}+9\cdot(0.35)\right)}\cdot{(3\cdot9\cdot(0.35){^2}+9})
=912.349085\).
Also gerundet auf zwei Nachkommastellen: \(f'(0.35) = 912.35\).
Gegeben ist die Funktion \(f(x)= \ln\left({2x^7}\right)\). Wie lautet die erste Ableitung \(f'(x)\) an der Stelle \(x=2.19\)?
Zur Berechnung der ersten Ableitung können wir die Kettenregel benutzen, indem wir \(z =2x^7\) setzen. Die äußere Ableitung von \(\ln(z)\) ist \(\frac{1}{z}\). Die innere Ableitung ist \(7\cdot2x^{6}\).
Damit ist die erste Ableitung insgesamt \(f'(x)= \frac{1}{2x^7}\cdot7\cdot 2x^{6} = \frac{7}{x}\).
An der Stelle \(x=2.19\) gilt \(f'(2.19)= \frac{7}{2.19}
= 3.196347\).
Also gerundet auf zwei Nachkommastellen: \(f'(2.19) = 3.20\).
Gegeben ist die Funktion \(f(x)= \ln\left({6x^9}\right)\). Wie lautet die erste Ableitung \(f'(x)\) an der Stelle \(x=2.71\)?
Zur Berechnung der ersten Ableitung können wir die Kettenregel benutzen, indem wir \(z =6x^9\) setzen. Die äußere Ableitung von \(\ln(z)\) ist \(\frac{1}{z}\). Die innere Ableitung ist \(9\cdot6x^{8}\).
Damit ist die erste Ableitung insgesamt \(f'(x)= \frac{1}{6x^9}\cdot9\cdot 6x^{8} = \frac{9}{x}\).
An der Stelle \(x=2.71\) gilt \(f'(2.71)= \frac{9}{2.71}
= 3.321033\).
Also gerundet auf zwei Nachkommastellen: \(f'(2.71) = 3.32\).
Gegeben ist die Funktion \(f(x)= \ln\left({9x^8}\right)\). Wie lautet die erste Ableitung \(f'(x)\) an der Stelle \(x=1.94\)?
Zur Berechnung der ersten Ableitung können wir die Kettenregel benutzen, indem wir \(z =9x^8\) setzen. Die äußere Ableitung von \(\ln(z)\) ist \(\frac{1}{z}\). Die innere Ableitung ist \(8\cdot9x^{7}\).
Damit ist die erste Ableitung insgesamt \(f'(x)= \frac{1}{9x^8}\cdot8\cdot 9x^{7} = \frac{8}{x}\).
An der Stelle \(x=1.94\) gilt \(f'(1.94)= \frac{8}{1.94}
= 4.123711\).
Also gerundet auf zwei Nachkommastellen: \(f'(1.94) = 4.12\).
Interpretationen der Ableitung
Zwischen 1998 und 2018 entwickelt sich die Anzahl verschickter Nachrichten in einem sozialen Netzwerk nach der Formel \(f(t) = 8 + 0.7t + 0.04t^2 + 0.002t^3\) Mio./Jahr, (\(1998\): \(t=0\)). Wie groß ist die momentane Zuwachsrate im Jahr 2008?
Das Jahr \(2008\) entspricht \(t=10\). Die momentane Zuwachsrate an der Stelle \(t\) ergibt sich aus der Ableitung \(f'(t)\): \[\begin{aligned} f'(t) & = & 0.7+2 \cdot 0.04 \cdot t + 3 \cdot 0.002 \cdot t^2\\ f'(10) & = & 0.7+0.08 \cdot 10 + 0.006 \cdot 10^2 \,\, = \,\, 2.10 \end{aligned}\] Die Anzahl verschickter Nachrichten wächst momentan (im Jahr \(2008\)) um \(2.10\) Mio./Jahr.
Zwischen 2002 und 2015 entwickelt sich die Anzahl verschickter Nachrichten in einem sozialen Netzwerk nach der Formel \(f(t) = 9 + 0.7t + 0.04t^2 + 0.002t^3\) Mio./Jahr, (\(2002\): \(t=0\)). Wie groß ist die momentane Zuwachsrate im Jahr 2008?
Das Jahr \(2008\) entspricht \(t=6\). Die momentane Zuwachsrate an der Stelle \(t\) ergibt sich aus der Ableitung \(f'(t)\): \[\begin{aligned} f'(t) & = & 0.7+2 \cdot 0.04 \cdot t + 3 \cdot 0.002 \cdot t^2\\ f'(6) & = & 0.7+0.08 \cdot 6 + 0.006 \cdot 6^2 \,\, = \,\, 1.40 \end{aligned}\] Die Anzahl verschickter Nachrichten wächst momentan (im Jahr \(2008\)) um \(1.40\) Mio./Jahr.
Zwischen 1999 und 2014 entwickelt sich die Anzahl verschickter Nachrichten in einem sozialen Netzwerk nach der Formel \(f(t) = 9 + 0.1t + 0.03t^2 + 0.001t^3\) Mio./Jahr, (\(1999\): \(t=0\)). Wie groß ist die momentane Zuwachsrate im Jahr 2011?
Das Jahr \(2011\) entspricht \(t=12\). Die momentane Zuwachsrate an der Stelle \(t\) ergibt sich aus der Ableitung \(f'(t)\): \[\begin{aligned} f'(t) & = & 0.1+2 \cdot 0.03 \cdot t + 3 \cdot 0.001 \cdot t^2\\ f'(12) & = & 0.1+0.06 \cdot 12 + 0.003 \cdot 12^2 \,\, = \,\, 1.25 \end{aligned}\] Die Anzahl verschickter Nachrichten wächst momentan (im Jahr \(2011\)) um \(1.25\) Mio./Jahr.
Berechnen Sie die Elastizität der Funktion \(f(x)= (0.81+2.83x)^{0.14}\) an der Stelle \(x=1.98\).
Zur Berechnung der Elastizität verwenden wir die Formel \(\epsilon(x)= \frac{f'(x)}{f(x)}\cdot x\). Die erste Ableitung von \(f(x) = (0.81+2.83x)^{0.14}\) ist nach der Kettenregel \(f'(x) = 0.14\cdot(0.81+2.83x)^{-0.86}\cdot 2.83 = 0.3962\cdot{(0.81+2.83x)^{-0.86}}\).
An der Stelle \(x=1.98\) gilt \(\epsilon(1.98)= \frac{0.3962\cdot(0.81+2.83\cdot(1.98))^{-0.86}} {(0.81+2.83\cdot(1.98))^{0.14}}\cdot 1.98 =0.122318\).
Also gerundet auf zwei Nachkommastellen: \(\epsilon(1.98) = 0.12\).
Berechnen Sie die Elastizität der Funktion \(f(x)= (0.72+5.34x)^{0.18}\) an der Stelle \(x=3.90\).
Zur Berechnung der Elastizität verwenden wir die Formel \(\epsilon(x)= \frac{f'(x)}{f(x)}\cdot x\). Die erste Ableitung von \(f(x) = (0.72+5.34x)^{0.18}\) ist nach der Kettenregel \(f'(x) = 0.18\cdot(0.72+5.34x)^{-0.82}\cdot 5.34 = 0.9612\cdot{(0.72+5.34x)^{-0.82}}\).
An der Stelle \(x=3.90\) gilt \(\epsilon(3.90)= \frac{0.9612\cdot(0.72+5.34\cdot(3.90))^{-0.82}} {(0.72+5.34\cdot(3.90))^{0.18}}\cdot 3.90 =0.173985\).
Also gerundet auf zwei Nachkommastellen: \(\epsilon(3.90) = 0.17\).
Berechnen Sie die Elastizität der Funktion \(f(x)= (0.67+7.65x)^{0.56}\) an der Stelle \(x=3.74\).
Zur Berechnung der Elastizität verwenden wir die Formel \(\epsilon(x)= \frac{f'(x)}{f(x)}\cdot x\). Die erste Ableitung von \(f(x) = (0.67+7.65x)^{0.56}\) ist nach der Kettenregel \(f'(x) = 0.56\cdot(0.67+7.65x)^{-0.44}\cdot 7.65 = 4.284\cdot{(0.67+7.65x)^{-0.44}}\).
An der Stelle \(x=3.74\) gilt \(\epsilon(3.74)= \frac{4.284\cdot(0.67+7.65\cdot(3.74))^{-0.44}} {(0.67+7.65\cdot(3.74))^{0.56}}\cdot 3.74 =0.547186\).
Also gerundet auf zwei Nachkommastellen: \(\epsilon(3.74) = 0.55\).
Kurvendiskussion
Die folgende Grafik zeigt drei kritische Punkte der Funktion \(f(x)\) bzw. ihrer Ableitung \(f'(x)\). Die Funktion ist gegeben durch: \[\begin{aligned} f(x)= 0.73 x^3 - 2.39 x^2 - 1.26 x + 4.68 \end{aligned}\] Welchen Wert hat die zweite Ableitung \(f''(x)\) im Punkt C?

Beim Punkt C handelt es sich um ein lokales Minimum der Funktion \(f(x)\). Die erste Ableitung in diesem Punkt ist somit \(0\), die zweite Ableitung ist positiv. Die Ableitungen ergeben sich wie folgt: \[\begin{aligned} f'(x) &=& 2.19 x^2 - 4.78 x - 1.26\\ f''(x) &=& 4.38 x - 4.78 \end{aligned}\] Setzen wir die erste Ableitung \(0\) und lösen die quadratische Gleichung, so erhalten wir die möglichen Lösungen \(x_1=-0.23771\) und \(x_2=2.420358\). Für die zweite Ableitung in diesen Punkten gilt \(f''(x_1)=-5.821168<0\) bzw. \(f''(x_2)=5.821168>0\). Das lokale Minimum im Punkt C befindet sich also an der Stelle \(x_2=2.420358\), der Wert der zweiten Ableitung beträgt hier \(f''(x_2) \approx 5.82\).
Die folgende Grafik zeigt drei kritische Punkte der Funktion \(f(x)\) bzw. ihrer Ableitung \(f'(x)\). Die Funktion ist gegeben durch: \[\begin{aligned} f(x)= 1.38 x^3 - 1.74 x^2 - 1.22 x + 5.99 \end{aligned}\] Welchen Wert hat die zweite Ableitung \(f''(x)\) im Punkt A?
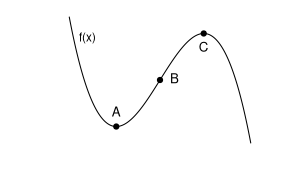
Beim Punkt A handelt es sich um ein lokales Maximum der Funktion \(f(x)\). Die erste Ableitung in diesem Punkt ist somit \(0\), die zweite Ableitung ist negativ. Die Ableitungen ergeben sich wie folgt: \[\begin{aligned} f'(x) &=& 4.14 x^2 - 3.48 x - 1.22\\ f''(x) &=& 8.28 x - 3.48 \end{aligned}\] Setzen wir die erste Ableitung \(0\) und lösen die quadratische Gleichung, so erhalten wir die möglichen Lösungen \(x_1=-0.266245\) und \(x_2=1.106824\). Für die zweite Ableitung in diesen Punkten gilt \(f''(x_1)=-5.684505<0\) bzw. \(f''(x_2)=5.684505>0\). Das lokale Maximum im Punkt A befindet sich also an der Stelle \(x_1=-0.266245\), der Wert der zweiten Ableitung beträgt hier \(f''(x_1) \approx -5.68\).
Die folgende Grafik zeigt drei kritische Punkte der Funktion \(f(x)\) bzw. ihrer Ableitung \(f'(x)\). Die Funktion ist gegeben durch: \[\begin{aligned} f(x)= -0.76 x^3 + 1.27 x^2 + 1.01 x + 5.31 \end{aligned}\] Welchen Wert hat die zweite Ableitung \(f''(x)\) im Punkt C?
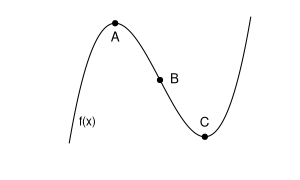
Beim Punkt C handelt es sich um ein lokales Maximum der Funktion \(f(x)\). Die erste Ableitung in diesem Punkt ist somit \(0\), die zweite Ableitung ist negativ. Die Ableitungen ergeben sich wie folgt: \[\begin{aligned} f'(x) &=& -2.28 x^2 + 2.54 x + 1.01\\ f''(x) &=& -4.56 x + 2.54 \end{aligned}\] Setzen wir die erste Ableitung \(0\) und lösen die quadratische Gleichung, so erhalten wir die möglichen Lösungen \(x_1=-0.310883\) und \(x_2=1.424918\). Für die zweite Ableitung in diesen Punkten gilt \(f''(x_1)=3.957626>0\) bzw. \(f''(x_2)=-3.957626<0\). Das lokale Maximum im Punkt C befindet sich also an der Stelle \(x_2=1.424918\), der Wert der zweiten Ableitung beträgt hier \(f''(x_2) \approx -3.96\).
Gegeben ist die Funktion \(f(x)= 2x^2 - 3x + 18\). Führen Sie eine Kurvendiskussion durch und kreuzen Sie alle richtigen Aussagen an.
Die erste und zweite Ableitung der Funktion \(f(x)\) sind gegeben durch \[\begin{aligned}
f'(x) &= &2\cdot2x - 3 = 4x - 3 \\
f''(x) &= &4
\end{aligned}\] Im Punkt \(x=-0.34\) gilt daher \[\begin{aligned}
f'(-0.34) = 4\cdot(-0.34) - 3 = -4.36
\end{aligned}\] Somit ist die Steigung der Tangente an \(f(x)\) in diesem Punkt kleiner \(-1.36\).
Weiters gilt im Punkt \(x=-0.73\) \[\begin{aligned}
f'(-0.73) = 4\cdot(-0.73) - 3 = -5.92 < 0
\end{aligned}\] Somit ist \(f(x)\) in diesem Punkt fallend.
Im Punkt \(x=0.75\) gilt \[\begin{aligned}
f'(0.75) = 4\cdot(0.75) - 3 = 0
\end{aligned}\] Der Punkt \(x=0.75\) ist somit ein stationärer Punkt. Da für die zweite Ableitung gilt \[\begin{aligned}
f''(0.75) = 4 > 0,
\end{aligned}\] handelt es sich dabei um ein lokales Minimum.
Die zweite Ableitung im Punkt \(x=0.12\) ist positiv: \[\begin{aligned}
f''(0.12) = 4 > 0.
\end{aligned}\]
Da für die zweite Ableitung im Punkt \(x=2.10\) gilt \[\begin{aligned}
f''(2.10) = 4 > 0,
\end{aligned}\] ist \(f(x)\) in diesem Punkt konvex.
- Falsch
- Falsch
- Richtig
- Falsch
- Richtig
Gegeben ist die Funktion \(f(x)= 5x^2 - 2x - 16\). Führen Sie eine Kurvendiskussion durch und kreuzen Sie alle richtigen Aussagen an.
Die erste und zweite Ableitung der Funktion \(f(x)\) sind gegeben durch \[\begin{aligned}
f'(x) &= &2\cdot5x - 2 = 10x - 2 \\
f''(x) &= &10
\end{aligned}\] Im Punkt \(x=1.14\) gilt daher \[\begin{aligned}
f'(1.14) = 10\cdot(1.14) - 2 = 9.40
\end{aligned}\] Somit ist die erste Ableitung von \(f(x)\) in diesem Punkt größer \(0\).
Weiters gilt im Punkt \(x=2.03\) \[\begin{aligned}
f'(2.03) = 10\cdot(2.03) - 2 = 18.30 > 0
\end{aligned}\] Somit ist \(f(x)\) in diesem Punkt steigend.
Im Punkt \(x=0.20\) gilt \[\begin{aligned}
f'(0.20) = 10\cdot(0.20) - 2 = 0
\end{aligned}\] Der Punkt \(x=0.20\) ist somit ein stationärer Punkt. Da für die zweite Ableitung gilt \[\begin{aligned}
f''(0.20) = 10 > 0,
\end{aligned}\] handelt es sich dabei um ein lokales Minimum.
Die zweite Ableitung im Punkt \(x=1.16\) ist positiv: \[\begin{aligned}
f''(1.16) = 10 > 0.
\end{aligned}\]
Da für die zweite Ableitung im Punkt \(x=1.82\) gilt \[\begin{aligned}
f''(1.82) = 10 > 0,
\end{aligned}\] ist \(f(x)\) in diesem Punkt konvex.
- Falsch
- Richtig
- Richtig
- Richtig
- Falsch
Gegeben ist die Funktion \(f(x)= -3x^2 + 9x - 20\). Führen Sie eine Kurvendiskussion durch und kreuzen Sie alle richtigen Aussagen an.
Die erste und zweite Ableitung der Funktion \(f(x)\) sind gegeben durch \[\begin{aligned}
f'(x) &= &-2\cdot3x + 9 = -6x + 9 \\
f''(x) &= &-6
\end{aligned}\] Im Punkt \(x=3.07\) gilt daher \[\begin{aligned}
f'(3.07) = -6\cdot(3.07) + 9 = -9.42
\end{aligned}\] Somit ist die Steigung der Tangente an \(f(x)\) in diesem Punkt größer \(-18.42\).
Weiters gilt im Punkt \(x=2.04\) \[\begin{aligned}
f'(2.04) = -6\cdot(2.04) + 9 = -3.24 < 0
\end{aligned}\] Somit ist \(f(x)\) in diesem Punkt fallend.
Im Punkt \(x=1.50\) gilt \[\begin{aligned}
f'(1.50) = -6\cdot(1.50) + 9 = 0
\end{aligned}\] Der Punkt \(x=1.50\) ist somit ein stationärer Punkt. Da für die zweite Ableitung gilt \[\begin{aligned}
f''(1.50) = -6 < 0,
\end{aligned}\] handelt es sich dabei um ein lokales Maximum.
Die zweite Ableitung im Punkt \(x=1.38\) ist negativ: \[\begin{aligned}
f''(1.38) = -6 < 0.
\end{aligned}\]
Da für die zweite Ableitung im Punkt \(x=-0.13\) gilt \[\begin{aligned}
f''(-0.13) = -6 < 0,
\end{aligned}\] ist \(f(x)\) in diesem Punkt konkav.
- Falsch
- Falsch
- Falsch
- Richtig
- Falsch
Gegeben ist die Funktion \(f(x)= 3 x ^{3} \cdot \exp{(-0.5 x + 5)}\).
Führen Sie eine Kurvendiskussion durch und kreuzen Sie alle richtigen Aussagen an.
Die erste und zweite Ableitung der Funktion \(f(x)\) sind gegeben durch \[\begin{aligned} f'(x) & = & \exp(-0.5x + 5) \left( 9 x^{2} -1.5x^3 \right)\\ f''(x) & = & \exp(-0.5x + 5) \left(-4.5x^{2} + 0.75x^3 + 18x -4.5x^{2}\right) \\ &=& \exp(-0.5x + 5) \left(-9x^{2} + 0.75x^3 + 18x^{} \right) \end{aligned}\]
Im Punkt \(x=4.5\) gilt daher \[\begin{aligned}
f'(4.5) = 712.72
\end{aligned}\] Somit ist die Steigung der Tangente an \(f(x)\) in diesem Punkt größer \(-339.65\).
Weiters gilt im Punkt \(x=3.1\) \[\begin{aligned}
f'(3.1) = 1316.83 > 0
\end{aligned}\] Somit ist \(f(x)\) in diesem Punkt steigend.
Im Punkt \(x=0\) gilt \[\begin{aligned}
f'(0) = 0.00
\end{aligned}\] Der Punkt \(x=0\) ist somit ein stationärer Punkt. Da für die zweite Ableitung gilt \[\begin{aligned}
f''(0) = 0 ,
\end{aligned}\] handelt es sich dabei um einen Sattelpunkt.
Die zweite Ableitung im Punkt \(x=8.19\) ist negativ: \[\begin{aligned}
f''(8.19) = -109.38 < 0.
\end{aligned}\]
Da für die zweite Ableitung im Punkt \(x=2.7\) gilt \[\begin{aligned} f''(2.7) = -86.48 < 0, \end{aligned}\] ist \(f(x)\) in diesem Punkt konkav.

- Richtig
- Richtig
- Richtig
- Richtig
- Falsch
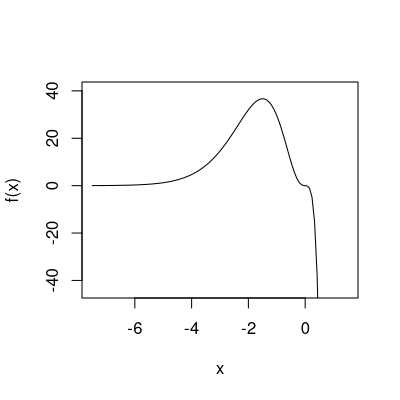
Gegeben ist die Funktion \(f(x)= 3 x ^{3} \cdot \exp{(-2 x + 5)}\).
Führen Sie eine Kurvendiskussion durch und kreuzen Sie alle richtigen Aussagen an.
Die erste und zweite Ableitung der Funktion \(f(x)\) sind gegeben durch \[\begin{aligned} f'(x) & = & \exp(-2x + 5) \left( 9 x^{2} -6x^3 \right)\\ f''(x) & = & \exp(-2x + 5) \left(-18x^{2} + 12x^3 + 18x -18x^{2}\right) \\ &=& \exp(-2x + 5) \left(-36x^{2} + 12x^3 + 18x^{} \right) \end{aligned}\]
Im Punkt \(x=1.37\) gilt daher \[\begin{aligned}
f'(1.37) = 14.03
\end{aligned}\] Somit ist die Steigung der Tangente an \(f(x)\) in diesem Punkt gleich \(14.03\).
Weiters gilt im Punkt \(x=2.13\) \[\begin{aligned}
f'(2.13) = -35.94 < 0
\end{aligned}\] Somit ist \(f(x)\) in diesem Punkt fallend.
Im Punkt \(x=0\) gilt \[\begin{aligned}
f'(0) = 0.00
\end{aligned}\] Der Punkt \(x=0\) ist somit ein stationärer Punkt. Da für die zweite Ableitung gilt \[\begin{aligned}
f''(0) = 0 ,
\end{aligned}\] handelt es sich dabei um einen Sattelpunkt.
Die zweite Ableitung im Punkt \(x=2\) ist negativ: \[\begin{aligned}
f''(2) = -32.62 < 0.
\end{aligned}\]
Da für die zweite Ableitung im Punkt \(x=2.87\) gilt \[\begin{aligned} f''(2.87) = 18.52 > 0, \end{aligned}\] ist \(f(x)\) in diesem Punkt konvex.
- Falsch
- Richtig
- Richtig
- Richtig
- Richtig
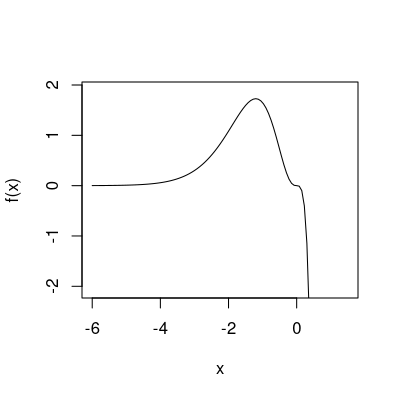
Gegeben ist die Funktion \(f(x)= 3 x ^{3} \cdot \exp{(-4.5 x + 4)}\).
Führen Sie eine Kurvendiskussion durch und kreuzen Sie alle richtigen Aussagen an.
Die erste und zweite Ableitung der Funktion \(f(x)\) sind gegeben durch \[\begin{aligned} f'(x) & = & \exp(-4.5x + 4) \left( 9 x^{2} -13.5x^3 \right)\\ f''(x) & = & \exp(-4.5x + 4) \left(-40.5x^{2} + 60.75x^3 + 18x -40.5x^{2}\right) \\ &=& \exp(-4.5x + 4) \left(-81x^{2} + 60.75x^3 + 18x^{} \right) \end{aligned}\]
Im Punkt \(x=1.19\) gilt daher \[\begin{aligned}
f'(1.19) = -2.58
\end{aligned}\] Somit ist die Steigung der Tangente an \(f(x)\) in diesem Punkt gleich \(-2.58\).
Weiters gilt im Punkt \(x=0.69\) \[\begin{aligned}
f'(0.69) = -0.37 < 0
\end{aligned}\] Somit ist \(f(x)\) in diesem Punkt fallend.
Im Punkt \(x=0\) gilt \[\begin{aligned}
f'(0) = 0.00
\end{aligned}\] Der Punkt \(x=0\) ist somit ein stationärer Punkt. Da für die zweite Ableitung gilt \[\begin{aligned}
f''(0) = 0 ,
\end{aligned}\] handelt es sich dabei um einen Sattelpunkt.
Die zweite Ableitung im Punkt \(x=0.58\) ist negativ: \[\begin{aligned}
f''(0.58) = -19.89 < 0.
\end{aligned}\]
Da für die zweite Ableitung im Punkt \(x=0.03\) gilt \[\begin{aligned} f''(0.03) = 22.36 > 0, \end{aligned}\] ist \(f(x)\) in diesem Punkt konvex.
- Richtig
- Falsch
- Richtig
- Falsch
- Richtig
Optimierung
Ein Monopolanbieter besitzt die nachfolgende inverse Nachfragefunktion \(D^{-1} (x)\) und Kostenfunktion \(C(x)\): \[\begin{aligned} D^{-1} (x): ~ p &=& -20x + 620\\ C(x) &=& 0.09811x^3 - 6.141x^2 + 220x + 1500 \end{aligned}\] Bei welchem Angebot \(x\) erzielt der Monopolist maximalen Gewinn?
Die Erlösfunktion nimmt folgende Form an: \[\begin{aligned} R(x) = p\cdot x = (-20x+620)x = -20x^2 + 620x \end{aligned}\] Die Gewinnfunktion lautet: \[\begin{aligned} \pi &=& R(x) - C(x)\\ &=& -20x^2 + 620x -(0.09811x^3-6.141x^2+220x+1500)\\ &=& -0.09811x^3 -13.859x^2 + 400x - 1500 \end{aligned}\] Nun bilden wir die erste Ableitung der Gewinnfunktion und erhalten folgende quadratische Funktion: \[\begin{aligned} \pi' = -0.29433x^2 -27.718x + 400 = 0 \end{aligned}\] Mit Hilfe der quadratischen Formel berechnen wir nun das Angebot, bei dem der Monopolist den maximalen Gewinn erzielt. \[\begin{aligned} x_1,_2 &=& \frac{-B \pm \sqrt{(B^2-4AC)}}{2A}\\ x_1,_2 &=& \frac{-(-27.718) \pm \sqrt{(-27.718)^2-(4\cdot (-0.29433)\cdot 400)}}{2\cdot (-0.29433)}\\ x_1 &=& 12.714459\\ x_2 &=& -106.887665 \end{aligned}\] Die Funktion besitzt kritische Punkte in \(x_1 = 12.714459\) und \(x_2= -106.887665\). Um sicherzugehen, dass die positive Lösung tatsächlich ein Maximum ist, berechnen wir die zweite Ableitung an der Stelle \(x_1 = 12.714459\): \[\begin{aligned} \pi''(x) = -0.58866x - 27.718 \\ \pi''(12.714459) = -35.202493 < 0. \end{aligned}\] Daher handelt es sich tatsächlich um ein Maximum.
Bei einem Angebot von \(x = 12.71\) Stück erzielt der Monopolist maximalen Gewinn.
Ein Monopolanbieter besitzt die nachfolgende inverse Nachfragefunktion \(D^{-1} (x)\) und Kostenfunktion \(C(x)\): \[\begin{aligned} D^{-1} (x): ~ p &=& -20x + 640\\ C(x) &=& 0.01541x^3 - 4.0657x^2 + 160x + 1400 \end{aligned}\] Bei welchem Angebot \(x\) erzielt der Monopolist maximalen Gewinn?
Die Erlösfunktion nimmt folgende Form an: \[\begin{aligned} R(x) = p\cdot x = (-20x+640)x = -20x^2 + 640x \end{aligned}\] Die Gewinnfunktion lautet: \[\begin{aligned} \pi &=& R(x) - C(x)\\ &=& -20x^2 + 640x -(0.01541x^3-4.0657x^2+160x+1400)\\ &=& -0.01541x^3 -15.9343x^2 + 480x - 1400 \end{aligned}\] Nun bilden wir die erste Ableitung der Gewinnfunktion und erhalten folgende quadratische Funktion: \[\begin{aligned} \pi' = -0.04623x^2 -31.8686x + 480 = 0 \end{aligned}\] Mit Hilfe der quadratischen Formel berechnen wir nun das Angebot, bei dem der Monopolist den maximalen Gewinn erzielt. \[\begin{aligned} x_1,_2 &=& \frac{-B \pm \sqrt{(B^2-4AC)}}{2A}\\ x_1,_2 &=& \frac{-(-31.8686) \pm \sqrt{(-31.8686)^2-(4\cdot (-0.04623)\cdot 480)}}{2\cdot (-0.04623)}\\ x_1 &=& 14.746396\\ x_2 &=& -704.095304 \end{aligned}\] Die Funktion besitzt kritische Punkte in \(x_1 = 14.746396\) und \(x_2= -704.095304\). Um sicherzugehen, dass die positive Lösung tatsächlich ein Maximum ist, berechnen wir die zweite Ableitung an der Stelle \(x_1 = 14.746396\): \[\begin{aligned} \pi''(x) = -0.09246x - 31.8686 \\ \pi''(14.746396) = -33.232052 < 0. \end{aligned}\] Daher handelt es sich tatsächlich um ein Maximum.
Bei einem Angebot von \(x = 14.75\) Stück erzielt der Monopolist maximalen Gewinn.
Ein Monopolanbieter besitzt die nachfolgende inverse Nachfragefunktion \(D^{-1} (x)\) und Kostenfunktion \(C(x)\): \[\begin{aligned} D^{-1} (x): ~ p &=& -20x + 690\\ C(x) &=& 0.08831x^3 - 7.6893x^2 + 255x + 5900 \end{aligned}\] Bei welchem Angebot \(x\) erzielt der Monopolist maximalen Gewinn?
Die Erlösfunktion nimmt folgende Form an: \[\begin{aligned} R(x) = p\cdot x = (-20x+690)x = -20x^2 + 690x \end{aligned}\] Die Gewinnfunktion lautet: \[\begin{aligned} \pi &=& R(x) - C(x)\\ &=& -20x^2 + 690x -(0.08831x^3-7.6893x^2+255x+5900)\\ &=& -0.08831x^3 -12.3107x^2 + 435x - 5900 \end{aligned}\] Nun bilden wir die erste Ableitung der Gewinnfunktion und erhalten folgende quadratische Funktion: \[\begin{aligned} \pi' = -0.26493x^2 -24.6214x + 435 = 0 \end{aligned}\] Mit Hilfe der quadratischen Formel berechnen wir nun das Angebot, bei dem der Monopolist den maximalen Gewinn erzielt. \[\begin{aligned} x_1,_2 &=& \frac{-B \pm \sqrt{(B^2-4AC)}}{2A}\\ x_1,_2 &=& \frac{-(-24.6214) \pm \sqrt{(-24.6214)^2-(4\cdot (-0.26493)\cdot 435)}}{2\cdot (-0.26493)}\\ x_1 &=& 15.186082\\ x_2 &=& -108.121575 \end{aligned}\] Die Funktion besitzt kritische Punkte in \(x_1 = 15.186082\) und \(x_2= -108.121575\). Um sicherzugehen, dass die positive Lösung tatsächlich ein Maximum ist, berechnen wir die zweite Ableitung an der Stelle \(x_1 = 15.186082\): \[\begin{aligned} \pi''(x) = -0.52986x - 24.6214 \\ \pi''(15.186082) = -32.667898 < 0. \end{aligned}\] Daher handelt es sich tatsächlich um ein Maximum.
Bei einem Angebot von \(x = 15.19\) Stück erzielt der Monopolist maximalen Gewinn.
Ein Chemieunternehmen besitzt aufgrund eines Patents ein Monopol auf ein spezielles Pflanzenschutzmittel. Die Nachfragefunktion nach diesem Produkt lautet bei einem Preis \(p\): \[\begin{aligned} D(p):~x &=& -0.5p+880 \end{aligned}\] An fixen Kosten fallen bei der Produktion 4900 GE an, die variablen Kosten sind durch die Funktion gegeben: \[\begin{aligned} V(x) &=& 0.02321x^3-1.423x^2+286x \end{aligned}\] Welchen Gewinn erzielt das Unternehmen, wenn es seinen Erlös maximiert?
Um den Erlös zu maximieren, könnten wir die Erlösfunktion so wie bisher als Funktion des Preises darstellen. Da wir aber den dabei erzielten Gewinn auch noch ausrechnen wollen, gehen wir gleich von Beginn an zu der Darstellung als Funktion der abgesetzten Menge über. Wir berechnen die inverse Nachfragefunktion, also die Funktion, die uns zu jeder Menge \(x\) den Preis \(p\) angibt, der zum vollständigen Verkauf der Menge \(x\) führt: \[\begin{aligned} D(p):~x &=& -0.5p + 880\\ p&=& -2x + 1760 \end{aligned}\] Damit nimmt die Erlösfunktion die folgende Form an: \[\begin{aligned} R(x) = p\cdot x = (-2x+1760)x = -2x^2 + 1760x \end{aligned}\] Zunächst ist die Menge zu berechnen, bei der der Erlös maximiert wird. Daher bilden wir die erste Ableitung der Erlösfunktion, setzen diese Null und erhalten den kritschen Punkt der Erlösfunktion: \[\begin{aligned} R'(x) & = & -4 x + 1760 = 0\\ x & = & \frac{1760}{4} = 440 \end{aligned}\] Um zu überprüfen, ob der kritische Punkt \(x = 440\) ein Maximum ist, berechnen wir die zweite Ableitung der Erlösfunktion an der Stelle \(x = 440\): \[\begin{aligned} R''(x) & = & -4 < 0 \end{aligned}\] Damit nimmt die Erlösfunktion an der Stelle \(x_{max} = 440\) ME ein Maximum an.
Uns interessiert jedoch der Gewinn, der mit dieser Menge erzielt wird. Die Gewinnfunktion lautet \[\begin{aligned} \pi(x) &=& R(x) - C(x)\\ &=& -2x^2 + 1760x - (0.02321x^3-1.423x^2 + 286x + 4900)\\ &=& -2\cdot 440^2 + 1760\cdot 440 - (0.02321\cdot 440^3-1.423\cdot 440^2 + 286\cdot 440 + 4900) \\ &=& -1445167.84 \end{aligned}\] Daraus ergibt sich \(\pi(440) = -1445167.84\) GE.
Ein Chemieunternehmen besitzt aufgrund eines Patents ein Monopol auf ein spezielles Pflanzenschutzmittel. Die Nachfragefunktion nach diesem Produkt lautet bei einem Preis \(p\): \[\begin{aligned} D(p):~x &=& -0.125p+800 \end{aligned}\] An fixen Kosten fallen bei der Produktion 5800 GE an, die variablen Kosten sind durch die Funktion gegeben: \[\begin{aligned} V(x) &=& 0.06151x^3-7.0087x^2+109x \end{aligned}\] Welchen Gewinn erzielt das Unternehmen, wenn es seinen Erlös maximiert?
Um den Erlös zu maximieren, könnten wir die Erlösfunktion so wie bisher als Funktion des Preises darstellen. Da wir aber den dabei erzielten Gewinn auch noch ausrechnen wollen, gehen wir gleich von Beginn an zu der Darstellung als Funktion der abgesetzten Menge über. Wir berechnen die inverse Nachfragefunktion, also die Funktion, die uns zu jeder Menge \(x\) den Preis \(p\) angibt, der zum vollständigen Verkauf der Menge \(x\) führt: \[\begin{aligned} D(p):~x &=& -0.125p + 800\\ p&=& -8x + 6400 \end{aligned}\] Damit nimmt die Erlösfunktion die folgende Form an: \[\begin{aligned} R(x) = p\cdot x = (-8x+6400)x = -8x^2 + 6400x \end{aligned}\] Zunächst ist die Menge zu berechnen, bei der der Erlös maximiert wird. Daher bilden wir die erste Ableitung der Erlösfunktion, setzen diese Null und erhalten den kritschen Punkt der Erlösfunktion: \[\begin{aligned} R'(x) & = & -16 x + 6400 = 0\\ x & = & \frac{6400}{16} = 400 \end{aligned}\] Um zu überprüfen, ob der kritische Punkt \(x = 400\) ein Maximum ist, berechnen wir die zweite Ableitung der Erlösfunktion an der Stelle \(x = 400\): \[\begin{aligned} R''(x) & = & -16 < 0 \end{aligned}\] Damit nimmt die Erlösfunktion an der Stelle \(x_{max} = 400\) ME ein Maximum an.
Uns interessiert jedoch der Gewinn, der mit dieser Menge erzielt wird. Die Gewinnfunktion lautet \[\begin{aligned} \pi(x) &=& R(x) - C(x)\\ &=& -8x^2 + 6400x - (0.06151x^3-7.0087x^2 + 109x + 5800)\\ &=& -8\cdot 400^2 + 6400\cdot 400 - (0.06151\cdot 400^3-7.0087\cdot 400^2 + 109\cdot 400 + 5800) \\ &=& -1584648 \end{aligned}\] Daraus ergibt sich \(\pi(400) = -1584648.00\) GE.
Ein Chemieunternehmen besitzt aufgrund eines Patents ein Monopol auf ein spezielles Pflanzenschutzmittel. Die Nachfragefunktion nach diesem Produkt lautet bei einem Preis \(p\): \[\begin{aligned} D(p):~x &=& -0.04p+910 \end{aligned}\] An fixen Kosten fallen bei der Produktion 1200 GE an, die variablen Kosten sind durch die Funktion gegeben: \[\begin{aligned} V(x) &=& 0.06301x^3-5.5099x^2+140x \end{aligned}\] Welchen Gewinn erzielt das Unternehmen, wenn es seinen Erlös maximiert?
Um den Erlös zu maximieren, könnten wir die Erlösfunktion so wie bisher als Funktion des Preises darstellen. Da wir aber den dabei erzielten Gewinn auch noch ausrechnen wollen, gehen wir gleich von Beginn an zu der Darstellung als Funktion der abgesetzten Menge über. Wir berechnen die inverse Nachfragefunktion, also die Funktion, die uns zu jeder Menge \(x\) den Preis \(p\) angibt, der zum vollständigen Verkauf der Menge \(x\) führt: \[\begin{aligned} D(p):~x &=& -0.04p + 910\\ p&=& -25x + 22750 \end{aligned}\] Damit nimmt die Erlösfunktion die folgende Form an: \[\begin{aligned} R(x) = p\cdot x = (-25x+22750)x = -25x^2 + 22750x \end{aligned}\] Zunächst ist die Menge zu berechnen, bei der der Erlös maximiert wird. Daher bilden wir die erste Ableitung der Erlösfunktion, setzen diese Null und erhalten den kritschen Punkt der Erlösfunktion: \[\begin{aligned} R'(x) & = & -50 x + 22750 = 0\\ x & = & \frac{22750}{50} = 455 \end{aligned}\] Um zu überprüfen, ob der kritische Punkt \(x = 455\) ein Maximum ist, berechnen wir die zweite Ableitung der Erlösfunktion an der Stelle \(x = 455\): \[\begin{aligned} R''(x) & = & -50 < 0 \end{aligned}\] Damit nimmt die Erlösfunktion an der Stelle \(x_{max} = 455\) ME ein Maximum an.
Uns interessiert jedoch der Gewinn, der mit dieser Menge erzielt wird. Die Gewinnfunktion lautet \[\begin{aligned} \pi(x) &=& R(x) - C(x)\\ &=& -25x^2 + 22750x - (0.06301x^3-5.5099x^2 + 140x + 1200)\\ &=& -25\cdot 455^2 + 22750\cdot 455 - (0.06301\cdot 455^3-5.5099\cdot 455^2 + 140\cdot 455 + 1200) \\ &=& 316098.45875 \end{aligned}\] Daraus ergibt sich \(\pi(455) = 316098.46\) GE.
Ein Unternehmen, das Bleistifte herstellt, überlegt in einen Markt für spezielle Lidstifte einzusteigen. Da der Produktionsprozess von Lidstiften ähnlich zu dem von Bleistiften ist, glaubt das Unternehmen, sich gegen den bisher einzigen Hersteller von Lidstiften durchsetzen zu können. Dafür ist es zunächst essentiell, die Produktionskosten dieses Monopolisten zu schätzen.
Das Unternehmen kennt die Nachfragefunktion für die speziellen Lidstifte: \[\begin{aligned} q(p) = 1434-18 p \end{aligned}\]
Außerdem weiß das Unternehmen, dass dem Monopolisten konstante Stückkosten von \(k\) GE pro Lidstift anfallen. Dabei verlangt der Monopolist einen Preis von \(p = 65\) GE pro Lidstift. Man kann davon ausgehen, dass der Monopolist zu diesem Preis seinen Gewinn maximiert. Wie hoch sind die konstanten Stückkosten des Monopolisten?
Die Gewinnfunktion des Monopolisten in Abhängigkeit des Preises ist gegeben durch \[\begin{aligned} \pi(p) & = & q(p)\cdot p - \left(q(p) \cdot k + d \right) \\ & = & 1434 \cdot p - 18 \cdot p^2 - \left(1434 \cdot k - 18 \cdot p \cdot k + d \right) \end{aligned}\] Da der Monopolist den gewinnmaximierenden Preis wählt, muss die Bedingung erster Ordnung erfüllt sein: \[\begin{aligned} \pi'(p) = 1434 - 2 \cdot 18 \cdot p + 18 \cdot k \stackrel{!}{=} 0 \end{aligned}\] Damit es sich um ein Maximum handelt, muss die zweite Ableitung \(\pi''(p) < 0\) sein. \[\begin{aligned} \pi''(p) = -2 \cdot 18 \Rightarrow \pi''(p) < 0 \end{aligned}\] Nun können wir den gewinnmaximierenden Preis für die Lidstifte einsetzen und \(k\) freistellen: \[\begin{aligned} \pi'(65) = 1434 - 2 \cdot 18 \cdot 65 + 18 \stackrel{!}{=} 0 \Rightarrow k = 50.333333 \end{aligned}\] Die konstanten Stückkosten \(k\) des Monopolisten betragen gerundet \(50.33\) GE.
Ein Unternehmen, das Bleistifte herstellt, überlegt in einen Markt für spezielle Lidstifte einzusteigen. Da der Produktionsprozess von Lidstiften ähnlich zu dem von Bleistiften ist, glaubt das Unternehmen, sich gegen den bisher einzigen Hersteller von Lidstiften durchsetzen zu können. Dafür ist es zunächst essentiell, die Produktionskosten dieses Monopolisten zu schätzen.
Das Unternehmen kennt die Nachfragefunktion für die speziellen Lidstifte: \[\begin{aligned} q(p) = 1056-18 p \end{aligned}\]
Außerdem weiß das Unternehmen, dass dem Monopolisten konstante Stückkosten von \(k\) GE pro Lidstift anfallen. Dabei verlangt der Monopolist einen Preis von \(p = 35\) GE pro Lidstift. Man kann davon ausgehen, dass der Monopolist zu diesem Preis seinen Gewinn maximiert. Wie hoch sind die konstanten Stückkosten des Monopolisten?
Die Gewinnfunktion des Monopolisten in Abhängigkeit des Preises ist gegeben durch \[\begin{aligned} \pi(p) & = & q(p)\cdot p - \left(q(p) \cdot k + d \right) \\ & = & 1056 \cdot p - 18 \cdot p^2 - \left(1056 \cdot k - 18 \cdot p \cdot k + d \right) \end{aligned}\] Da der Monopolist den gewinnmaximierenden Preis wählt, muss die Bedingung erster Ordnung erfüllt sein: \[\begin{aligned} \pi'(p) = 1056 - 2 \cdot 18 \cdot p + 18 \cdot k \stackrel{!}{=} 0 \end{aligned}\] Damit es sich um ein Maximum handelt, muss die zweite Ableitung \(\pi''(p) < 0\) sein. \[\begin{aligned} \pi''(p) = -2 \cdot 18 \Rightarrow \pi''(p) < 0 \end{aligned}\] Nun können wir den gewinnmaximierenden Preis für die Lidstifte einsetzen und \(k\) freistellen: \[\begin{aligned} \pi'(35) = 1056 - 2 \cdot 18 \cdot 35 + 18 \stackrel{!}{=} 0 \Rightarrow k = 11.333333 \end{aligned}\] Die konstanten Stückkosten \(k\) des Monopolisten betragen gerundet \(11.33\) GE.
Ein Unternehmen, das Bleistifte herstellt, überlegt in einen Markt für spezielle Lidstifte einzusteigen. Da der Produktionsprozess von Lidstiften ähnlich zu dem von Bleistiften ist, glaubt das Unternehmen, sich gegen den bisher einzigen Hersteller von Lidstiften durchsetzen zu können. Dafür ist es zunächst essentiell, die Produktionskosten dieses Monopolisten zu schätzen.
Das Unternehmen kennt die Nachfragefunktion für die speziellen Lidstifte: \[\begin{aligned} q(p) = 1395-23 p \end{aligned}\]
Außerdem weiß das Unternehmen, dass dem Monopolisten konstante Stückkosten von \(k\) GE pro Lidstift anfallen. Dabei verlangt der Monopolist einen Preis von \(p = 37\) GE pro Lidstift. Man kann davon ausgehen, dass der Monopolist zu diesem Preis seinen Gewinn maximiert. Wie hoch sind die konstanten Stückkosten des Monopolisten?
Die Gewinnfunktion des Monopolisten in Abhängigkeit des Preises ist gegeben durch \[\begin{aligned} \pi(p) & = & q(p)\cdot p - \left(q(p) \cdot k + d \right) \\ & = & 1395 \cdot p - 23 \cdot p^2 - \left(1395 \cdot k - 23 \cdot p \cdot k + d \right) \end{aligned}\] Da der Monopolist den gewinnmaximierenden Preis wählt, muss die Bedingung erster Ordnung erfüllt sein: \[\begin{aligned} \pi'(p) = 1395 - 2 \cdot 23 \cdot p + 23 \cdot k \stackrel{!}{=} 0 \end{aligned}\] Damit es sich um ein Maximum handelt, muss die zweite Ableitung \(\pi''(p) < 0\) sein. \[\begin{aligned} \pi''(p) = -2 \cdot 23 \Rightarrow \pi''(p) < 0 \end{aligned}\] Nun können wir den gewinnmaximierenden Preis für die Lidstifte einsetzen und \(k\) freistellen: \[\begin{aligned} \pi'(37) = 1395 - 2 \cdot 23 \cdot 37 + 23 \stackrel{!}{=} 0 \Rightarrow k = 13.347826 \end{aligned}\] Die konstanten Stückkosten \(k\) des Monopolisten betragen gerundet \(13.35\) GE.