9 Bivariate Wahrscheinlichkeitsrechnung

9.1 Vorbemerkung

In diesem Kapitel kehren wir kurz zur Wahrscheinlichkeitsrechnung zurück und definieren den Begriff der Kovarianz von Zufallsgrößen. Damit werden wir in die Lage versetzt, die Variabilität von Linearkombinationen von Zufallsgrößen zu beurteilen, wenn diese nicht unabhängig sind, sondern eine spezielle Art der Kopplung besteht, man diese Korrelation. Der Fall der Unabhängigkeit wurde bereits in Kapitel 5 ausführlich behandelt.

Das Konzept der Kovarianz verbinden wir mit den in Kapitel 8 entwickelten Ideen zur Optimierung unter Nebenbedingungen, um schließlich ein außerordentlich spannendes Thema aus der modernen Finanzmathematik zu diskutieren, die Optimierung eines Portfolios. Dieses Problem ist uns schon in Abschnitt 5.3.5 begegnet, allerdings waren wir dort beschränkt auf Finanzanlagen, deren Renditen unabhängige Zufallsgrößen sind.

9.2 Die Kovarianz von Zufallsgrößen

Es seien \(X\) und \(Y\) zwei Zufallsgrößen mit den Erwartungswerten \(\mu_x,\,\mu_y\) und den Varianzen \(\sigma_x^2,\,\sigma_y^2\). Wir wollen nun den Erwartungswert und die Varianz einer Linearkombination \(aX+bY\) berechnen.

Aus Satz 5.40 wissen wir, dass \[ \begin{gathered} E(aX+bY)=aE(X)+bE(Y). \end{gathered} \] Diese Formel ist immer richtig (sofern die Erwartungswerte existieren). Im Fall der Varianz ist die Sache nicht so einfach. Wir wissen aus Satz 5.56, dass für unabhängige Zufallsgrößen die Formel \[ \begin{gathered} V(aX+bY)=a^2V(X)+b^2V(Y) \end{gathered} \] gilt. Nun stellt sich aber die Frage, wie man die Varianz einer Linearkombination berechnen kann, wenn die Zufallsgrößen nicht unabhängig sind. Für die Beantwortung dieser Frage benötigen wir einen neuen Begriff.

Definition 9.1 Unter der Kovarianz von zwei Zufallsgrößen \(X\) und \(Y\) versteht man \[ \begin{gathered} \Cov(X,Y)=\sigma_{xy}=E((X-\mu_x)(Y-\mu_y)). \end{gathered} \]

Zunächst ist die Kovarianz nur eine Abkürzung für jenen Term, der bei der Berechnung der Varianz einer Summe von Zufallsgrößen auftritt (siehe Begründung von Satz 5.56): \[ \begin{gathered} V(X+Y)=V(X)+2\Cov(X,Y)+V(Y)= \sigma_x^2+2\sigma_{xy}+\sigma_y^2. \end{gathered} \tag{9.1}\] Die Kovarianz hat aber durchaus auch eine eigenständige Bedeutung.

Die Kovarianz hängt eng mit dem Begriff der Varianz zusammen. Es ist ja offensichtlich, dass \(\Cov(X,X)=V(X)\): Die Kovarianz einer Zufallsgröße mit sich selbst ist identisch mit der Varianz der Zufallsgröße.

Auch eine weitere Eigenschaft hat die Kovarianz mit der Varianz gemeinsam: Wenn eine der beiden Zufallsgrößen konstant ist, dann ist die Kovarianz gleich Null. Das ist ganz einfach zu verstehen. Wenn \(X\) konstant ist, dann ist \(X=\mu_x\) und daher \(X-\mu_x=0\). Folglich ist \[ \begin{gathered} \Cov(X,Y)=E(0\cdot(Y-\mu_y))=E(0)=0. \end{gathered} \]

Besonderes wichtig für das Weitere ist die folgende Tatsache.

Satz 9.2 Wenn die beiden Zufallsgrößen \(X\) und \(Y\) stochastisch unabhängig sind, dann ist die Kovarianz von \(X\) und \(Y\) gleich Null, also \(\Cov(X,Y)=0\).

Begründung: Wir wissen aus dem Multiplikationssatz für Erwartungswerte (Satz 5.48), dass der Erwartungswert des Produkts von unabhängigen Zufallsgrößen gleich dem Produkt der Erwartungswerte ist. Also gilt \[ \begin{gathered} \Cov(X,Y)=E((X-\mu_x)(Y-\mu_y))=E(X-\mu_x)E(Y-\mu_y) \end{gathered} \] Jeder der beiden Faktoren ist Null, denn \[ \begin{gathered} E(X-\mu_x)=E(X)-\mu_x=0,\quad E(Y-\mu_y)=E(Y)-\mu_y=0, \end{gathered} \] und daher ist \(\Cov(X,Y)=0\). □

Wenn die Kovarianz ungleich Null ist, dann bedeutet das also, dass die Zufallsgrößen gekoppelt sind.

Die Kovarianz ist eine Maßzahl für eine bestimmte Art der Koppelung von Zufallsgrößen. Man nennt diese Art der Koppelung Korrelation.

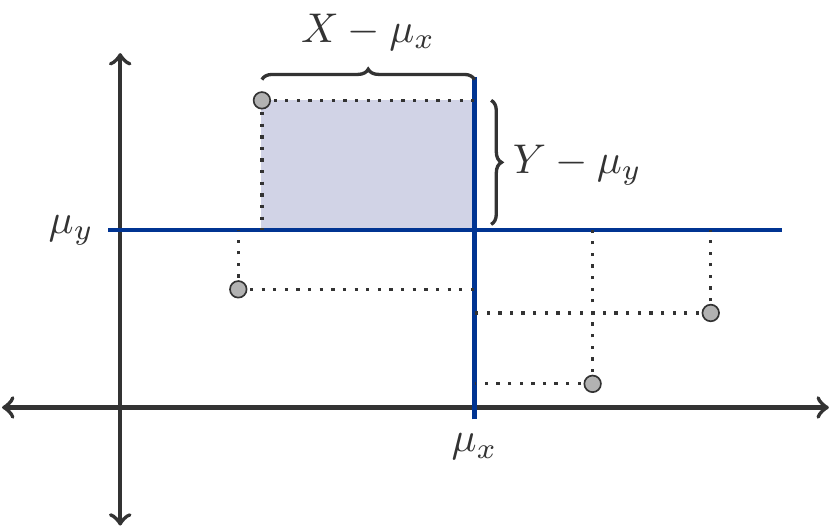
Bemerkung 9.3 (Interpretation der Korrelation) Um zu verstehen, was Korrelation bedeutet, muss man das Produkt \[ \begin{gathered} (X-\mu_x)(Y-\mu_y) \end{gathered} \] verstehen. Dieses Produkt ist positiv, wenn entweder beide Faktoren positiv oder beide negativ sind. Das bedeutet aber, dass beide Zufallsgrößen gleichzeitig einen überdurchschnittlichen (\(X>\mu_x\) und \(Y>\mu_y\)) oder beide gleichzeitig einen unterdurchschnittlichen Wert annehmen (\(X<\mu_x\) und \(Y<\mu_y\)). Das Produkt ist negativ, wenn genau einer der Faktoren negativ ist, somit wenn \(X\) überdurchschnittlich und \(Y\) unterdurchschnittlich ist (\(X>\mu_x\) und \(Y<\mu_y\)), oder umgekehrt.

Wenn \(\Cov(X,Y)>0\) (positive Korrelation), dann überwiegen die Realisationen, bei denen \(X\) und \(Y\) in der gleichen Richtung von ihrem Erwartungswert abweichen (hinsichtlich Häufigkeit und Ausmaß).

Diese Situation ist illustriert in Abbildung 9.1. Die Produkte \((X-\mu_x)(Y-\mu_y)\) sind nichts anderes als Flächeninhalte (mit Vorzeichen), der durch die Punkte \((X,Y)\) und \(\mu_x,\mu_y\) definierten Rechtecke.

Bei positiver Korrelation liegen die Wertepaare \((X,Y)\) überwiegend im ersten bzw. dritten Quadranten bezüglich ihres gemeinsamen Schwerpunkts \((\mu_x,\mu_y)\). Die Rechtecke in diesen Quadranten haben positiven Inhalt.

Wenn jedoch \(\Cov(X,Y)<0\) (negative Korrelation), dann überwiegen die Realisationen, bei denen \(X\) und \(Y\) in unterschiedlicher Richtung von ihrem Erwartungswert abweichen (hinsichtlich Häufigkeit und Ausmaß).

Bei negativer Korrelation liegen daher die Wertepaare \((X,Y)\) überwiegend im zweiten bzw. vierten Quadranten bezüglich ihres gemeinsamen Schwerpunkts \((\mu_x,\mu_y)\). Die Rechtecke in diesen Quadranten haben negativen Inhalt, siehe Abbildung 9.2.

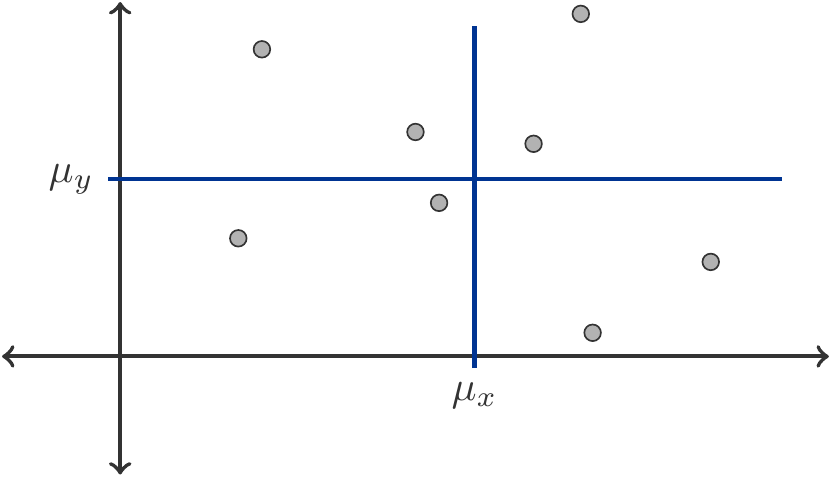
Sind hingegen \(X\) und \(Y\) unabhängig, dann wirkt es sich auf \(Y\) nicht aus, ob \(X\) über- oder unterdurchschnittliche Werte annimmt, \(\Cov(X,Y)=0\), siehe Abbildung 9.3. Die Wertepaare \((X,Y)\) sind bezüglich des gemeinsamen Schwerpunkts \((\mu_x, \mu_y)\) ganz regellos verteilt.

Abbildung 9.3: Unkorrelierte Zufallsgrößen

Definition 9.4 Zwei Zufallsgrößen \(X, Y\) heißen korreliert, wenn \(\Cov(X,Y)\not=0\). Sie heißen positiv korreliert, wenn \(\Cov(X,Y)>0\), und negativ korreliert, wenn \(\Cov(X,Y)<0\).

Musteraufgabe 9.5 Es seien \(X,Y\) Zufallsgrößen mit \(\sigma_x^2=3\), \(\sigma_y^2=5\) und \(V(X+Y)=9\). Man berechne \(\sigma_{xy}\).

Lösung: Mit Hilfe von (9.1) \[ \begin{aligned} V(X+Y)&=\sigma_x^2+2\sigma_{xy}+\sigma_y^2\\[1ex] 9 &= 3+2\sigma_{xy}+5\\[2ex] \implies \sigma_{xy}&=1/2. \end{aligned} \] Die beiden Zufallsgrößen sind also positiv korreliert. □

Die Kovarianz hat einige Eigenschaften, die beim Rechnen nützlich sind. Wir fassen diese Eigenschaften übersichtlich zusammen. Es seien \(X,Y\) und \(Z\) Zufallsgrößen. Dann gilt:

Regel 1: \(\begin{array}{l} \Cov(X,X)=V(X) \end{array}\)

Regel 2: \(\begin{array}{l} \Cov(X,Y)=\Cov(Y,X) \end{array}\)

Regel 3: \(\begin{array}[t]{llcl} \Cov(X+Y,Z)&=\Cov(X,Z)&+&\Cov(Y,Z),\\ \Cov(X,Y+Z)&=\Cov(X,Y)&+&\Cov(X,Z) \end{array}\)

Regel 4: \(\begin{array}[t]{ll} \Cov(aX,Y)&=a\Cov(X,Y),\\ \Cov(X,bY)&=b\Cov(X,Y). \end{array}\)

Es ist nicht schwierig, diese Eigenschaften aus der Definition der Kovarianz und den Eigenschaften des Erwartungswerts abzuleiten.

Für die Varianz einer Linearkombination \(aX+bY\) von Zufallsgrößen ergibt sich damit eine allgemeine Formel.

Satz 9.6 Es seien \(X\) und \(Y\) Zufallsgrößen, dann: \[ \begin{aligned} V(aX+bY)&=a^2V(X)+2ab\,\Cov(X,Y)+b^2V(Y)\\ &=a^2\sigma_x^2+2ab\sigma_{xy}+b^2\sigma_y^2. \end{aligned} \]

Begründung: Zur Begründung setzen wir \(U=aX, W=bY\). Dann ist, wie wir wissen, \[ \begin{gathered} V(aX+bY)=V(U+W)=V(U)+2\Cov(U,W)+V(W) \end{gathered} \] Aus den Eigenschaften der Varianz folgt, dass \(V(U)=a^2V(X)\) und \(V(W)=b^2V(Y)\). Darüber hinaus gilt nach Regel 4: \[ \begin{gathered} \Cov(U,W)=\Cov(aX,bY)=ab\,\Cov(X,Y). \end{gathered} \] □

Musteraufgabe 9.7 Es seien \(X,Y\) Zufallsgrößen mit \(\sigma_x^2=3\), \(\sigma_y^2=5\) und \(\sigma_{xy}=-2\). Man berechne \(V(X-2Y)\).

Lösung: Mit Hilfe von Satz 9.6: \[ \begin{aligned} V(X-2Y)&=1^2\sigma_x^2-4\sigma_{xy}+4\sigma_y^2\\ &=1^2\cdot 3-4\cdot(-2)+4\cdot5=31. \end{aligned} \] □

Musteraufgabe 9.8 Es seien \(X,Y\) Zufallsgrößen mit \(\sigma_x^2=3\), \(\sigma_y^2=5\) und \(\sigma_{xy}=-2\).

Man bestimme \(\Cov(X-2,Y+5)\).

Lösung: Es ist \[ \begin{aligned} \Cov(X-2,Y+5)&=\Cov(X-2,Y)+\Cov(X-2,5). \end{aligned} \] Der zweite Term rechts ist Null, denn \(\Cov(c,X)=\Cov(X,c)=0\), wenn \(c\) konstant ist. Daraus folgt \[ \begin{aligned} \Cov(X-2,Y+5)&=\Cov(X-2,Y)\\[1ex] &=\Cov(X,Y)+\Cov(-2,Y) =\Cov(X,Y)=-2. \end{aligned} \] □

Musteraufgabe 9.9 Es seien \(X,Y\) Zufallsgrößen mit \(\sigma_x^2=3\), \(\sigma_y^2=5\) und \(\sigma_{xy}=-2\).

Man bestimme \(\Cov(X+Y,2X)\).

Lösung: \[ \begin{aligned} \Cov(X+Y,2X)&=\Cov(X,2X) +\Cov(Y,2X)\\[1ex] &=2\Cov(X,X)+2\Cov(Y,X)\\[1ex] &=2V(X)+2\Cov(X,Y)\\[1ex] &=2\cdot 3+2\cdot(-2)=2. \end{aligned} \] □

Musteraufgabe 9.10 Es seien \(X,Y\) Zufallsgrößen mit \(\sigma_x^2=3\), \(\sigma_y^2=5\) und \(\sigma_{xy}=-2\).

Man bestimme \(\Cov(3X-Y,X+2Y)\).

Lösung: \[ \begin{aligned} \Cov(3X-Y,&X+2Y)=\Cov(3X-Y,X) +2\Cov(3X-Y,Y)\\[1ex] &=3\Cov(X,X)-\Cov(Y,X)+6\Cov(X,Y) -2\Cov(Y,Y)\\[1ex] &=3\sigma_x^2+5\sigma_{xy}-2\sigma_y^2\\[1ex] &=9-10-10=-11. \end{aligned} \] □

Musteraufgabe 9.11 Es seien \(X,Y\) Zufallsgrößen mit \(\sigma_x^2=3\), \(\sigma_y^2=5\) und \(\sigma_{xy}=-2\).

Man bestimme \(\Cov(X-5Y+3,7X-2)\).

Lösung: \[ \begin{aligned} \Cov(X-5Y+3,7X-2)& =\Cov(X-5Y,7X)\\[1ex] & =\Cov(X,7X)-5\Cov(Y,7X)\\[1ex] & = 7V(X)-35\Cov(X,Y)\\[1ex] & = 21+70=91. \end{aligned} \] □

Die nächsten beiden Aufgaben leiten über zu unserem letzten Thema.

Musteraufgabe 9.12 Es seien \(X,Y\) die Renditen zweier Wertpapiere, wobei \(\sigma_x^2=0.2\), \(\sigma_y^2=0.3\) und \(\sigma_{xy}=-0.2\). Man berechne die Varianz der Rendite jenes Portfolios, das zu 30 Prozent aus \(X\) und zu 70 Prozent aus \(Y\) besteht.

Lösung: Es sei \(P=0.3X+0.7Y\) die gemeinsame Rendite des Portfolios. \[ \begin{gathered} V(0.3X+0.7Y)=0.3^2\cdot 0.2+2\cdot 0.3\cdot 0.7\cdot (-0.2) +0.7^2\cdot 0.3 =0.081\,. \end{gathered} \] □

Musteraufgabe 9.13 Es seien \(X,Y\) die Renditen zweier Wertpapiere, wobei \(\sigma_x^2=0.2\), \(\sigma_y^2=0.3\) und \(\sigma_{xy}=-0.2\). Man ermittle das Portfolio, dessen Rendite die kleinste Varianz besitzt. Wie hoch ist die Varianz der Rendite des optimalen Portfolios?

Lösung: Die Prozentsätze des in die beiden Wertpapiere investierten Kapitals seien \(\alpha\) und \(1-\alpha\). Die Rendite des Portfolios \(P=\alpha X+(1-\alpha)Y\) hat die Varianz \[ \begin{aligned} V(P)&=V(\alpha X+(1-\alpha)Y)\\ &=\alpha^2\cdot 0.2+2\alpha(1-\alpha)(-0.2)+(1-\alpha)^2\cdot 0.3\\ &=0.9\alpha^2-\alpha +0.3. \end{aligned} \] Die Varianz ist eine quadratische Funktion von \(\alpha\) und hat ihr Minimum bei \(\alpha=0.5556\). Daher lautet das optimale Portfolio \((0.5556,0.4444)\). Die Varianz beträgt \(V(P)=0.0222\). □

9.3 Portfolio-Optimierung

Der Begriff Portfolio wurde bereits in Abschnitt 5.3.5 im Detail erörtert. Die Leserinnen und Leser sind eingeladen zur Orientierung diese Seiten nochmals zu überfliegen, um den Ausführungen hier leichter folgen zu können.

Die entscheidenden Gedanken nochmals in aller Kürze:

Ein Portfolio ist eine Entscheidung über die prozentuelle Aufteilung des verfügbaren Kapitals auf zwei oder mehr Wertpapiere.
Die Renditen dieser Papiere sind in aller Regel Zufallsgrößen mit einer Varianz.
Die Varianz der gemeinsamen Rendite gilt als Maß für das Kapitalrisiko, das mit dem Portfolio verbunden ist.
Je größer die Varianz der gemeinsamen Rendite, umso riskanter ist die Anlage.

Es ist daher naheliegend, die Kapitalanteile der Papiere am Portfolio zu Entscheidungsvariablen eines Optimierungsproblems zu machen.

Bei der Lösung dieser Optimierungsaufgabe beschränken wir uns auf Portfolios, die aus maximal drei Wertpapieren zusammengesetzt sind. Diese Beschränkung hat rein handwerkliche Gründe und kann mit wenig mehr Aufwand gelockert werden.

Ein Investor habe die Möglichkeit, sein Kapital entweder festverzinslich mit garantiertem Zinssatz \(r\) zu veranlagen, oder es in eines oder beide von zwei weiteren Wertpapieren zu investieren. Der Investor bildet ein Portfolio aus diesen drei Wertpapieren, wobei er die Prozentsätze \(\alpha_0\), \(\alpha_1\) und \(\alpha_2\) seines verfügbaren Kapitals investiert.

Es seien \(X_0\), \(X_1\) und \(X_2\) die Renditen (für eine Periode) der drei Wertpapiere. Die Erwartungswerte und Varianzen der Renditen seien \[ \begin{gathered} \begin{array}{l@{\quad}l} E(X_0)=r& V(X_0)=0,\\ E(X_1)=\mu_1 & V(X_1)=\sigma_1^2,\\ E(X_2)=\mu_2 & V(X_2)=\sigma_2^2. \end{array} \end{gathered} \] Die Kovarianz betrage \(\Cov(X_1,X_2)=\sigma_{12}\). Die Kovarianzen von \(X_0\) mit \(X_1\) und \(X_2\) sind Null, denn \(X_0\) ist eine Konstante.

Ein Portfolio ist definiert durch drei Zahlen \(\alpha_0\), \(\alpha_1\) und \(\alpha_2\) mit der Eigenschaft \[ \begin{gathered} \alpha_0+\alpha_1+\alpha_2=1. \end{gathered} \] Diese drei Zahlen entsprechen den Prozentsätzen, nach denen das verfügbare Startkapital des Investors auf die drei Wertpapiere aufgeteilt wird. Sie sind die Kapitalanteile der Papiere am Portfolio.

Bemerkung 9.14 (Ein Auswahlproblem) Es ist wichtig, auf folgende Punkte gesondert hinzuweisen:

Wir nehmen an, dass in den Portfolios, die wir betrachten, ein gewisser Teil des Kapitals festverzinslich und damit risikofrei veranlagt werden kann. Risikofrei bedeutet, dass die Varianz der Rendite dieser Anlage Null ist.
Die Entscheidung, was die anderen beiden Papiere des Portfolios sind, ist schon im Vorfeld gefallen. Investorinnen haben sich also ausreichend informiert und beschlossen, in welche Papiere sie investieren werden.
Unsere Aufgabe wird darin bestehen, die optimalen Kapitalanteile \(\alpha_0,\alpha_1\) und \(\alpha_2\) zu ermitteln.

Das erwähnte Auswahlproblem ist nicht einfach zu lösen. Zweifellos wird dabei aber die Kovarianz der Renditen der Papiere eine Rolle spielen. Wenn \(\Cov(X_1,X_2)>0\), so steht dahinter eine durchaus risikofreudige Strategie, denn wenn \(X_1\) zunimmt, dann hat auch \(X_2\) die Tendenz zuzunehmen. Das gilt aber auch in umgekehrter Richtung: eine Abschwächung in \(X_1\) geht tendenziell mit einer Abschwächung von \(X_2\) einher. Das typische Beispiel wäre, in Aktien eines Autoherstellers und in solche eines Autozulieferers zu investieren.

Umgekehrt, werden die beiden nicht festverzinslichen Papiere so ausgewählt, dass \(\Cov(X_1,X_2)<0\), dann kommt hier eine eher defensive Strategie zum Ausdruck. Negative Kovarianz der Renditen bedeutet, dass sich die Renditen tendenziell in entgegengesetzte Richtung bewegen. Eine Abschwächung in \(X_1\) wird kompensiert durch ein Stärkerwerden von \(X_2\) und umgekehrt. Beispielsweise könnte jemand in Kohlekraftwerksbetreiber investieren und alternativ in Unternehmen, die Energie aus erneuerbaren Quellen bereitstellen.

Bemerkung 9.15 (Negative Kapitalanteile) Die Prozentsätze, durch die ein Portfolio definiert ist, können auch negativ sein! Ein negativer Prozentsatz bedeutet, dass der Investor zu Beginn der Periode Kapital ausleiht und dieses am Ende der Periode einschließlich der Rendite des betreffenden Wertpapiers zurückzahlen muss. Mit anderen Worten, man macht ganz bewusst eine Verbindlichkeit zu einem Bestandteil des Portfolios.

Das Startkapital des Investors betrage \(K\).

Wenn das Portfolio durch \((-0.2,0.6,0.6)\) definiert ist, bedeutet das, dass der Investor \(0.2K\) zusätzlich zum Festzinssatz \(r\) als Kredit aufnimmt und damit Wertpapiere 1 und 2 im Wert von jeweils \(0.6K\) finanziert. Teil seines Portfolios ist somit die Verbindlichkeit, am Ende den Betrag \(0.2K(1+r)\) zurückzuzahlen.

Der Investor verpflichtet sich also, am Ende der Periode ein Sparbuch mit dem Guthaben \(0.2K(1+r)\) abzuliefern und erhält als Preis für diese Verpflichtung den Betrag \(0.2K\) bereits am Beginn der Periode. Man nennt diesen Vorgang Short Selling.

Wenn das Portfolio durch \((0.6,-0.2,0.6)\) definiert ist, bedeutet das, dass der Investor den Betrag \(0.2K\) zusätzlich dadurch aufnimmt, dass er sich verpflichtet, am Ende der Periode den Betrag \(0.2K(1+X_1)\) (gleichsam das Wertpapier 1 in diesem Umfang) abzuliefern. Der Investor könnte etwa am Beginn der Periode Wertpapiere zum Tageskurs \(0.2K\) leihen und sie an der Börse verkaufen. Am Ende der Periode müssen diese Papiere an der Börse zum aktuellen Kurs \(0.2K(1+X_1)\) zurückgekauft werden.

Short Selling ist dann sinnvoll, wenn man das dadurch aufgenommene zusätzliche Kapital besser investieren kann, als die Kosten der eingegangenen Verbindlichkeit betragen.

Die Rendite des Portfolios ist die Zufallsgröße \[ \begin{aligned} P&=\alpha_0 r+\alpha_1 X_1+ \alpha_2 X_2\\ &=(1-\alpha_1-\alpha_2)r+\alpha_1 X_1+ \alpha_2 X_2\\ &=r+\alpha_1(X_1-r)+\alpha_2(X_2-r). \end{aligned} \]

Wir berechnen nun Erwartungswert und Varianz der Rendite Portfolios. Die Rendite des Portfolios hat den Erwartungswert \[ \begin{gathered} E(P)=r+\alpha_1(\mu_1-r)+\alpha_2(\mu_2-r). \end{gathered} \] Die Differenzen \(\mu_1-r\) und \(\mu_2-r\) nennt man auch die Risikoprämien der beiden Papiere.

Die Varianz der Rendite berechnen wir mit Hilfe von Satz 9.6: \[ \begin{gathered} V(P)=\alpha_1^2\sigma_1^2+2\alpha_1\alpha_2\sigma_{12}+ \alpha_2^2\sigma_2^2. \end{gathered} \] Der Investor ist daran interessiert, sein Portfolio, also die Prozentsätze \(\alpha_1\) und \(\alpha_2\), so zu wählen, dass er eine möglichst große Rendite (Erwartungswert) bei möglichst kleinem Risiko (Varianz) erzielt. Diese beiden Anlageziele stehen jedoch in Konkurrenz zueinander, daher muss ein geeigneter Kompromiss gefunden werden.

Zwei mögliche Strategien sind:

Minimiere das Risiko unter der Nebenbedingung einer vorgegebenen
erwarteten Rendite - die defensive Strategie.
Maximiere die erwartete Rendite unter der Nebenbedingung eines vorgegebenen Risikos - die offensive Strategie.

Beide Aufgabenstellungen führen auf ein Optimierungsproblem unter Nebenbedingungen, das wir mit der Methode von Lagrange (siehe Abschnitt 8.8.2) lösen können.

Zwischen diesen beiden Varianten gibt es natürlich alle möglichen Zwischenformen, je nach Risikoaffinität der Anleger.

Risikominimierung

Musteraufgabe 9.16 Ein Investor stellt ein Portfolio aus drei Wertpapieren zusammen, von denen das erste festverzinslich ist mit dem Zinssatz 7 Prozent. Die beiden anderen Wertpapiere haben Renditen mit den Erwartungswerten 0.08 und 0.12, und den Varianzen 0.04 und 0.09. Die Kovarianz der Renditen der beiden Wertpapiere beträgt 0.036.

Der Investor möchte ein Portfolio mit erwarteter Rendite 0.1 und minimaler Varianz erhalten.

Wie muss das Startkapital des Investors auf die drei Wertpapiere aufgeteilt werden?
Wie groß ist die Varianz der Rendite des optimalen Portfolios?

Lösung: Die Zielfunktion, die minimiert werden soll, ist die Varianz des Portfolios und lautet \[ \begin{gathered} C(\alpha_1,\alpha_2)=V(P)=0.04\alpha_1^2+0.072\alpha_1\alpha_2+ 0.09\alpha_2^2\to\min. \end{gathered} \] Die Nebenbedingung besagt, dass der Erwartungswert der Rendite des Portfolios \(0.1\) betragen soll. Das bedeutet \[ \begin{aligned} F(\alpha_1,\alpha_2)&=E(P)\\ &=0.07+\alpha_1(0.08-0.07)+\alpha_2(0.12-0.07)=0.1, \end{aligned} \] oder vereinfacht \[ \begin{gathered} 0.01\alpha_1+0.05\alpha_2=0.03\,.\qquad \mbox{(A)} \end{gathered} \] Unter dieser Nebenbedingung soll die Zielfunktion minimiert werden. Wir wenden die Methode der Lagrange-Multiplikatoren an. Die Lagrange-Funktion lautet \[ \begin{gathered} \begin{array}{rcl} L(\alpha_1,\alpha_2)&=&C(\alpha_1,\alpha_2)-\lambda(F(\alpha_1,\alpha_2)-0.1)\\ &=&0.04\alpha_1^2+0.072\alpha_1\alpha_2+0.09\alpha_2^2\\ & &-\lambda(0.01\alpha_1+0.05\alpha_2-0.03). \end{array} \end{gathered} \] Um einen kritischen Punkt zu finden, bilden wir die partiellen Ableitungen und setzen diese gleich Null: \[ \begin{gathered} \begin{array}{rcrcrcrcc} L_1'&=&0.080\alpha_1&+&0.072\alpha_2&-&0.01\lambda&=&0\\ L_2'&=&0.072\alpha_1&+&0.180\alpha_2&-&0.05\lambda&=&0 \end{array} \end{gathered} \] Diese Gleichungen führen auf die Lösung \(\alpha_1=-0.1953\lambda\) und \(\alpha_2=0.3559\lambda\). Nun muss noch \(\lambda\) so gewählt werden, dass die Nebenbedingung erfüllt ist. Zu diesem Zweck setzen wir die Ausdrücke für \(\alpha_1\) und \(\alpha_2\) in die Nebenbedingung (A) ein. Das führt auf \[ \begin{gathered} \lambda=\frac{0.03}{-0.1953\cdot0.01+ 0.3559\cdot 0.05}=1.8937\,. \end{gathered} \] Also lautet die Lösung \[ \begin{gathered} \alpha_1=-0.3698,\; \alpha_2=0.6740, \end{gathered} \] und das Portfolio ist durch \((0.6958,-0.3699,0.6740)\) gegeben. Wir gehen auf short in Wertpapier 1, das zugehörige Risiko ist die Varianz der Rendite dieses Portfolios \(V(P)=0.0284\). □

Bemerkung 9.17 (Sensitivität des Resultats) Die Leserinnen und Leser erinnern sich sicherlich noch an unsere ökonomische Deutung des Lagrange-Multiplikators in Abschnitt 8.8.3 Dort sahen wir, dass \(\lambda\) die Änderungsrate der Optimums ist bezüglich der in der Nebenbedingung festgeschriebenen Beschränkung.

In unserem Beispiel ist \(\lambda\simeq 1.9\), die Beschränkung in der Nebenbedingung ist das Renditeziel \(q=0.1\). Angenommen, wir erhöhen das Renditeziel auf 11%. Dann wird der Wert des Optimums der Zielfunktion \(V^\ast(0.1)\), das Risiko also, zunehmen. Näherungsweise wird diese Zunahme sein: \[ \begin{gathered} V^\ast(0.11)-V^\ast(0.1)\approx 0.01\cdot \lambda=0.019. \end{gathered} \] Das bedeutet, dass \[ \begin{gathered} V^\ast(0.11)\approx 0.0284+0.019=0.0474.\qquad \mbox{(D)} \end{gathered} \] Wir erwarten daher eine beträchtliche Erhöhung des Anlagerisikos!

Die Leser sind eingeladen, diese Vorhersage zu überprüfen. Erneute Rechnung, nun mit Renditeziel 11%, zeigt, dass das Ergebnis sehr sensibel reagiert. Nun erhalten wir ein Portfolio mit verringertem risikofreien Anteil \(\alpha_0\) und deutlich erhöhtem Short-Anteil \(\alpha_1\) in Papier 1. Diese zusätzlichen Mittel gehen in Wertpapier 2, dessen Kapitalanteil \(\alpha_2\) um 25% zunimmt: \[ \begin{gathered} \alpha_0=0.5945,\quad \alpha_1=-0.4932, \quad \alpha_2=0.8987\,. \end{gathered} \] Die Varianz der Rendite und damit das Risiko erhöhen sich auf \(V^\ast(0.11)=0.0505\). Die Vorhersage (D) ist somit recht genau.

Musteraufgabe 9.18 Eine Investorin stellt ein Portfolio aus drei Wertpapieren zusammen, von denen das erste festverzinslich ist mit dem Zinssatz 4 Prozent. Die beiden anderen Wertpapiere haben Renditen mit den Erwartungswerten 0.06 und 0.1, und den Varianzen 0.04 und 0.09. Die Kovarianz der Renditen der beiden Wertpapiere beträgt -0.018.

Die Investorin möchte ein Portfolio mit erwarteter Rendite 0.08 und minimaler Varianz erhalten.

Wie muss das Startkapital der Investorin auf die drei Wertpapiere aufgeteilt werden?
Wie groß ist die Varianz der Rendite des optimalen Portfolios?

Lösung: Wir fassen uns nun kürzer als beim vorangehenden Beispiel. Die Zielfunktion, die minimiert werden soll, lautet \[ \begin{gathered} V(P)=0.04\alpha_1^2-0.036\alpha_1\alpha_2+ 0.09\alpha_2^2\to\min. \end{gathered} \] Sie soll unter der linearen Nebenbedingung \[ \begin{gathered} E(P)=0.04+\alpha_1(0.06-0.04)+\alpha_2(0.1-0.04)= 0.08, \end{gathered} \] dh. \[ \begin{gathered} 0.02\alpha_1+0.06\alpha_2= 0.04, \end{gathered} \] minimiert werden. Die Lagrange-Funktion ist \[ \begin{gathered} \begin{array}{rcl} L(\alpha_1,\alpha_2) &=& 0.04\alpha_1^2-0.036\alpha_1\alpha_2+0.09\alpha_2^2\\ &&-\lambda(0.02\alpha_1+0.06\alpha_2-0.04). \end{array} \end{gathered} \] Die partiellen Ableitungen werden gleich Null gesetzt: \[ \begin{aligned} \begin{array}{rcrcrcc} 0.080\alpha_1&-&0.036\alpha_2&-&0.02\lambda&=&0\\ -0.036\alpha_1&+&0.180\alpha_2&-&0.06\lambda&=&0 \end{array} \end{aligned} \]

Diese Gleichungen führen auf die Lösung \(\alpha_1=0.4396\lambda\) und \(\alpha_2=0.4212\lambda\). Nun muss noch \(\lambda\) so gewählt werden, dass die Nebenbedingung erfüllt ist. Das führt auf \[ \begin{gathered} \lambda=\frac{0.04}{0.4396\cdot0.02+ 0.4212\cdot 0.06}=1.1742\,. \end{gathered} \] Also lautet die Lösung \[ \begin{gathered} \alpha_1=0.5161,\; \alpha_2=0.4946\,. \end{gathered} \] und das Portfolio ist \((-0.0107,0.5161,0.4946)\). Die Varianz der Rendite dieses Portfolios beträgt \(V(P)=0.0235\). Nun haben wir Short Selling in der risikofreien Anlage. Die Interpretation des Lagrange-Multiplikators bleibt den Lesern überlassen. □

Renditemaximierung

Musteraufgabe 9.19 Ein Investor stellt ein Portfolio aus drei Wertpapieren zusammen, von denen das erste festverzinslich ist mit dem Zinssatz 7 Prozent. Die beiden anderen Wertpapiere haben Renditen mit den Erwartungswerten 0.08 und 0.12, und den Varianzen 0.04 und 0.09. Die Kovarianz der Rendite der beiden Wertpapiere beträgt -0.018.

Der Investor möchte ein Portfolio mit Varianz der Rendite 0.01 und maximaler erwarteter Rendite erhalten.

Wie muss das Startkapital des Investors auf die drei Wertpapiere aufgeteilt werden?
Wie groß ist die erwartete Rendite des optimalen Portfolios?

Lösung: Die Zielfunktion, die maximiert werden soll, ist der Erwartungswert der Rendite des Portfolios. Sie lautet \[ \begin{aligned} C(\alpha_1,\alpha_2)=E(P)&=0.07+\alpha_1(0.08-0.07)+\alpha_2 (0.12-0.07)\\ &=0.07+0.01\alpha_1+0.05\alpha_2. \end{aligned} \] Die Nebenbedingung besagt, dass die Varianz des Portfolios \(0.01\) betragen soll. Das bedeutet \[ \begin{gathered} F(\alpha_1,\alpha_2)=V(P)=0.04\alpha_1^2 -0.036\alpha_1\alpha_2+ 0.09\alpha_2^2= 0.01\,. \end{gathered} \] Unter dieser Nebenbedingung soll die Zielfunktion maximiert werden. Wir wenden die Methode der Lagrange-Multiplikatoren an. Die Lagrange-Funktion ist \[ \begin{gathered} \begin{array}{rcl} L(\alpha_1,\alpha_2)&=& C(\alpha_1,\alpha_2)-\lambda(F(\alpha_1,\alpha_2)-0.01)\\ &=& 0.07+0.01\alpha_1+0.05\alpha_2\\ &&-\lambda( 0.04\alpha_1^2 -0.036\alpha_1\alpha_2+ 0.09\alpha_2^2-0.01). \end{array} \end{gathered} \] Um einen kritischen Punkt zu finden, bilden wir die partiellen Ableitungen und setzen diese gleich Null: \[ \begin{gathered} \begin{array}{ccrcrcrcc} L_1'&=&0.01&-& 0.080\lambda\alpha_1 &+&0.036\lambda\alpha_2&=&0\\ L_2'&=&0.05 &+&0.036\lambda\alpha_1&-&0.180\lambda\alpha_2&=&0 \end{array} \end{gathered} \] Diese Gleichungen führen auf die Lösung \(\alpha_1=0.2747/\lambda\) und \(\alpha_2=0.3327/\lambda\). Nun muss noch \(\lambda\) so gewählt werden, dass die Nebenbedingung erfüllt ist. Zu diesem Zweck setzen wir die Ausdrücke für \(\alpha_1\) und \(\alpha_2\) in die Nebenbedingung ein. Das führt auf \(\lambda^2=0.969\) und daher \(\lambda_{1,2}=\pm \sqrt{0.969}=\pm 0.9845\).

Wir haben nun zwei kritische Punkte, je nach Vorzeichen des Multiplikators. Dazu berechnen wir auch gleich den Wert der Zielfunktion, die erwartete Rendite: \[ \begin{gathered} \lambda_1=0.9845, \; \alpha_1=0.2791, \; \alpha_2=0.3380, \; C(\alpha_1,\alpha_2)=0.0897 \end{gathered} \] und \[ \begin{gathered} \lambda_2=-0.9845, \; \alpha_1=-0.2791, \; \alpha_2=-0.3380, \; C(\alpha_1,\alpha_2)=0.0503 \end{gathered} \] Da wir die maximale erwartete Rendite suchen, nehmen wir die erste der beiden Lösungen, jene mit dem positiven Lagrange-Multiplikator. Die ergibt immerhin eine erwartete Rendite von ca. 9% bei festverzinslichem Kapitalanteil \(\alpha_0=0.3829\).

Übrigens, wir hätten die Entscheidung zwischen \(\lambda_1\) und \(\lambda_2\) auch mit einem Plausibilitätsargument herbeiführen können. Wieder kommt die ökonomische Deutung des Lagrange-Multiplikators ins Spiel: wenn wir das in der Nebenbedingung festgeschriebene Risikoziel von \(0.01\) erhöhen, dann erwarten wir auch höheren mittleren Ertrag im Optimum. Daher muss der optimale Wert des Multiplikators positiv sein. □

Musteraufgabe 9.20 Eine Investorin stellt ein Portfolio aus drei Wertpapieren zusammen, von denen das erste festverzinslich ist mit dem Zinssatz 3 Prozent. Die beiden anderen Wertpapiere haben Renditen mit den Erwartungswerten 0.05 und 0.12, und den Varianzen 0.04 und 0.07. Die Kovarianz der Rendite der beiden Wertpapiere beträgt 0.02115.

Die Investorin möchte ein Portfolio mit der Varianz der Rendite 0.02 und maximaler erwarteter Rendite erhalten.

Wie muss das Startkapital des Investors auf die drei Wertpapiere aufgeteilt werden?
Wie groß ist die erwartete Rendite des optimalen Portfolios?

Lösung: Die Zielfunktion, die minimiert werden soll, lautet \[ \begin{aligned} E(P)&=0.03+\alpha_1(0.05-0.03)+\alpha_2 (0.12-0.03)\\ &=0.03+0.02\alpha_1+0.09\alpha_2. \end{aligned} \] Sie soll unter der Nebenbedingung \[ \begin{gathered} V(P)=0.04\alpha_1^2+ 0.0423\alpha_1\alpha_2+ 0.07\alpha_2^2= 0.02 \end{gathered} \] maximiert werden. Die Lagrange-Funktion lautet \[ \begin{gathered} \begin{array}{rcl} L(\alpha_1,\alpha_2)&=& 0.03+0.02\alpha_1+0.09\alpha_2\\ &&-\lambda( 0.04\alpha_1^2+ 0.0423\alpha_1\alpha_2+ 0.07\alpha_2^2-0.02) \end{array} \end{gathered} \] Bilden der partiellen Ableitungen nach \(\alpha_1\) und \(\alpha_2\) liefert die Gleichungen: \[ \begin{gathered} \begin{array}{rcrcrcc} 0.02&-&0.0800\lambda\alpha_1&-& 0.0423\lambda\alpha_2&=&0\\ 0.09&-& 0.0423\lambda\alpha_1&-&0.1400\lambda\alpha_2&=&0 \end{array} \end{gathered} \] Diese Gleichungen führen auf die Lösung \(\alpha_1=-0.1070/\lambda\) und \(\alpha_2=0.6752/\lambda\). Nun muss noch \(\lambda\) so gewählt werden, dass die Nebenbedingung erfüllt ist. Das führt auf \(\lambda^2=1.4657\) oder \(\lambda=\pm \sqrt{1.4657}\).

Erneut haben wir es mit zwei Lösungen zu tun, von denen eine das Maximum und die andere das Minimum ist. Wie im letzten Beispiel ausgeführt kann nur der positive Wert \(\lambda=\sqrt{1.4657}\) des Lagrange-Multiplikators das Maximum liefern. Somit erhalten wir die Kapitalanteile des optimalen Portfolios als: \[ \begin{gathered} \alpha_0=0.5307,\quad \alpha_1=-0.0884,\quad \alpha_2=0.5577. \end{gathered} \] Die optimale erwartete Rendite beträgt \(0.0784\). □

9.4 Weitere Übungsaufgaben

Es seien \(X\) und \(Y\) Zufallsgrößen mit \(\sigma_x^2=20, \sigma_y^2=13\) und \(\sigma_{xy}=13\). Berechnen Sie \(V(9 X -3 Y)\).

Lösung: \(V(9 X -3 Y)=1035\)
Es seien \(X\) und \(Y\) Zufallsgrößen mit \(\sigma_x^2=19, \sigma_y^2=18\) und \(V(9 X +8 Y)=4419\). Berechnen Sie \(\sigma_{xy}\).

Lösung: \(\sigma_{xy}=12\)
Es seien \(X\) und \(Y\) Zufallsgrößen mit \(\sigma_x^2=18, \sigma_y^2=10\) und \(\sigma_{xy}=-11\). Berechnen Sie \(\Cov(X-14, Y+10)\).

Lösung: \(\Cov(X-14,Y+10)=-11\)
Es seien \(X\) und \(Y\) Zufallsgrößen mit \(\sigma_x^2=13, \sigma_y^2=17\) und \(\sigma_{xy}=-12\). Berechnen Sie \(\Cov(X+Y,-10X)\).

Lösung: \(\Cov(X+Y,-10X)=-10\)
Es seien \(X\) und \(Y\) Zufallsgrößen mit \(\sigma_x^2=11, \sigma_y^2=10\) und \(\sigma_{xy}=-7\). Berechnen Sie mit diesen Angaben \(\Cov(14X-Y,X+9Y)\).

Lösung: \(\Cov(14X-Y,X+9Y)=-811\)
Es seien \(X\) und \(Y\) die Renditen zweier Wertpapiere, wobei \(\sigma_x^2=0.1, \sigma_y^2=0.11\) und \(\sigma_{xy}=-0.07\). Berechnen Sie die Varianz der Rendite jenes Portfolios, das zu 67 Prozent aus Wertpapier 1 und zu 33 Prozent aus Wertpapier 2 besteht.

Lösung: \(V(R)=0.0259\)
Es seien \(X\) und \(Y\) die Renditen zweier Wertpapiere, wobei \(\sigma_x^2=0.34, \sigma_y^2=0.42\) und \(\sigma_{12}=0.28\). Wie groß ist der prozentuelle Anteil der Wertpapiere an jenem Portfolio, dessen Rendite die kleinste Varianz aufweist?

Lösung: 70 %, 30 %
Eine Investorin stellt ein Portfolio aus drei Wertpapieren zusammen, von denen das erste festverzinslich ist mit Zinssatz \(5.5\) Prozent. Die beiden anderen Wertpapiere haben Renditen mit den Erwartungswerten \(0.105\) und \(0.14\), und den Varianzen \(0.06\) und \(0.09\). Die Kovarianz der Renditen beträgt \(0.04\). Die Investorin möchte ein Portfolio mit erwarteter Rendite \(0.14\) und minimaler Varianz erhalten. Berechnen Sie die Kapitalanteile des optimalen Portfolios.

Lösung: \(V=0.0862, \alpha_0=-0.1209,\alpha_1=0.2936,\alpha_2=0.8273\)
Ein Investor stellt ein Portfolio aus drei Wertpapieren zusammen, von denen das erste festverzinslich ist mit Zinssatz \(3\) Prozent. Die beiden anderen Wertpapiere haben Renditen mit den Erwartungswerten \(0.125\) und \(0.09\), und den Varianzen \(0.10\) und \(0.03\). Die Kovarianz der Renditen beträgt \(0.03\). Ein Investor möchte ein Portfolio mit erwarteter Rendite \(0.10\) und minimaler Varianz erhalten. Wie groß ist die Varianz des optimalen Portfolios?

Lösung: \(V=0.0356, \alpha_0=-0.0182,\alpha_1= 0.2545,\alpha_2= 0.7636\)
Eine Investorin stellt ein Portfolio aus drei Wertpapieren zusammen, von denen das erste festverzinslich ist mit Zinssatz \(7\) Prozent. Die beiden anderen Wertpapiere haben Renditen mit den Erwartungswerten \(0.105\) und \(0.125\), und den Varianzen \(0.05\) und \(0.04\). Die Kovarianz der Renditen beträgt \(0.03\). Die Investorin möchte ein Portfolio mit der Varianz \(0.02\) und maximaler erwarteter Rendite erhalten. Berechnen Sie die Kapitalanteile des optimalen Portfolios.

Lösung: \(E(R)=0.1093, \alpha_0= 0.3284,\alpha_1= -0.1158,\alpha_2= 0.7874\)
Ein Investor stellt ein Portfolio aus drei Wertpapieren zusammen, von denen das erste festverzinslich ist mit Zinssatz \(5\) Prozent. Die beiden anderen Wertpapiere haben Renditen mit den Erwartungswerten \(0.12\) und \(0.09\), und den Varianzen \(0.08\) und \(0.03\). Die Kovarianz der Renditen beträgt \(-0.03\). Ein Investor möchte ein Portfolio mit der Varianz \(0.015\) und maximaler Rendite erhalten. Wie groß ist die erwartete Rendite des optimalen Portfolios?

Lösung: \(E(R)=0.1166, \alpha_0= -0.2921,\alpha_1= 0.4958,\alpha_2= 0.7963\)