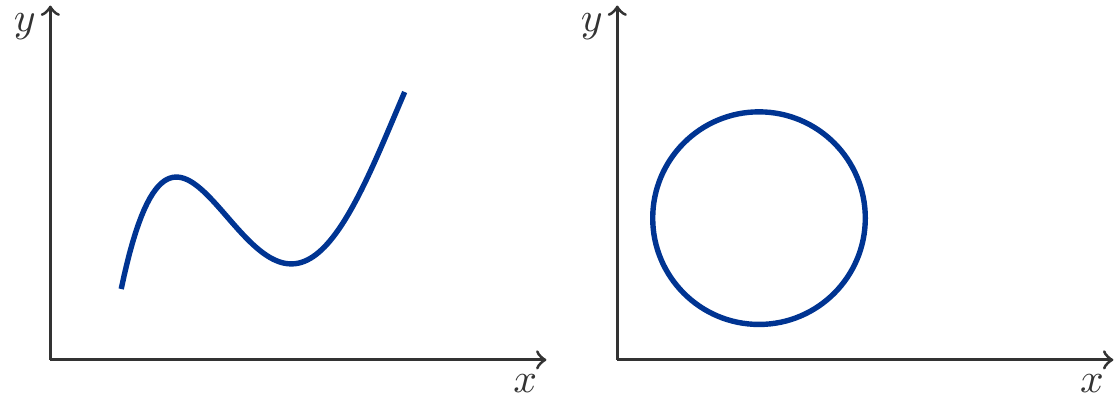
8 Analysis von Funktionen mit zwei Variablen
\[ \definecolor{dgray}{rgb}{0.3,0.3,0.3} \definecolor{lgray}{rgb}{0.85,0.85,0.85} \]
8.1 Vorbemerkungen
In diesem Kapitel werden wir die im Kapitel 3 präsentierten Methoden der Differentialrechnung weiterentwickeln und erweitern auf Funktionen mit zwei Variablen.
Was erwartet uns?
Die uns vertrauten Formeln für das Ableiten von Potenzen, Logarithmen und Exponentialfunktionen gelten weiterhin. Das Gleiche gilt für die uns nicht weniger vertrauten Regeln wie Produktregel, Kettenregel, usw.
Was ändert sich?
Unsere Funktionen haben nun zwei unabhängige Variable. Während die Graphen von Funktionen in einer Variablen Kurven in der Ebene waren, sind die Graphen nun im allgemeinen mehr oder weniger kompliziert geformte Flächen im 3-dimensionalen Raum. Wir haben also geänderte geometrische Verhältnisse, und denen müssen wir in geeigneter Weise Rechnung tragen.
Daher ist es nur folgerichtig, wenn wir damit beginnen einige wichtige geometrische Grundlagen zu diskutieren.
8.2 Geometrische Grundlagen
Wir werden die unabhängigen Variablen der Funktionen, die wir betrachten, meist mit \(x\) und \(y\) bezeichnen. Geometrisch entsprechen sie den Koordinaten eines Punktes \(\mathbf x=\left(\begin{array}{c}x\\y\end{array}\right)\) in der \((x,y)-\)Ebene, dem \(\mathbb R^2\). Während bei Funktionen in einer Variablen diese ihre Werte in einem ein-dimensionalen Intervall annehmen, kann \(\mathbf x\) nun irgendein Punkt einer Teilmenge \(M\subset\mathbb R^2\) sein.
Doch werden wir häufig und mit gutem Grund vereinbaren, dass die Koordinaten \(x\) und \(y\) des Punktes \(\mathbf x\) nicht voneinander unabhängig sind, sondern gemeinsam variieren. Damit meinen wir, dass \(x\) und \(y\) Funktionen einer reellen Variablen \(t\) sind: \[ \begin{gathered} x=g_1(t),\quad y=g_2(t),\qquad t\in \mathbb R. \end{gathered} \tag{8.1}\] Wenn nun die Werte von \(t\) ein Intervall durchlaufen, dann beschreiben \(x\) und \(y\) eine Kurve in der Ebene, man nennt diese Kurve einen Pfad, der parameterisiert wird durch die Gleichungen (8.1).
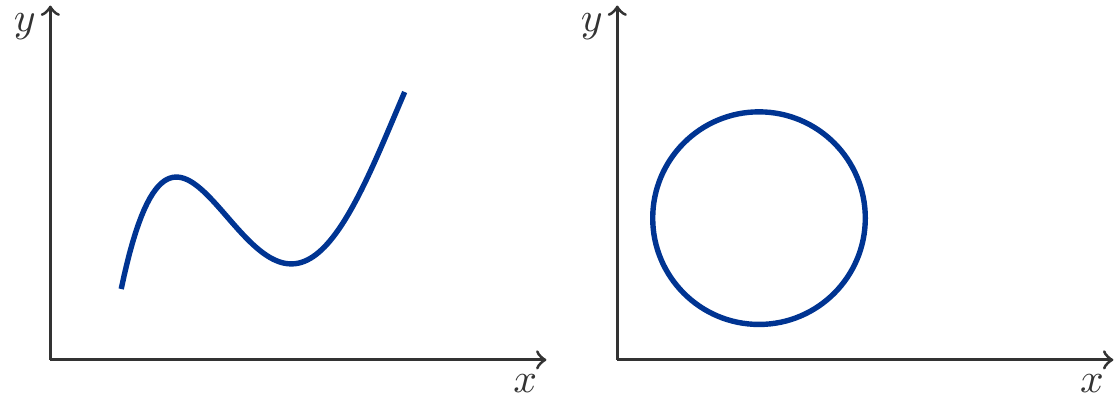
In Abbildung 8.1 sind zwei Pfade zu sehen. Im linken Bild sieht man einen Pfad, der durch ein Polynom 3. Grades, \[ \begin{gathered} x=t,\quad y=a_0+a_1t+a_2t^2+a_3t^3,\qquad u\le t\le v \end{gathered} \] erzeugt wird, während im zweiten Beispiel der Pfad eine geschlossene Kurve (ein Kreis) ist, erzeugt durch \[ \begin{gathered} x=a+r\cos t,\quad y=b+r\sin t,\qquad -\pi\le t\le \pi. \end{gathered} \] Hier sind \(a,b\) die Koordinaten des Mittelpunkts und \(r\) sein Radius1.
Selbstverständlich sind wir in der Hauptsache an solchen Pfaden interessiert, die besonders einfache Gestalt haben. Damit meinen wir Pfade, die im \(\mathbb R^2\) geradlinig verlaufen.

Solche Geraden können wir durch lineare Gleichungen beschreiben, die Leser erinnern sich gewiss an Kapitel 1.
Achsenparallele Geraden beschreiben wir durch die Gleichungen: \[ \begin{gathered} \begin{array}{ccccl} x&=&a &&\text{parallel zur $y$-Achse}\\ y&=&b &&\text{parallel zur $x$-Achse} \end{array}, \end{gathered} \] Geraden in allgemeiner Lage durch die Gleichung \(ax+by=c\).
Es wird sich als vorteilhaft erweisen, für diese drei Fälle eine gemeinsame Beschreibung zu haben. Dazu verwenden wir die Idee des Vektors.
Vektoren sind uns erstmals in Kapitel 6 begegnet. Dort definierten wir sie als Listen von Zahlen. Wir bleiben bei dieser Definition, schränken sie aber ein auf Listen der Länge 2.
Vektoren \(\mathbf a,\;\mathbf b\in\mathbb R^2\) können geometrisch als Punkte oder als Verschiebungen (symbolisiert durch Pfeile) interpretiert werden (siehe Abbildung 8.3).
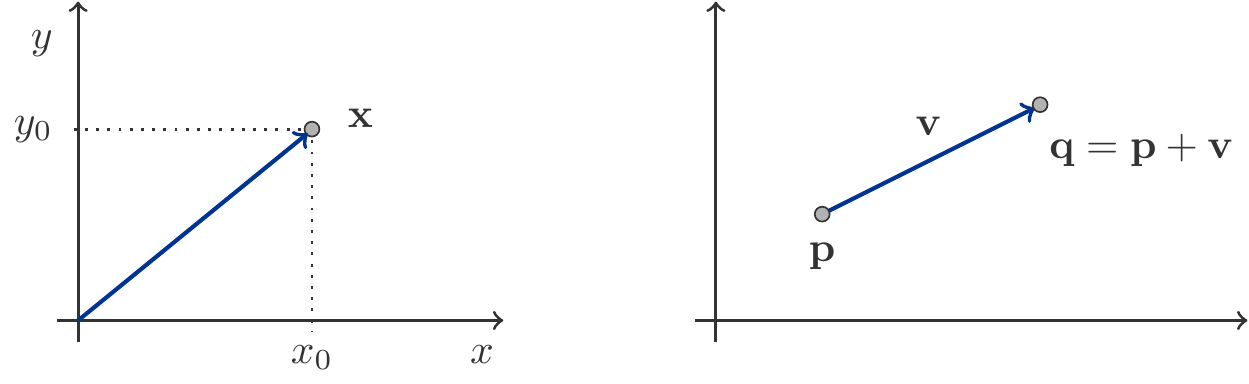
Rechenoperationen mit Vektoren entsprechen ebenfalls geometrischen Vorgängen.
Addiert man zu einem Punktvektor \(\mathbf p\) einen Verschiebungsvektor \(\mathbf v\), dann erhält man als Ergebnis \(\mathbf q=\mathbf p+\mathbf v\) jenen Punktvektor, der durch die Verschiebung \(\mathbf v\) des Punktes \(\mathbf p\) entsteht: \[ \begin{gathered} \text{Anfangspunkt} + \text{Verschiebung}=\text{Endpunkt}\\ \mathbf p+\mathbf v=\mathbf q \end{gathered} \]
Entsprechend ist \(\mathbf v=\mathbf q-\mathbf p\) der Verschiebungsvektor von \(\mathbf p\) nach \(\mathbf q\): \[ \begin{gathered} \text{Verschiebung}=\text{Endpunkt}-\text{Anfangspunkt}\\ \mathbf v = \mathbf q-\mathbf p \end{gathered} \]
So gesehen kann jeder Punktvektor \(\mathbf x\) auch als Verschiebungsvektor vom Ursprung \(\boldsymbol{0}\) des Koordinatensystems zum Punkt \(\mathbf x\) gedeutet werden.
Die Multiplikation eines Vektors mit einer Zahl interpretiert man geometrisch am einfachsten über die Deutung des Vektors als Verschiebungsvektor.
Es sei \(\mathbf w=\lambda\mathbf v\). Der Faktor \(\lambda\) verändert die Verschiebung \(\mathbf v\) in zweierlei Hinsicht. Das Vorzeichen von \(\lambda\) bestimmt die Richtung:
Ist \(\lambda>0\), dann ist \(\mathbf w\) eine Verschiebung in die gleiche Richtung wie \(\mathbf w\).
Ist \(\lambda<0\), dann ist \(\mathbf w\) eine Verschiebung in die entgegengesetzte Richtung von \(\mathbf v\).
Der Absolutbetrag von \(\lambda\) bestimmt die Veränderung der Länge des Verschiebungsvektors.
Zwei Vektoren, die sich nur um einen Faktor unterscheiden, nennt man proportional. In der Interpretation als Verschiebungsvektoren bedeutet proportional also nichts anderes als parallel.
8.2.1 Parameterform einer Geraden
Geraden im \(\mathbb R^2\) können wir angeben durch einen Punkt \(\mathbf a\) und einen Verschiebungsvektor \(\mathbf v\). Genauer:
Definition 8.1 (Parameterform einer Geraden) Man nennt \[ \begin{gathered} g=\{\mathbf x : \mathbf x = \mathbf a + t\mathbf v, t\in\mathbb R\},\quad \mathbf x=\left(\begin{array}{c}x\\y\end{array}\right), \mathbf v\ne \boldsymbol{0} \end{gathered} \] die Parameterform einer Geraden.
Dabei sind: \[ \begin{array}{ccl} g &=& \text{Menge aller Punkte $x$ auf der Geraden}\\ \mathbf x &=& \text{Punkt auf $g$,} \\ \mathbf a &=& \text{Anfangspunkt,}\\ \mathbf v &=& \text{Verschiebungsvektor.} \end{array} \]
Bemerkung 8.2 Es gibt natürlich unendlich viele verschiedene Parameterformen ein und derselben Geraden, je nachdem, welche Punkte \(\mathbf a\) und Verschiebungsvektoren \(\mathbf v\) man benutzt. Die entstehende Punktmenge ist dabei immer die gleiche.
Man kann sich die Unterschiede zwischen verschiedenen Parameterformen einer Geraden auf folgende Weise veranschaulichen.
Stellen wir uns vor, wir beginnen eine Fahrt entlang der Geraden \(g\), wobei \(\mathbf a\) der Startpunkt ist und der Parameter \(t\) die verstrichene Zeit bezeichnet. Wenn eine Zeitspanne der Länge \(t=1\) verstreicht, verändert sich unsere Position auf der Geraden um den Verschiebungsvektor \(\mathbf v\). Deshalb nennt man den Verschiebungsvektor \(\mathbf v\) auch den Geschwindigkeitsvektor.
Eine Parameterform \(\mathbf x=\mathbf a+t\mathbf v\) einer Geraden ist also eine gleichförmige Bewegung entlang der Geraden, die im Punkt \(\mathbf a\) startet und mit dem Geschwindkeitsvektor \(\mathbf v\) fortschreitet.
Musteraufgabe 8.3 Man finde eine Parameterform der Geraden mit der Gleichung \(3x+y=15\).
Lösung: Wir verschaffen uns zwei Punkte der Geraden, zum Beispiel dadurch, dass wir einmal \(x=0\) und einmal \(y=0\) setzen: \[ \begin{gathered} \mathbf a=\left(\begin{array}{r}0\\15\end{array}\right),\qquad \mathbf b=\left(\begin{array}{r}5\\0\end{array}\right). \end{gathered} \] Daher ist der zugehörige Verschiebungsvektor: \[ \begin{gathered} \mathbf v=\mathbf b-\mathbf a=\left(\begin{array}{r}5\\-15 \end{array}\right), \end{gathered} \] und eine Parameterform der Geraden lautet daher: \[ \begin{gathered} g=\left\{\mathbf x=\mathbf a+t\mathbf v= \left(\begin{array}{r}0\\15\end{array}\right) +t \left(\begin{array}{r}5\\-15 \end{array}\right):t\in\mathbb R\right\}. \end{gathered} \] □
Geraden parallel zu den Koordinatenachsen werden eine wichtige Rolle spielen, ihre Parameterformen sind leicht zu finden: wir wählen den Verschiebungsvektor \(\mathbf v\) parallel zu den Koordinatenachsen: \[ \begin{gathered} \begin{array}{rclcl} \mathbf x&=&\mathbf a+t\left(\begin{array}{c}1\\0\end{array}\right) &&\parallel \text{ zur $x$-Achse}\\[10pt] \mathbf x&=&\mathbf a+t\left(\begin{array}{c}0\\1\end{array}\right) &&\parallel \text{ zur $y$-Achse} \end{array} \end{gathered} \tag{8.2}\]
8.3 Funktionen mit zwei Variablen
Unter einer Funktion \(f\) mit zwei Variablen versteht man eine Zuordnungsvorschrift \(f:M\to\mathbb R\), die jedem Vektor \(\mathbf x=\left(\begin{array}{c}x\\y\end{array}\right)\) einer Teilmenge \(M\subseteq\mathbb R^2\) eine Zahl \(z=f(x,y)\) zuordnet. Die Menge \(M\) nennt man den Definitionsbereich der Funktion \(f\).
Zur Schreibweise: wir schreiben \(f(x,y)\), oder auch \(f(\mathbf x)\), und meinen dabei stets dasselbe.
In den meisten wirtschaftlichen Anwendungen benötigt man als Definitionsbereich der auftretenden Funktionen nur den nichtnegativen Quadranten \[ \begin{gathered} \mathbb R_+^2:=\{(x,y): x\geq 0,\,y\geq 0\}. \end{gathered} \] Man kann Funktionen mit zwei Variablen durch Diagramme veranschaulichen. Die beiden wichtigsten Typen von Diagrammen sind:
- perspektivische Bilder des Funktionsgraphen: \[ \begin{gathered} G_f=\{(x,y,z): z=f(x,y),\;\mathbf x\in M\}, \end{gathered} \]
- und Bilder von Niveaulinien: \[ \begin{gathered} L_c=\{(x,y): f(x,y)=c,\,\mathbf x\in M, c\in \mathbb R\}. \end{gathered} \]
Perspektivische Bilder des Funktionsgraphen zu erzeugen ist ein recht aufwendiger Prozess, den wir am besten mit Hilfe geeigneter Graphik-Software durchführen lassen (Beispiele folgen!).
Niveaulinien bedürfen einer Erläuterung: Der Graph \(G_f\) ist im allgemeinen eine mehr oder weniger kompliziert gewölbte Fläche im \(\mathbb R^3\). Nehmen wir nun ein virtuelles Messer2 und schneiden horizontal, also parallel zu \((x,y)-\)Ebene in Höhe \(c\) durch das Funktionsgebirge. Dann erhalten wir Schnittflächen, deren Rand gerade die Niveaulinien auf Höhe \(c\) sind. Sie sind nichts anderes als Höhenschichtlinien, die Sie von Wanderkarten her kennen. Die geübte Wanderin weiß diese Karten auch richtig zu lesen: dort, wo die Höhenschichtlinien dicht beieinander verlaufen, geht es durch steiles Gelände, dort, wo sie weiter auseinander liegen, geht es gemütlich dahin. Genauso interpretieren wir Niveaulinien.
Die nun folgenden Beispiele dienen zwei Zielen: einerseits wollen wir uns eine kleine Liste wichtiger Funktionen zusammenstellen, andererseits sollen die eben erörterten Konzepte der perspektivische Darstellung und der Niveaulinien illustriert werden.
8.3.1 Lineare Funktionen
Definition 8.4 Unter einer linearen Funktion mit zwei Variablen versteht man eine Funktion mit dem Funktionsterm \[ \begin{gathered} z=f(x,y)=b_1x+b_2y+c. \end{gathered} \] Ist \(c=0\), dann nennt man \(f(x,y)\) eine homogene lineare Funktion.
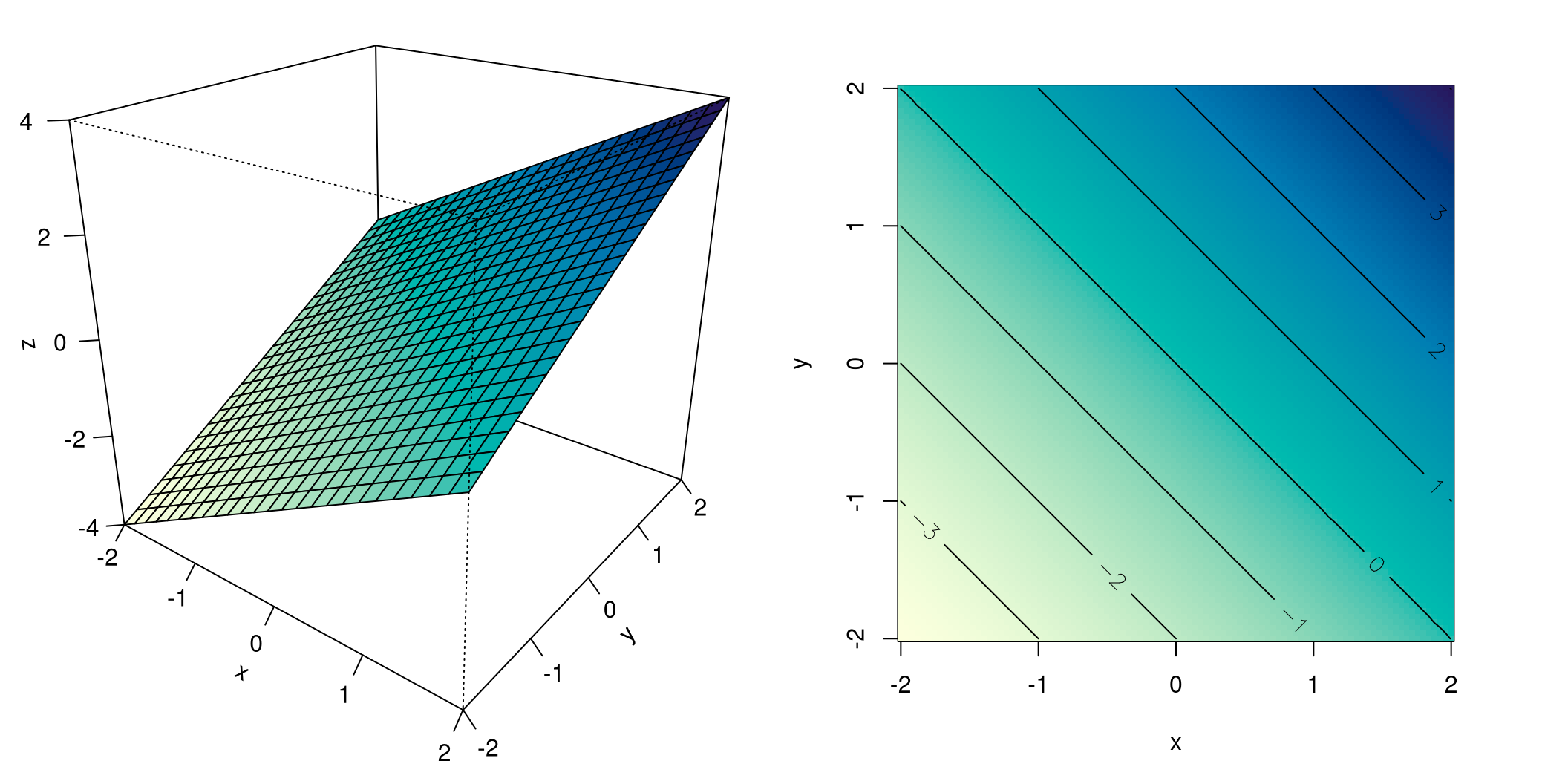
Abbildung 8.4 zeigt die lineare Funktion \(f(x,y)=x+y\), links sehen Sie eine perspektivische Darstellung, das Bild einer mehr oder weniger schief im Raum hängenden Ebene, die den Nullpunkt \(\boldsymbol{0}\) enthält.
Rechts sehen Sie die Niveaulinien dieser Funktion: sie sind parallele und in gleichem Abstand verlaufende Geraden. Jede Gerade ist dabei mit dem Wert des zugehörigen Niveaus beschriftet.
Sowohl die perspektivische Darstellung als auch die Niveaulinien sind außerdem mit dem gleichen Farbverlauf hinterlegt, der ähnlich wie bei Wanderkarten nochmals die Niveaus der Funktionswerte kodiert: von hellem Gelb bis zu dunklem Blau für den Verlauf von niedrigen zu hohen Funktionswerten.
Der Funktionsterm einer homogenen linearen Funktion lässt sich als Matrixprodukt schreiben: \[ \begin{gathered} f(x,y)=b_1x+b_2y={\mathbf b}^\top \mathbf x,\quad \text{wobei }\mathbf x=\left(\begin{array}{c}x\\y\end{array}\right), \mathbf b=\left(\begin{array}{c}b_1\\b_2\end{array}\right). \end{gathered} \]
8.3.2 Quadratische Funktionen
Definition 8.5 Unter einer quadratischen Funktion mit zwei Variablen versteht man eine Funktion mit dem Funktionsterm \[ \begin{gathered} z=f(x,y)=a_{11}x^2+2a_{12}xy+a_{22}y^2+ b_1x+b_2y+c. \end{gathered} \] Sind \(b_1=b_2=c=0\), dann nennen wir \[ \begin{gathered} f(x,y)=a_{11}x^2+2a_{12}xy+a_{22}y^2 \end{gathered} \] eine homogene quadratische Funktion.
Der maximale Definitionsbereich eines quadratischen Funktionsterms ist \(\mathbb R^2\).
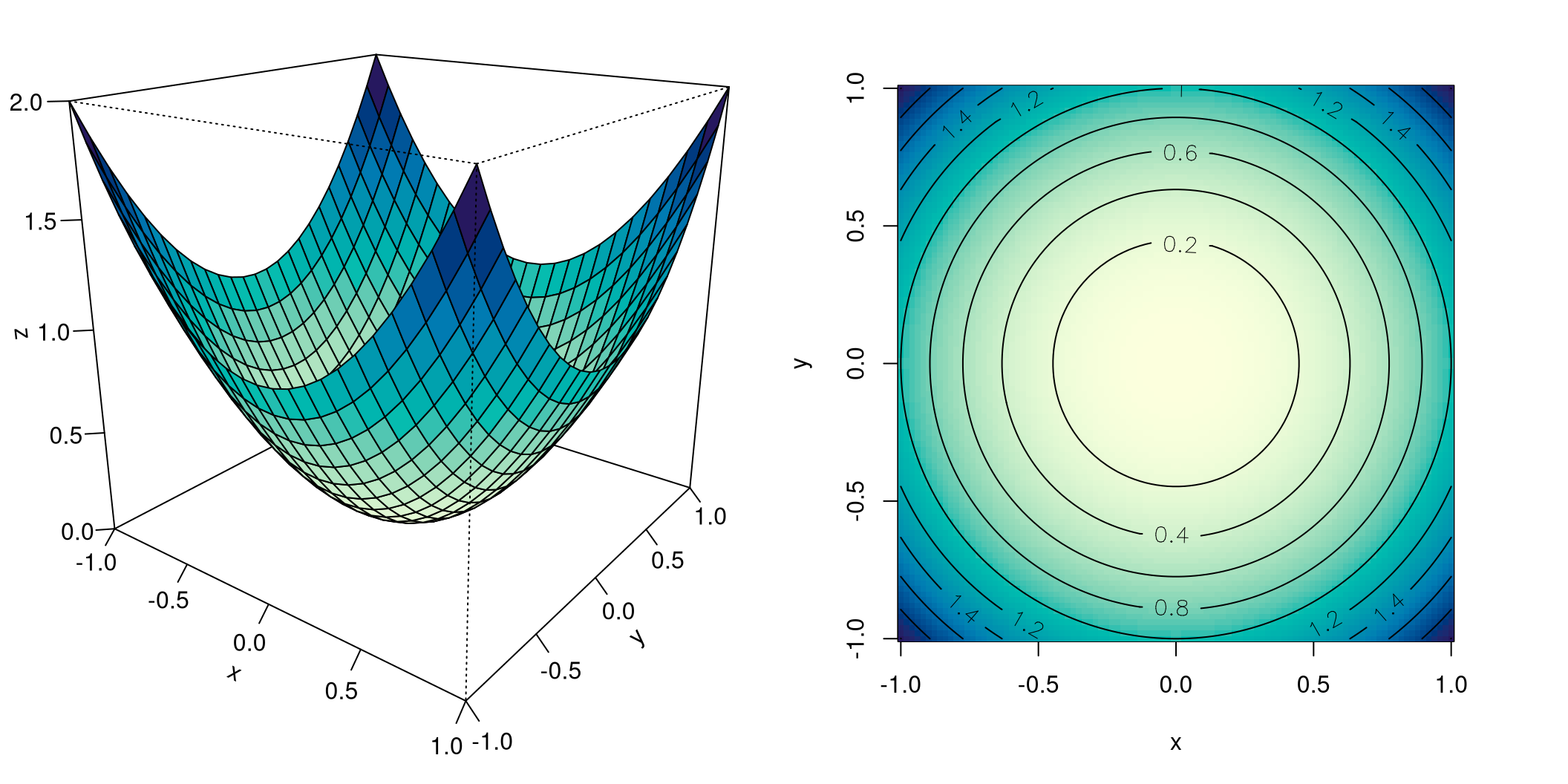
Abbildung 8.5 zeigt die homogene quadratische Funktion \(f(x,y)=x^2+y^2\). Die perspektivische Darstellung zeigt eine konvexe Fläche. Interessant sind die Niveaulinien: das sind konzentrische Kreise, deren Abstände immer kleiner werden. Wir sehen auch warum: der Funktionsgraph verläuft immer steiler, je mehr wir uns von seinem Minimalpunkt entfernen, in welche Richtung auch immer.
Nun nehmen wir im eben gezeigten Beispiel eine minimale Änderung vor, nur ein Vorzeichen soll anders sein. Jetzt sehen wir uns die quadratische Funktion \(f(x,y)=x^2-y^2\) an:
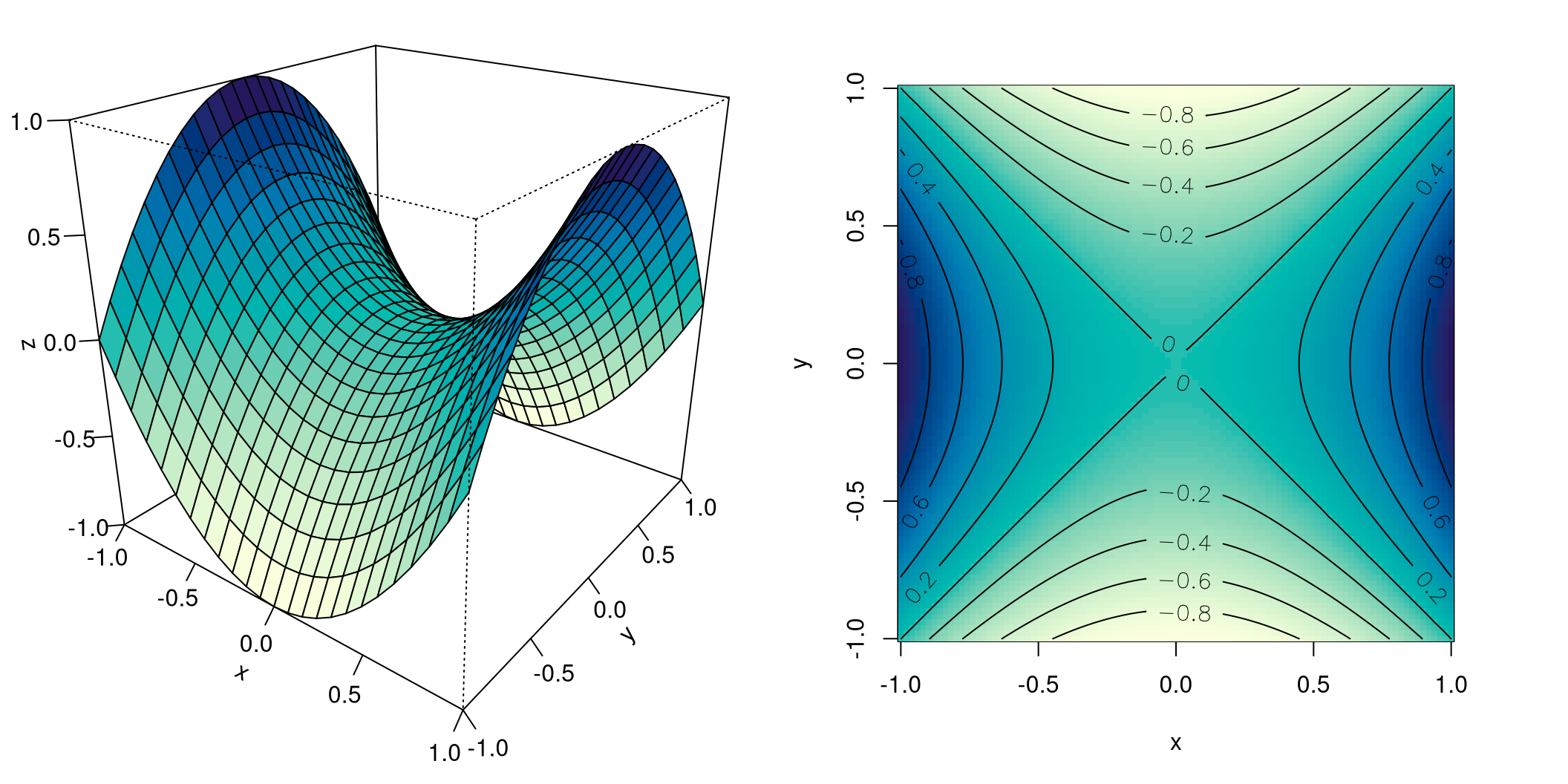
Es ist ein ganz anderes Bild, das sich uns bietet! Die perspektivische Darstellung zeigt eine Sattelfläche, die Niveaulinien sind nun konzentrische Hyperbeln. Auch an ihnen ist zu sehen, dass sie immer näher zusammenrücken, und zwar in vier Richtungen. Das sind eben jene Richtungen, in denen es auf der Sattelfläche steil bergauf bzw. steil bergab geht.
Homogene quadratische Funktionen werden in unserer Arbeit noch eine wichtige Rolle spielen, daher überlegen wir uns ebenfalls, wie wir sie als Matrixprodukte darstellen können. Das ist tatsächlich einfach, freilich sind aber wegen der quadratischen Terme zwei Matrixmultiplikationen notwendig: \[ \begin{aligned} f(x,y)&=a_{11}x^2+2a_{12}xy+a_{22}y^2\\[5pt] &=(x,y)\left(\begin{array}{cc}a_{11} & \cellcolor{lgray}a_{12}\\ \cellcolor{lgray}a_{12} & a_{22}\end{array}\right) \left(\begin{array}{c}x\\y\end{array}\right)={\mathbf x}^\top \mathbf A\mathbf x. \end{aligned} \] Man nennt \(\mathbf A\) die erzeugende Matrix und wir nehmen an, dass diese Matrix symmetrisch ist, also \({\mathbf A}^\top =\mathbf A\). Diese Annahme ist nicht notwendig, aber sinnvoll im Hinblick auf die Anwendungen, die wir vorhaben.
Wir halten fest, dass es niemals notwendig ist, die Matrixmultiplikationen auszuführen. Bei gegebener Matrix \(\mathbf A\) können wir die quadratische Funktion unmittelbar ablesen. Die Zahlen in der Hauptdiagonalen sind die Koeffizienten von \(x^2\) und \(y^2\), die Summe der Nebendiagonalkomponenten ist der Koeffizient von \(xy\).
Musteraufgabe 8.6 Welche homogene quadratische Funktion wird durch die Matrix \[ \begin{gathered} \mathbf A=\left(\begin{array}{rr}-2 & 5 \\5 & 8\end{array}\right) \end{gathered} \] erzeugt?
Lösung: \(f(x,y)=-2x^2+10xy+8y^2\). □
Auch der umgekehrte Weg ist sehr einfach, nämlich bei gegebenem Funktionsterm die erzeugende Matrix zu finden.
Wir führen einfach einen Koeffizientenvergleich durch: Der Koeffizient von \(x^2\) ist \(a_{11}\), jener von \(y^2\) ist \(a_{22}\), schließlich ist \(2a_{12}\) der Koeffizient von \(xy\).
Musteraufgabe 8.7 Man bestimme die Matrixdarstellung der homogenen quadratischen Funktionen
-
\(f(x,y)=2x^2-4xy+y^2\),
-
\(f(x,y)=x^2-3y^2\),
- \(f(x,y)=-6xy\).
Lösung: Wir lösen die Aufgabe durch Koeffizientenvergleich.
(a) \(2x^2\implies a_{11}=2\), \(y^2\implies a_{22}=1\), \(-4xy \implies a_{12}=-2\), daher ist die erzeugende Matrix: \[ \begin{gathered} \mathbf A=\left(\begin{array}{rr}2 & -2\\-2 & 1\end{array}\right). \end{gathered} \]
Auf die gleiche Weise finden wir:
(b) \(\mathbf A=\left(\begin{array}{rr}1 & 0\\0 & -3\end{array}\right)\), (c) \(\mathbf A=\left(\begin{array}{rr}0 & -3\\-3 & 0\end{array}\right)\). □
Satz 8.8 Die allgemeine quadratische Funktion besitzt die Matrixform: \[ \begin{gathered} f(\mathbf x)={\mathbf x}^\top \mathbf A \mathbf x+{\mathbf b}^\top \mathbf x+c,\qquad\text{wobei }{\mathbf A}^\top =\mathbf A\text{ und }\mathbf x=\left(\begin{array}{c}x\\y\end{array}\right). \end{gathered} \]
8.3.3 Cobb-Douglas-Funktionen
In nationalökonomischen Anwendungen spielen sogenannte Cobb-Douglas-Funktionen eine wichtige Rolle.
Definition 8.9 Unter einer Cobb-Douglas-Funktion mit zwei Variablen versteht man eine Funktion mit dem Funktionsterm \[ \begin{gathered} z=f(x,y)=Cx^{\alpha}y^{\beta}, \end{gathered} \] wobei \(\alpha\geq 0\) und \(\beta\geq 0\).
Der maximale Definitionsbereich einer Cobb-Douglas-Funktion ist für gewöhnlich \(\mathbb R_+^2\), der nichtnegative Quadrant.
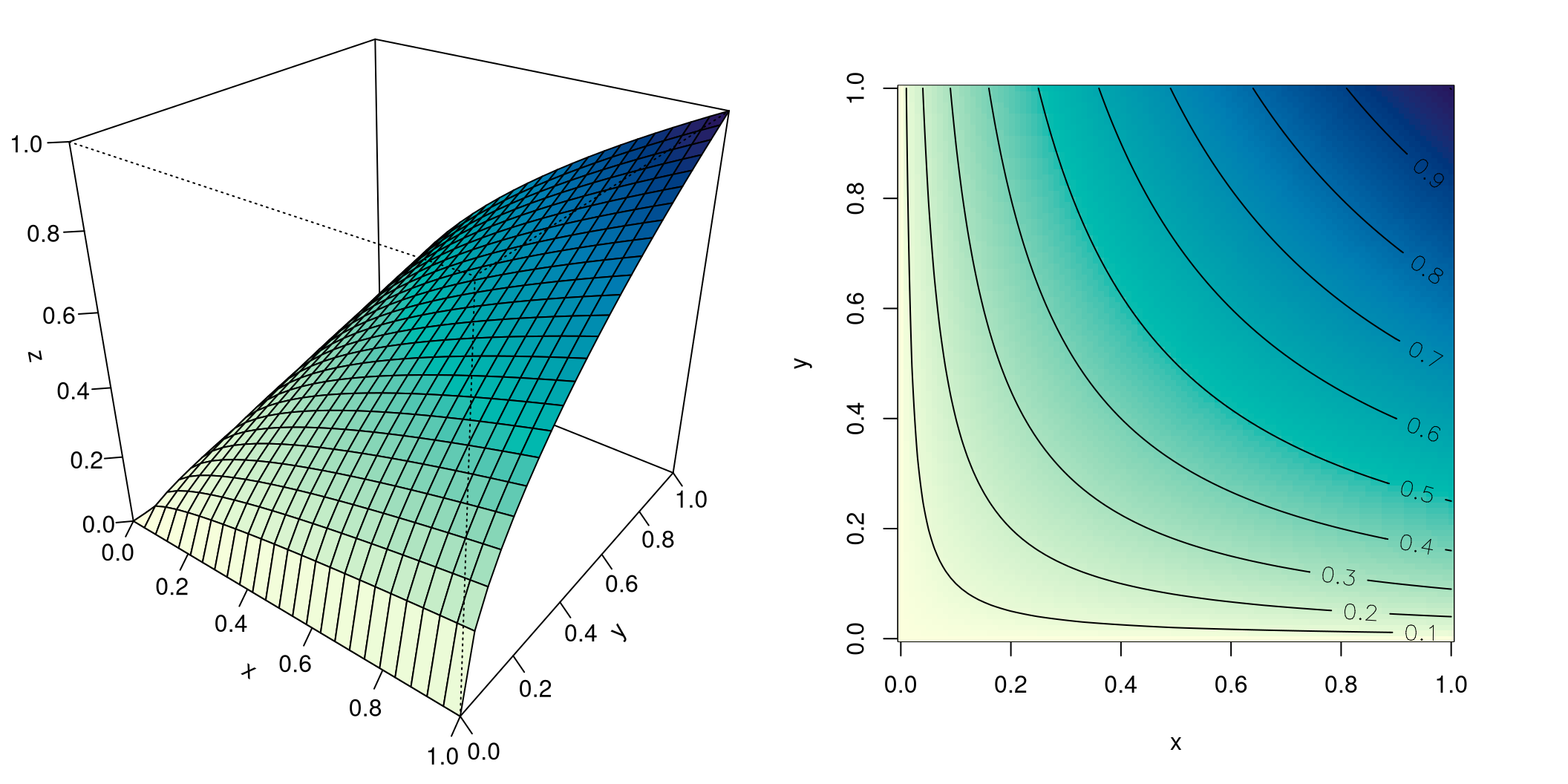
Cobb-Douglas-Funktionen werden gerne als Produktionsfunktionen verwendet. In diesem Fall beschreiben \(x\) und \(y\) den Faktoreinsatz, etwa Mengen an Rohstoffen, Energie, usw. Der Funktionswert \(f(x,y)\) ist der Output bei gegebenem Faktoreinsatz \(x\) und \(y\). In einem makroökonomischen Kontext könnte \(x\) die Höhe des gesamtwirtschaftlichen Kapitalstocks sein, \(y\) die gesamtwirtschaftliche Lohnsumme, \(f(x,y)\) das BIP. Die Niveaulinien der Cobb-Douglas-Funktion sind Kurven gleichen Outputs, sie heißen Isoquanten.
8.3.4 Homogene Funktionen
Während wir für lineare und quadratische Funktionen homogene Varianten angegeben hatten, geschah das nicht für Cobb-Douglas-Funktionen. Der Grund ist ein einfacher: Cobb-Douglas-Funktionen sind schon von sich aus homogen.
Wir klären nun den Begriff der Homogenität:
Definition 8.10 Eine Funktion \(f(x,y)\) heißt homogen vom Grad \(k\), wenn für alle \(t>0\): \[ \begin{gathered} f(tx,ty)=t^kf(x,y), \qquad k\in \mathbb R. \end{gathered} \tag{8.3}\]
Die Eigenschaft der Homogenität ist vor allem (aber nicht nur) dann von Interesse, wenn \(f(x,y)\) eine Produktionsfunktion ist. Nun sind \(x\) und \(y\) die eingesetzten Mengen von zwei Produktionsfaktoren. Werden diese Mengen verdoppelt, also \(t=2\), dann ändert sich der Output um den Faktor \(2^k\). Ist \(k=1\), heißt das, dass eine Verdopplung des Inputs zu einer Verdopplung des Outputs führt, man sagt auch, die Produktionsfunktion \(f(x,y)\) hat konstante Skalenerträge.
Ist \(k<1\), dann besitzt \(f(x,y)\) abnehmende Skalenerträge, wenn \(k>1\), dann sind die Skalenerträge zunehmend.
Eine Cobb-Douglas-Funktion ist homogen vom Grad \(\alpha+\beta\), denn: \[ \begin{gathered} f(tx,ty)=C(tx)^\alpha(ty)^\beta=Ct^\alpha x^\alpha t^\beta y^\beta= Ct^{\alpha+\beta}x^\alpha y^\beta=t^{\alpha+\beta}f(x,y) \end{gathered} \]
8.4 Die erste Ableitung
8.4.1 Die Richtungsableitung
In Kapitel 3 definierten wir die erste Ableitung einer Funktion \(f(x)\) in einem Punkt \(x_0\) als die Änderungsrate der Funktion in diesem Punkt. Nun ist aber unser Punkt \(\mathbf x=\mathbf a\) ein Element des \(\mathbb R^2\), und in diesem Punkt wird das Änderungsverhalten der Funktion \(f(\mathbf a)\) davon abhängen, in welche Richtung \(\mathbf v\) wir von \(\mathbf a\) aus schauen.
Um konkret zu werden was die Richtung betrifft, stellen wir uns eine gleichförmige Bewegung in der Ebene \(\mathbb R^2\) vor. Sie verlaufe durch den Punkt \(\mathbf a\) und folge dem Verschiebungsvektor \(\mathbf v\ne \boldsymbol{0}\). Mit anderen Worten: \[ \begin{gathered} \mathbf x=\mathbf a+t\mathbf v\Leftrightarrow \left\{\begin{array}{ccc} x&=&a_1+tv_1\\ y&=&a_2+tv_2 \end{array} \right.,\qquad t\in\mathbb R \end{gathered} \] Für jeden Parameterwert \(t\in\mathbb R\) berechnen wir \(\mathbf x=\mathbf a+t\mathbf v\) und den dazugehörigen Funktionswert \(f(\mathbf x)\). Dadurch erhalten wir eine Funktion \[ \begin{gathered} c(t)=f(\mathbf a+t\mathbf v)=f(a_1+tv_1,a_2+tv_2). \end{gathered} \] Diese Funktion beschreibt die Funktionswerte von \(f\) entlang der gleichförmigen Bewegung \(\mathbf x=\mathbf a+t\mathbf v\). Und, was wesentlich ist: \(c(t)\) ist eine Funktion in nur mehr einer Variablen \(t\)!
Wir interessieren uns nun für die Änderungsraten der Funktion \(c(t)\). Zu diesem Zweck berechnen wir die Ableitung \(c'(t)\).
Bevor wir dem Kind einen Namen geben, betrachten wir ein konkretes Beispiel.
Es sei \(f(x,y)=3-x^2-y^2\), und \(\mathbf x\) folge der gleichförmigen Bewegung: \[ \begin{gathered} \mathbf x=\left(\begin{array}{c}-1\\-2\end{array}\right)+t\left( \begin{array}{r}1\\1\end{array}\right) \quad\Leftrightarrow\quad \left\{\begin{array}{ccl} x&=&-1 + t\\ y&=&-2 + t \end{array} \right. \end{gathered} \] Wir setzen nun \(x\) und \(y\) in \(f(x,y)\) ein und erhalten so: \[ \begin{aligned} c(t)&=3-(-1 + t)^2-(-2 + t)^2\\ &=-2+6t-2t^2, \end{aligned} \] mit erster Ableitung: \[ \begin{gathered} c'(t)=6-4t. \end{gathered} \]
Die Funktionen aus Beispiel 8.11 sind in Abbildung 8.8 dargestellt.

Das, was wir soeben getan haben, können wir uns am besten so veranschaulichen: mit einem virtuellen Messer führen wir einen zur \((x,y)-\)Ebene senkrechten Schnitt durch das Funktionsgebirge. Dabei soll
- der Schnitt durch den Punkt \(\mathbf a\) verlaufen, und
- die Richtung \(\mathbf v\) haben.
Es entsteht eine Schnittfläche mit einem Rand, das ist gerade die Funktion \(c(t)\). Wenn \(c(t)\) differenzierbar ist, können wir ihre Ableitung \(c'(t)\) bilden. Ihr Wert an der Stelle \(t=0\) heißt Richtungsableitung im Punkt \(\mathbf x=\mathbf a\).
Definition 8.12 Es sei \(f(x,y)\) eine Funktion in zwei Variablen und \(\mathbf x=\mathbf a+t\mathbf v\). Besitzt die Funktion \[ \begin{gathered} c(t)=f(a_1+tv_1,a_2+tv_2) \end{gathered} \] eine erste Ableitung in \(t=0\), so nennt man \(c'(0)\) die Richtungsableitung von \(f(x,y)\) im Punkt \(\mathbf x=\mathbf a\). Sie gibt uns die Änderungsrate von \(f(x,y)\) im Punkt \(\mathbf a\) in Richtung \(\mathbf v\) an.
Musteraufgabe 8.13 Bestimme die Richtungsableitung von \(f(x,y)=xe^y\) im Punkt \(\mathbf a=\left(\begin{array}{r}-1\\1\end{array}\right)\) in Richtung \(\mathbf v=\left(\begin{array}{r}2\\-3\end{array}\right)\).
Lösung: Aus der gleichförmigen Bewegung \(\mathbf x=\mathbf a+t\mathbf v\) erhalten wir: \[ \begin{gathered} x=-1+2t,\quad y=1-3t. \end{gathered} \] Einsetzen in \(f(x,y)\) ergibt: \[ \begin{aligned} c(t)&=(-1+2t)e^{1-3t},\\[4pt] c'(t)&=2e^{1-3t}-3(-1+2t)e^{1-3t}=(5-6t)e^{1-3t},\\[4pt] c'(0)&=5e\simeq 13.59\,. \end{aligned} \] □
8.4.2 Partielle Ableitungen erster Ordnung
Wenn wir in der Richtungsableitung den Vektor \(\mathbf v\) parallel zu der \(x\)- oder \(y\)-Achse ausrichten, dann erhalten wir die partiellen Ableitungen erster Ordnung von \(f(x,y)\).
Definition 8.14 (Partielle Ableitung) Unter einer partiellen Ableitung einer Funktion \(f(x,y)\) mit zwei Variablen versteht man die Ableitung der Funktion \(f\) nach einer der beiden Variablen \(x\) oder \(y\), wobei die andere Variable als Konstante behandelt wird.
Wenn wir parallel zur \(x\)-Achse differenzieren, dann ist \(\mathbf v=\left(\begin{array}{c}1\\0\end{array}\right)\). Wir nennen dies die erste partielle Ableitung nach \(x\) und schreiben dafür \[ \begin{gathered} f_1'(x,y)\quad\text{oder}\quad \frac{\partial f}{\partial x}. \end{gathered} \] Rechnerisch erhalten wir diese Ableitung dadurch, dass wir \(y\) wie eine Konstante behandeln. Geometrisch: wir schneiden parallel zur \(x\)-Achse vertikal und differenzieren den so entstehenden Rand, siehe Abbildung 8.9 links.
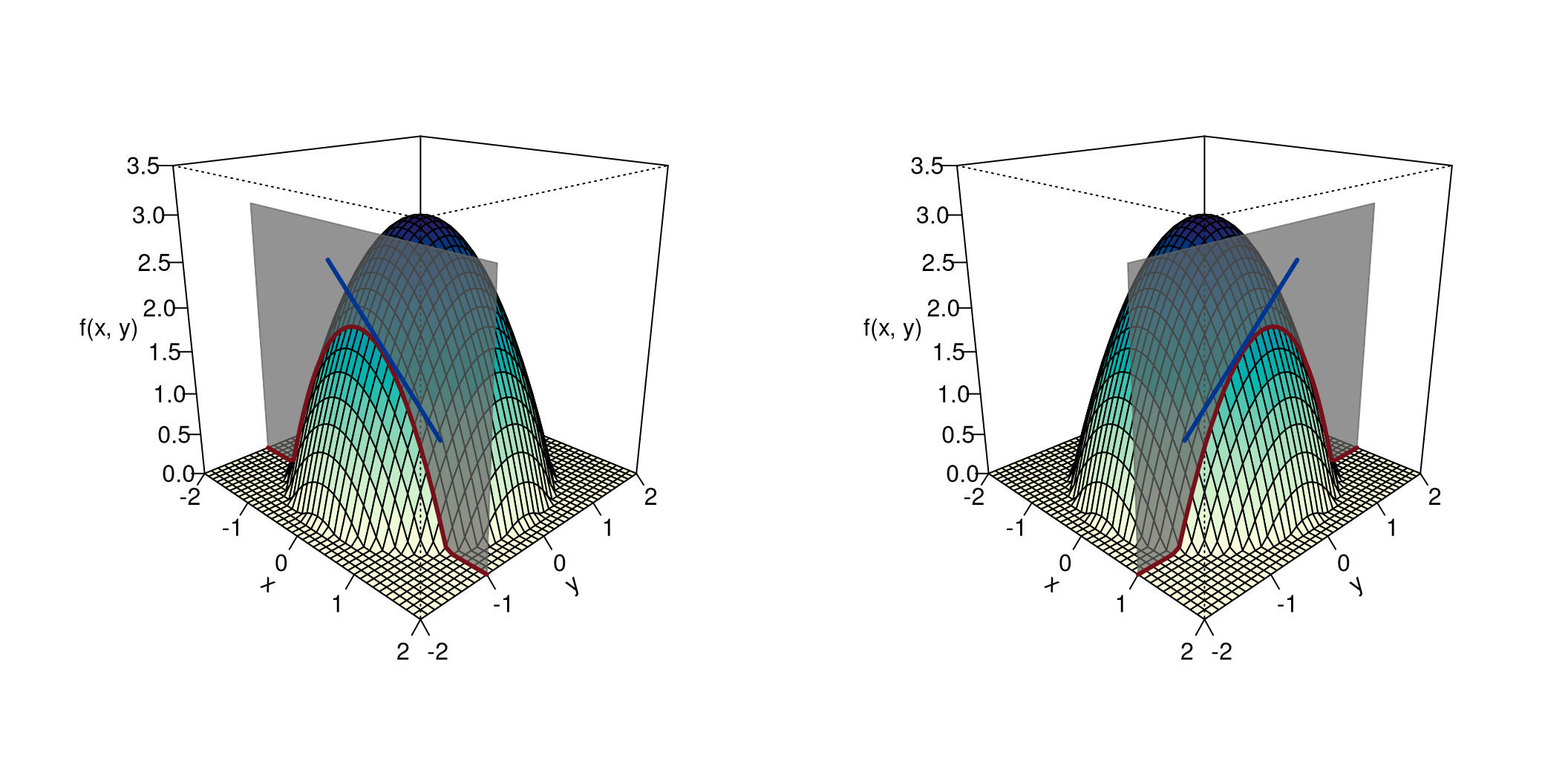
Differenzieren wir hingegen parallel zur \(y\)-Achse, dann ist \(\mathbf v=\left(\begin{array}{c}0\\1\end{array}\right)\). Wir nennen dies die erste partielle Ableitung nach \(y\) und schreiben dafür \[ \begin{gathered} f_2'(x,y)\quad\text{oder}\quad \frac{\partial f}{\partial y}. \end{gathered} \] Nun wird \(x\) wie eine Konstante behandelt, d.h. wir schneiden parallel zur \(y\)-Achse vertikal und differenzieren den so entstehenden Rand, siehe Abbildung 8.9 rechts.
Definition 8.15 Den Spaltenvektor der ersten partiellen Ableitungen \[ \begin{gathered} \boldsymbol{f}'(\mathbf x)=\frac{\partial f}{\partial \mathbf x}=\left( \begin{array}{c} \frac{\partial f}{\partial x}\\[4pt] \frac{\partial f}{\partial y} \end{array}\right) \end{gathered} \] nennen wir die erste Ableitung oder den Gradienten von \(f\).
Musteraufgabe 8.16 Man finde die ersten partiellen Ableitungen der Funktion \(f(x,y)=3x^2+e^{2y}\) an der Stelle \(x=-1\) und \(y=0\).
Lösung: Wir differenzieren zuerst partiell nach \(x\). Das bedeutet, dass \(y\) wie eine Konstante behandelt werden muss. Als solche kann sie auftreten:
- Als konstanter Faktor in einem Produkt, dann bleibt dieser unverändert erhalten;
- Oder als additive Konstante. Diese wird beim Differenzieren Null.
Wenn \(y\) konstant ist, dann ebenso \(e^{2y}\), das als additive Konstante in \(f(x,y)\) auftritt. Die Ableitung dieses Terms nach \(x\) ist deshalb Null. Daher \[ \begin{gathered} f_1'(x,y)=\frac{\partial f}{\partial x}=6x+0=6x,\\[4pt] f_1'(-1,0)=-6. \end{gathered} \] Wenn wir hingegen partiell nach \(y\) differenzieren, dann ist \(x\) wie eine Konstante zu behandeln. Nun ist die Ableitung von \(e^{2y}\) nach \(y\) gegeben durch \(2e^{2y}\), der Term \(3x^2\) ist eine additive Konstante bezüglich \(y\). Daher: \[ \begin{gathered} f_2'(x,y)=\frac{\partial f}{\partial y} =0+2e^{2y}=2e^{2y},\\[4pt] f_2'(-1,0)=2. \end{gathered} \] □
Musteraufgabe 8.17 Man finde die ersten partiellen Ableitungen der Funktion \(f(x,y)=3x^2e^{2y}\) an der Stelle \(x=-1\) und \(y=0\).
Lösung: Wenn wir partiell nach \(x\) differenzieren, ist \(e^{2y}\) ein konstanter Faktor und bleibt als solcher erhalten: \[ \begin{aligned} f_1'(x,y)&=6xe^{2y},\qquad f_1'(-1,0)=-6. \end{aligned} \] Differenzieren wir hingegen nach \(y\), dann ist \(3x^2\) ein konstanter Faktor: \[ \begin{gathered} f_2'(x,y)=3x^2\cdot 2e^{2y}=6x^2e^{2y},\qquad f_2'(-1,0)=6. \end{gathered} \] □
Musteraufgabe 8.18 Man finde die ersten partiellen Ableitungen der Funktion \(f(x,y)=\ln(2x-5y)\) an der Stelle \(x=3\) und \(y=1\).
Lösung: Hier brauchen wir die Kettenregel für den Logarithmus (siehe Satz 3.32). Beim Differenzieren nach \(x\) ist \(-5y\) eine additive Konstante der inneren Funktion des Logarithmus: \[ \begin{aligned} f_1'(x,y)&=\frac{2}{2x-5y}\qquad \text{(2 ist die innere Ableitung: $(2x)'=2$)},\\[4pt] f_1'(3,1)&=2. \end{aligned} \] Analog: \[ \begin{aligned} f_2'(x,y)&=-\frac{5}{2x-5y}\qquad \text{($-5$ ist die innere Ableitung: $(-5y)'=-5$)},\\[4pt] f_2'(3,1)&=-5. \end{aligned} \] □
Musteraufgabe 8.19 Man finde die ersten partiellen Ableitungen der Funktion \(f(x,y)=5x^2e^{x-y^2}\) an der Stelle \(x=1\) und \(y=0\).
Lösung: Beim Bilden der ersten Ableitung nach \(x\) müssen wir die Produktregel anwenden: \[ \begin{gathered} f_1'(x,y)=10xe^{x-y^2}+5x^2e^{x-y^2}=5x(2+x)e^{x-y^2},\\[5pt] f_1'(1,0)=15e\simeq 40.7742\,. \end{gathered} \] Nun die Ableitung nach \(y\) (hier brauchen wir die Kettenregel): \[ \begin{gathered} f_2'(x,y)=5x^2(-2y)e^{x-y^2}=-10x^2ye^{x-y^2},\\[5pt] f_2'(1,0)=0. \end{gathered} \] □
8.4.3 Ableitung linearer und quadratischer Funktionen
Eine lineare Funktion in einer Variablen, nämlich \(y=bx+c\) besitzt die erste Ableitung \(y'=b\). Völlig analog gilt für lineare Funktionen in zwei Variablen: \[ \begin{aligned} f(\mathbf x)&={\mathbf b}^\top \mathbf x+c=b_1x+b_2y+c,\\[5pt] \left. \begin{array}{rcl}f_1'(\mathbf x)&=&b_1\\[5pt] f_2'(\mathbf x)&=&b_2\end{array} \right\}&\implies\boldsymbol{f}'(\mathbf x)=\mathbf b. \end{aligned} \] Eine allgemeine quadratische Funktion in einer Variablen hat die Gestalt \(y=ax^2+bx+c\) mit erster Ableitung \(y'=2ax+b\). Genauso sieht das aus für quadratische Funktionen in zwei Variablen!
In Satz 8.8 haben wir die Matrixform einer allgemeinen quadratischen Funktionen angegeben: \[ \begin{gathered} f(\mathbf x)={\mathbf x}^\top \mathbf A \mathbf x+{\mathbf b}^\top \mathbf x+c. \end{gathered} \] Was ist ihre erste Ableitung? Wir beginnen mit dem homogenen Anteil: \[ \begin{aligned} & {\mathbf x}^\top \mathbf A \mathbf x =a_{11}x^2+2a_{12}xy+a_{22}y^2\\[5pt] &\left.\begin{array}{rcl} \frac{\partial}{\partial x}{\mathbf x}^\top \mathbf A \mathbf x &\!=\!&2a_{11}x+2a_{12}y\\[5pt] \frac{\partial}{\partial y}{\mathbf x}^\top \mathbf A \mathbf x &\!=\!&2a_{12}x+2a_{22}y \end{array}\right\}\!\implies\\ & \frac{\partial}{\partial\mathbf x} {\mathbf x}^\top \mathbf A \mathbf x\!=\! 2\left(\!\begin{array}{cc}a_{11} & a_{12}\\a_{12} & a_{22}\end{array} \!\right)\left(\begin{array}{c}x\\y\end{array}\right)\!=\! 2\mathbf A\mathbf x \end{aligned} \] Nun fügen wir das alles zusammen:
Satz 8.20 (Ableitung einer quadratischen Funktion) Es sei \[ \begin{gathered} f(\mathbf x)={\mathbf x}^\top \mathbf A \mathbf x+{\mathbf b}^\top \mathbf x+c \end{gathered} \] eine allgemeine quadratische Funktion. Dann ist ihre erste Ableitung: \[ \begin{gathered} \boldsymbol{f}'(\mathbf x)=2\mathbf A\mathbf x+\mathbf b. \end{gathered} \]
8.4.4 Partielle Änderungsraten und Elastizitäten
Die partiellen Ableitungen \(f_1'(x,y)\) und \(f_2'(x,y)\) messen die Änderungsrate von \(f(x,y)\) in Richtung der \(x-\)Achse bzw. der \(y-\)Achse, wenn die jeweils andere Variable konstant gehalten wird. Analog zum Falle einer Variablen, der in Kapitel 3 behandelt wurde, können wir für Funktionen in zwei Variablen partielle Elastizitäten definieren als Reaktionsmaße. Sie ergeben sich als partielle Ableitung des Logarithmus (relative Änderungsrate) multipliziert mit \(x\) bzw. \(y\):
Definition 8.21 Es sei \(f(x,y)>0\) eine nach \(x\) und \(y\) partiell differenzierbare Funktion, dann nennt man \[ \begin{aligned} \epsilon_1(x,y)&=\frac{f_1'(x,y)}{f(x,y)}\cdot x=\frac{\partial\ln f(x,y)}{\partial x}\cdot x,\\[5pt] \epsilon_2(x,y)&=\frac{f_2'(x,y)}{f(x,y)}\cdot y=\frac{\partial\ln f(x,y)}{\partial y}\cdot y, \end{aligned} \tag{8.4}\] partielle Elastizitäten bezüglich \(x\) bzw. \(y\).
Die Elastizität \(\epsilon_1(x,y)\) sagt uns, um wieviel Prozent sich \(f(x,y)\) bei einer kleinen prozentuellen Änderung von \(x\) ändert, wenn \(y\) konstant gehalten wird. Analog interpretieren wir \(\epsilon_2(x,y)\).
Musteraufgabe 8.22 Es sei \(f(x,y)=100x^{0.3}y^{0.7}\) eine Produktionsfunktion, \(x\) und \(y\) sind die eingesetzten Mengen zweier Produktionsfaktoren, \(f(x,y)\) der erzielte Output. Zu berechnen sind die partiellen Produktionselastizitäten, d.h. die Elastizitäten von \(f\) bezüglich \(x\) und \(y\).
Lösung: Es handelt sich hier um eine linear homogene Cobb-Doubglas-Funktion, für die die partiellen Produktionselastizitäten eine besonders einfache Form haben. Wir brauchen die logarithmischen Ableitungen, daher bilden wir zuerst: \[ \begin{gathered} \ln f(x,y)=\ln\left(100x^{0.3}y^{0.7}\right)=\ln 100+0.3\ln x+0.7\ln y. \end{gathered} \] Die logaritmischen Ableitungen sind: \[ \begin{gathered} \frac{\partial \ln f(x,y)}{\partial x}=\frac{0.3}{x},\qquad \frac{\partial \ln f(x,y)}{\partial y}=\frac{0.7}{y}. \end{gathered} \] Aus (8.4) folgt nun: \[ \begin{gathered} \epsilon_1(x,y)=\frac{0.3}{x}\cdot x=0.3,\qquad \epsilon_2(x,y)=\frac{0.7}{y}\cdot y=0.7\,. \end{gathered} \] Wir sehen, dass diese Elastizitäten konstant und unabhängig vom Faktoreinsatz sind. Überdies stimmen sie mit den Exponenten in \(f(x,y)\) überein.
Ganz allgemein gilt für eine Cobb-Douglas-Funktion \(f(x,y)=Cx^\alpha y^\beta\): \[ \begin{gathered} \epsilon_1(x,y)=\alpha,\qquad \epsilon_2(x,y)=\beta. \end{gathered} \] Dies ist eine wichtige Verallgemeinerung von Satz 3.54.
Bemerkung 8.23 (Kreuzpreiselastizität) Es kommt vor, dass die nachgefragte Menge \(q\) eines Gutes \(Q\) nicht nur von dessen Preis \(p_1\) abhängt, sondern auch vom Preis \(p_2\) eines konkurrierenden Gutes \(R\). Die Nachfragefunktion nach \(Q\) hat dann die Form einer Funktion in zwei Variablen \(q:=q(p_1,p_2)\).
Als Kreuzpreiselastizität bezeichnet man \(\epsilon_2(p_1,p_2)\). Sie misst, wie stark die Nachfrage nach \(Q\) reagiert, wenn sich der Preis des Konkurrenzprodukts \(R\) ändert. Wenn \(\epsilon_2(p_1,p_2)>0\), so bedeutet das: wird das Konkurrenzprodukt \(R\) teurer, dann weichen Konsumenten aus und konsumieren mehr von \(Q\). Man sagt auch, die beiden Güter sind substitutiv oder supplementär, wie z. B. Energie aus Wasserkraft und Atomstrom. Umgekehrt, wenn \(\epsilon_2(p_1,p_2)<0\), so führt ein steigender Preis von \(R\) zu einer geringeren Nachfrage von beiden Gütern \(Q\) und \(R\). Die beiden Güter sind komplementär, wie z.B. Kaffeemaschinen und Kaffeekapseln.
Musteraufgabe 8.24 Die nachgefragte Menge \(q\) eines Gutes \(Q\) hängt nicht nur von seinem Preis \(p_1\) ab, sondern auch vom Preis \(p_2\) eines konkurrierenden Produkts \(R\). Die Nachfragefunktion lautet: \[ \begin{gathered} q(p_1,p_2)=400-4p_1+3p_2. \end{gathered} \] Zu berechnen sind die partiellen Preiselastizitäten für aktuelle Preise \(p_1=50\) und \(p_2=30\).
Lösung: Hier bringt das Logarithmieren nicht sehr viel, so dass wir die erste Variante von (8.4) anwenden: \[ \begin{aligned} \epsilon_1(p_1,p_2)&=\frac{q_1'(p_1,p_2)}{q(p_1,p_2)}\cdot p_1 =-\frac{4p_1}{400-4p_1+3p_2},\\[5pt] \epsilon_1(50,30)&=-\frac{200}{290}\simeq -0.69\,. \end{aligned} \] Eine Erhöhung des Preises \(p_1\) um 1 % würde bei unverändertem Preis \(p_2\) einen Rückgang der Nachfrage um ca. 0.69 % bewirken.
Nun die Kreuzpreiselastizität: \[ \begin{aligned} \epsilon_2(p_1,p_2)&=\frac{q_2'(p_1,p_2)}{q(p_1,p_2)}\cdot p_2 =\frac{3p_2}{400-4p_1+3p_2},\\[5pt] \epsilon_2(50,30)&=\frac{90}{290}\simeq 0.31\,.\end{aligned} \] Die beiden Güter sind also substitutiv. □
8.4.5 Eine erste Variante der Kettenregel
Wir haben mit Hilfe der Idee der Richtungsableitung das Konzept der partiellen Ableitungen einer Funktion in zwei Variablen entwickelt. Dies geschah einfach mittels Spezialisierung des Verschiebungsvektors \(\mathbf v\) durch seine Ausrichtung parallel zu einer der Koordinatenachsen.
Aber geht es auch umgekehrt? Können wir bei bekannten ersten partiellen Ableitungen \(\boldsymbol{f}'(\mathbf x)\) für irgendein \(\mathbf v\) die Richtungsableitung bestimmen?
Die Antwort liefert der folgende Satz, den wir aber nicht beweisen werden:
Satz 8.25 Es sei \(f\) eine Funktion mit zwei Variablen, die stetige partielle Ableitungen besitzt. Weiters sei \(\mathbf x=\mathbf a+t\mathbf v\) eine gleichförmige Bewegung und \(c(t)=f(\mathbf a+t\mathbf v)\) der Verlauf der Funktion \(f\) entlang dieser gleichförmigen Bewegung. Die erste Ableitung \(c'(0)\) ist gegeben durch: \[ \begin{gathered} c'(0)= f'_1(\mathbf a)v_1+f'_2(\mathbf a)v_2={\mathbf v}^\top \cdot \boldsymbol{f}'(\mathbf a). \end{gathered} \] Das ist das Matrixprodukt des transponierten Verschiebungsvektors mit dem Gradienten.
Beachten Sie bitte, dass dieser Satz ausdrücklich die Ableitung von \(c(t)\) für \(t=0\) liefert, d.h. also im Punkt \(\mathbf x=\mathbf a\).
Im folgenden Beispiel untersuchen wir eine interessante Anwendung von Satz 8.25.
Bisher haben wir stets angenommen, dass die Nachfrage nach einem Gut lediglich von dessen Preis, eventuell von Preisen konkurrierender Produkte abhängt. Aber gerade bei langlebigen Konsumgütern hängt die Nachfrage auch vom Einkommen ab: je höher das Einkommen, desto größer ist die Nachfrage nach gewissen Gütern.
Musteraufgabe 8.26 Die nachgefragte Menge \(q\) eines langlebigen Konsumguts hängt vom Einkommen \(m\) und dem Preis \(p\) ab auf folgende Weise: \[ \begin{gathered} q(m,p)=\frac{0.2m^2}{10+3p}. \end{gathered} \] Aus statistischen Untersuchungen ist bekannt, dass sowohl \(m\) als auch \(p\) linear mit der Zeit zunehmen, und zwar: \[ \begin{gathered} \begin{array}{rcl} m(t)&=&1000+0.1t\\ p(t)&=&500+0.04t \end{array},\qquad t\ge 0\quad\text{(in Jahren)}. \end{gathered} \] Zu berechnen ist die gegenwärtige (\(t=0)\) Änderungsrate der Nachfrage als Funktion der Zeit.
Lösung: Die Nachfrage ist eine Funktion der Zeit: \[ \begin{gathered} c(t)=q(m(t),p(t))=\frac{0.2(1000+0.1t)^2}{10+3(500+0.04t)}. \end{gathered} \] Um \(c'(0)\) zu berechnen, wenden wir Satz 8.25 an. Das lineare Wachstum von Preis und Einkommen gibt Anlass zu einer gleichförmigen Bewegung in der \((m,p)-\)Ebene: \[ \begin{gathered} \left(\begin{array}{c} m(t)\\ p(t) \end{array} \right)=\left(\begin{array}{c}1000\\500\end{array}\right)+t\left(\begin{array}{r}0.1\\0.04 \end{array}\right). \end{gathered} \] Der Verschiebungsvektor ist \({\mathbf v}^\top =(0.1,0.04)\). Nun benötigen wir noch den Vektor der ersten partiellen Ableitungen, den Gradienten der Funktion \(q(m,t)\), sowie die Werte dieser Ableitungen für \(t=0\), d.h. für \(m=1000\) und \(p=500\): \[ \begin{gathered} \begin{array}{rclcrcl} q_1'(m,p)&=&\dfrac{0.4m}{10+3p} && q_1'(1000,500)&=&0.2649,\\[10pt] q_2'(m,p)&=&-\dfrac{0.6m^2}{(10+3p)^2} &&q_2'(1000,500)&=&-0.2631. \end{array} \end{gathered} \] Die momentane Änderungsrate der Nachfrage beträgt daher: \[ \begin{gathered} c'(0)=(0.1,0.04)\left(\begin{array}{r}0.2649\\-0.2631 \end{array} \right)=0.0160\,. \end{gathered} \] □
8.5 Partielle Ableitungen zweiter Ordnung
Alle bisherigen Beispiele haben uns gezeigt, dass die ersten partiellen Ableitungen einer Funktion \(f(x,y)\) selber wieder Funktionen von \(x\) und \(y\) waren. Wir können daher versuchen, jede dieser Ableitungen erneut nach \(x\) und \(y\) partiell zu differenzieren. Dabei haben wir insgesamt vier Möglichkeiten, diese zweiten partiellen Ableitungen zu bilden. Die Symbolik wird nun etwas komplizierter. Wir schreiben: \[ \begin{gathered} \begin{array}{ll} f_{11}''(x,y)=\dfrac{\partial}{\partial x}\left(\dfrac{\partial f}{\partial x}\right)=\dfrac{\partial^2f}{\partial x^2}& f_{12}''(x,y)=\dfrac{\partial}{\partial x}\left(\dfrac{\partial f}{\partial y}\right)=\dfrac{\partial^2f}{\partial x\partial y}\\[12pt] f_{21}''(x,y)=\dfrac{\partial}{\partial y}\left(\dfrac{\partial f}{\partial x}\right)=\dfrac{\partial^2f}{\partial y\partial x}& f_{22}''(x,y)=\dfrac{\partial}{\partial y}\left(\dfrac{\partial f}{\partial y}\right)=\dfrac{\partial^2f}{\partial y^2} \end{array} \end{gathered} \] Ein Wort zur Schreibweise: \[ \begin{gathered} \frac{\partial}{\partial x}\quad\text{bzw.}\quad \frac{\partial}{\partial y} \end{gathered} \] nennt man einen Differentialoperator. Damit meint man die Aufforderung, das, worauf dieser Operator angewendet wird, partiell nach \(x\) bzw. \(y\) zu differenzieren.
Das Symbol \(f_{11}''(x,y)\) bedeutet: differenziere die erste Ableitung nach \(x\), also \(f_1'(x,y)\), erneut nach \(x\). Dies kommt in der Operatorschreibweise besonders klar zum Ausdruck.
Analog: \(f_{22}''(x,y)\) bedeutet, zweimal hintereinander \(f(x,y)\) partiell nach \(y\) abzuleiten.
Die anderen beiden Symbole bezeichnen gemischte Ableitungen.
\(f_{12}''(x,y)\) bedeutet: differenziere \(f(x,y)\) zuerst nach \(y\) und anschließend nach \(x\). Bei \(f_{21}''(x,y)\) ist es genau umgekehrt.
Es gibt also vier zweite Ableitungen, doch müssen wir in den meisten Fällen nur drei berechnen, denn wenn die gemischten Ableitungen stetig sind, dann sind sie gleich, also \(f_{12}''(x,y)=f_{21}''(x,y)\), es kommt also nicht auf die Reihenfolge des Differenzierens an.
Ähnlich, wie wir die ersten Ableitungen zu einem Vektor zusammengefasst haben, den Gradienten, fassen wir die zweiten Ableitungen in einer Matrix zusammen, die Hesse-Matrix der Funktion \(f(x,y)\): \[ \begin{gathered} \boldsymbol{f}''(x,y)=\left(\begin{array}{cc} f_{11}''(x,y) & f_{12}''(x,y)\\ f_{21}''(x,y) & f_{22}''(x,y) \end{array} \right), \end{gathered} \] oder wir schreiben dafür auch völlig gleichbedeutend: \[ \begin{gathered} \boldsymbol{f}''(\mathbf x)=\left(\begin{array}{cc} f_{11}''(\mathbf x) & f_{12}''(\mathbf x)\\ f_{21}''(\mathbf x) & f_{22}''(\mathbf x) \end{array} \right). \end{gathered} \]
Musteraufgabe 8.27 Bestimme die Hesse-Matrix der Funktion \(f(x,y)=2xy^3-y^2+5x-7\) im Punkt \({\mathbf a}^\top =(1,\,2)\).
Lösung: Zuerst berechnen wir die ersten partiellen Ableitungen nach \(x\) und \(y\): \[ \begin{gathered} f_1'(x,y)=2y^3+5,\qquad f_2'(x,y)=6xy^2-2y. \end{gathered} \] Nun nacheinander: \[ \begin{gathered} f_{11}''(x,y)=\frac{\partial}{\partial x}(2y^3+5)=0, \end{gathered} \] das muss Null sein, weil wir nach \(x\) differenzieren und \(2y^3+5\) daher konstant ist. \[ \begin{gathered} f_{22}''(x,y)=\frac{\partial}{\partial y}(6xy^2-2y)=12xy-2. \end{gathered} \] Für die gemischten Ableitungen erhalten wir: \[ \begin{aligned} f_{12}''(x,y)&=\frac{\partial}{\partial x}(6xy^2-2y)=6y^2,\\[5pt] f_{21}''(x,y)&=\frac{\partial}{\partial y}(2y^3+5)=6y^2=f_{12}''(x,y). \end{aligned} \] Damit haben wir die Hesse-Matrix: \[ \begin{gathered} \boldsymbol{f}''(x,y)=\left(\begin{array}{cc} 0 & 6y^2\\6y^2 &12xy-2 \end{array} \right),\qquad \boldsymbol{f}''(1,2)=\left(\begin{array}{cc} 0 & 24\\24 &22 \end{array} \right). \end{gathered} \] □
Musteraufgabe 8.28 Gesucht ist die Hesse-Matrix von \(f(x,y)=x/y\) im Punkt \({\mathbf a}^\top =(1,-1)\).
Lösung: Die ersten partiellen Ableitungen sind: \[ \begin{gathered} f_1'(x,y)=\frac{1}{y},\qquad f_2'(x,y)=-\frac{x}{y^2}. \end{gathered} \] Weiter: \[ \begin{gathered} f_{11}''(x,y)=\frac{\partial}{\partial x}\frac{1}{y}=0,\quad f_{22}''(x,y)=\frac{\partial}{\partial y}\left(-\frac{x}{y^2}\right) = \frac{2x}{y^3}, \end{gathered} \] sowie \[ \begin{gathered} f_{12}''(x,y)=\frac{\partial}{\partial x}\left(-\frac{x}{y^2}\right) =-\frac{1}{y^2}=f_{21}''(x,y). \end{gathered} \] Daher lautet die Hesse-Matrix: \[ \begin{gathered} \boldsymbol{f}''(x,y)=\left(\begin{array}{rr} 0 & -\dfrac{1}{y^2}\\[10pt] -\dfrac{1}{y^2} & \dfrac{2x}{y^3} \end{array} \right),\qquad \boldsymbol{f}''(1,-1)=\left(\begin{array}{rr} 0 & -1\\-1 & -2 \end{array} \right). \end{gathered} \] □
8.5.1 Die zweite Ableitung einer quadratischen Funktion
Bei der Herleitung von Satz 8.20 haben wir bereits herausgefunden: ist \(g(x,y)=a_{11}x^2+2a_{12}xy+a_{22}y^2\) eine homogene quadratische Funktion, so gilt: \[ \begin{gathered} \left. \begin{array}{rcl} g_1'(x,y)&=&2a_{11}x+2a_{12}y\\[5pt] g_2'(x,y)&=&2a_{12}x+2a_{22}y \end{array}\right\}\implies \boldsymbol{g}'(\mathbf x)=2\mathbf A\mathbf x.\qquad \mbox{(A)} \end{gathered} \] Nun bilden wir in (A) die zweiten partiellen Ableitungen: \[ \begin{gathered} \left. \begin{array}{rclcrcl} g_{11}''(x,y)&=&2a_{11} && g_{12}''(x,y)&=&2a_{12}\\[5pt] g_{21}''(x,y)&=&2a_{12} && g_{22}''(x,y)&=&2a_{22} \end{array}\right\}\implies \boldsymbol{g}''(\mathbf x)=2\mathbf A \end{gathered} \] Daraus ergibt sich zwanglos das wichtige Ergebnis:
Satz 8.29 (Zweite Ableitung einer quadratischen Funktion) Es sei \[ \begin{gathered} f(\mathbf x)={\mathbf x}^\top \mathbf A \mathbf x+{\mathbf b}^\top \mathbf x+c \end{gathered} \] eine allgemeine quadratische Funktion. Dann ist ihre zweite Ableitung: \[ \begin{gathered} \boldsymbol{f}''(\mathbf x)=2\mathbf A \end{gathered} \]
Beachten Sie die schöne Analogie zu quadratischen Funktionen in einer Variablen \(y=ax^2+bx+c\). Ihre zweite Ableitung ist ja \(y''=2a\).
8.5.2 Die zweite Ableitung in eine Richtung
Das folgende Ergebnis wird sich bei unserem nächsten Unternehmen, Optimierung von Funktionen in zwei Variablen, als außerordentlich wichtig erweisen.
Erneut betrachten wir einen geradlinigen Vertikalschnitt \(c(t)\) entlang \(\mathbf x=\mathbf a+t\mathbf v, \mathbf v\ne \boldsymbol{0}\) durch das Funktionsgebirge. Nun interessiert uns der Wert der 2. Ableitung \(c''(0)\). Wenn nämlich \(c'(0)=0\) ist, dann liegt in \(t=0\), also im Punkt \(\mathbf x=\mathbf a\), ein kritischer Punkt der Schnittkurve \(c(t)\), und wir wissen aus Kapitel 3, dass wir die Entscheidung darüber, ob dieser kritische Punkt ein Maximum oder ein Minimum ist, herbeiführend können über das Vorzeichen der 2. Ableitung. Der folgende Satz, in dem die Hesse-Matrix eine Schlüsselrolle spielt, ist tatsächlich ebenfalls eine Variante der Kettenregel wie Satz 8.25.
Satz 8.30 Es sei \(f\) eine Funktion mit zwei Variablen, die stetige zweite partielle Ableitungen besitzt. Weiters sei \(\mathbf x=\mathbf a+t\mathbf v\) eine gleichförmige Bewegung und \(c(t)=f(\mathbf a+t\mathbf v)\). Dann ist die 2. Ableitung der Schnittkurve \(c(t)\) für \(t=0\), d.h. im Punkt \(\mathbf x=\mathbf a\): \[ \begin{aligned} c''(0)&= f''_{11}(\mathbf a)v_1^2+2f''_{12}(\mathbf a)v_1v_2+f''_{22}(\mathbf a)v_2^2\\[5pt] &= (v_1,v_2)\left(\begin{array}{cc} f_{11}''(\mathbf a) & f_{12}''(\mathbf a) \\[4pt] f_{21}''(\mathbf a) & f_{22}''(\mathbf a) \end{array} \right)\left(\begin{array}{c}v_1\\v_2\end{array}\right)={\mathbf v}^\top \boldsymbol{f}''(\mathbf a) \mathbf v. \end{aligned} \] Dies ist die von der Hesse-Matrix im Punkt \(\mathbf a\) erzeugte homogene quadratische Funktion.
8.6 Globale Optimierung
In diesem Abschnitt begeben wir uns auf die Suche nach Extremwerten einer Funktion \(f(x,y)\) mit zwei Variablen. Zur Erinnerung, in Kapitel 3 formulierten wir für Funktionen in einer Variablen die Regel:
Es sei \(x_0\) ein kritischer Punkt einer Funktion \(f(x)\), d.h. \(f'(x_0)=0\). Dieser Punkt ist ein relatives Maximum, wenn \(f''(x_0)<0\), und ein relatives Minimum, wenn \(f''(x_0)>0\).
Wir werden feststellen, dass die Verhältnisse für Funktionen in zwei Variablen nicht so grundsätzlich anders sind. Allerdings werden unsere Ergebnisse allgemeiner sein als in Kapitel 3, wo wir uns auf relative, d.h. lokale Extremwerte beschränkt haben. Nun suchen wir globale Extremstellen einer Funktion.
8.6.1 Kritische Punkte
Es sei \(f:M\to\mathbb R\), \(M\subseteq\mathbb R^2\), eine differenzierbare Funktion mit zwei Variablen.
Ein Punkt \(\mathbf a\in M\) ist ein globales Maximum von \(f\), wenn \[ \begin{gathered} f(\mathbf x)\le f(\mathbf a)\quad\text{für alle $\mathbf x\in M$}. \end{gathered} \] Ein Punkt \(\mathbf a\in M\) ist ein globales Minimum von \(f\), wenn \[ \begin{gathered} f(\mathbf x)\ge f(\mathbf a)\quad\text{für alle $\mathbf x\in M$}. \end{gathered} \] Es ist ganz einfach, eine Bedingung (Gleichung) anzugeben, die von jedem globalen Maximum oder globalen Minimum erfüllt sein muss.
Satz 8.31 Es sei \(f\) eine Funktion mit zwei Variablen und einer stetigen Ableitung, und es sei \(\mathbf a\) ein innerer Punkt von \(M\).
Wenn der Punkt \(\mathbf a\) ein globales Maximum oder ein globales Minimum von \(f\) ist, dann muss \(\mathbf a\) ein kritischer Punkt von \(f\) sein, dh. es muss die Gleichung \[ \begin{gathered} f'(\mathbf a)=\boldsymbol{0} \end{gathered} \] erfüllt sein.
Mit anderen Worten: An einem globalen Maximum oder globalen Minimum einer Funktion sind alle partiellen Ableitungen erster Ordnung gleich Null.
Begründung: Wenn \(\mathbf a\) ein globales Maximum von \(f\) ist, dann ist \(\mathbf a\) auch ein Maximum von \(f\) entlang einer gleichförmigen Bewegung \(\mathbf x=\mathbf a+t\mathbf v\) mit jedem beliebigen Verschiebungsvektor \(\mathbf v\ne \boldsymbol{0}\). Daher hat \(c(t)=f(\mathbf a+t\mathbf v)\) ein Maximum an der Stelle \(t=0\), und es folgt aus Satz 8.25: \[ \begin{gathered} 0=c'(0)={\mathbf v}^\top \cdot \boldsymbol{f}'(\mathbf a)=f'_1(\mathbf a)v_1+f'_2(\mathbf a)v_2 \end{gathered} \] für jeden beliebigen Verschiebungsvektor \(\mathbf v\ne \boldsymbol{0}\). Das ist aber nur möglich, wenn beide partiellen Ableitungen \(f'_1(\mathbf a)\) und \(f'_2(\mathbf a)\) gleich Null sind.
Ein analoges Argument wendet man bei einem globalen Minimum an. □
Jedes Optimum ist also ein kritischer Punkt und kritische Punkte kann man als Lösungen von Gleichungen gewinnen.
8.6.2 Konvexe Funktionen
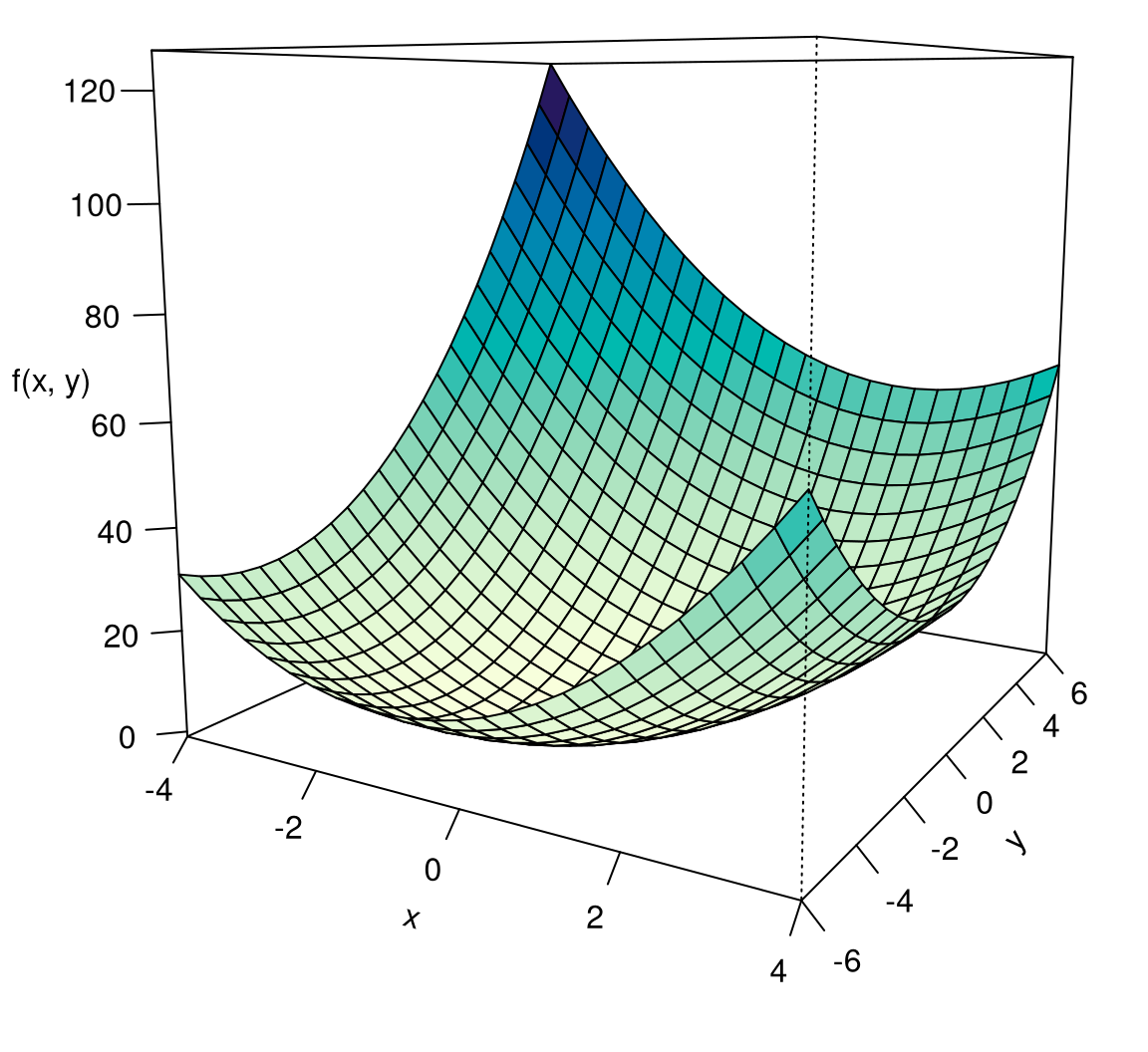
Musteraufgabe 8.32 Man finde ein globales Minimum der quadratischen Funktion \[ \begin{gathered} f(x,y)=2x^2-xy+y^2-2x+4y+3. \end{gathered} \] Sie ist in Abbildung 8.10 dargestellt.
Lösung: Wenn die Funktion überhaupt ein globales Minimum besitzt, muss es ein kritischer Punkt sein. Wir berechnen daher die partiellen Ableitungen \[ \begin{gathered} f'_1(x,y)=4x-y-2,\quad f'_2(x,y)=-x+2y+4, \end{gathered} \] und lösen das Gleichungssystem \(f'_1=0\), \(f'_2=0\), dh. \[ \begin{aligned} 4x-y-2&=0\\ -x+2y+4&=0 \end{aligned} \] Die Lösung lautet \(x=0\), \(y=-2\), also ist der einzige kritische Punkt von \(f(x,y)\) der Punkt \({\mathbf a}^\top =(0,-2)\).
Wenn daher die Funktion \(f(x,y)\) ein globales Minimum besitzt, dann kommt dafür nur der Punkt \(\mathbf a\) in Frage.
Wie können wir aber sicher sein, dass der Punkt \(\mathbf a\) wirklich ein globales Minimum ist?
Zu diesem Zweck untersuchen wir die zweite Ableitung von \(f\).
Die Hesse-Matrix von \(f\) lautet: \[ \begin{gathered} \boldsymbol{f}''(x,y)=\left(\begin{array}{rr}4 & -1\\-1 & 2\end{array}\right). \end{gathered} \] Nun betrachten wir gleichförmige Bewegungen in der \((x,y)-\)Ebene, die allesamt durch den kritischen Punkt \(\mathbf a\) verlaufen und einen ganz beliebigen Verschiebungsvektor \(\mathbf v\ne \boldsymbol{0}\) besitzen. Mit anderen Worten: wir führen Vertikalschnitte durch den Punkt \(\mathbf a\), die Richtung jedes Schnitts ist \(\mathbf v\). Jeder dieser Schnitte liefert eine Randkurve \(c(t)\).
Wenn nun \(\mathbf a\) tatsächlich ein globales Minimum von \(f(x,y)\) ist, dann muss \(\mathbf a\) nicht nur kritischer Punkt von jedem \(c(t)\) sein, es muss auch ein Minimum auf jedem \(c(t)\) sein, das bedeutet, \(c''(0)\ge 0\).
Das können wir aber mit Satz 8.30 beurteilen: es muss gelten für jedes \(\mathbf v\ne \boldsymbol{0}\): \[ \begin{gathered} {\mathbf v}^\top \boldsymbol{f}''(\mathbf a) \mathbf v={\mathbf v}^\top \left(\begin{array}{rr}4 & -1\\-1 & 2\end{array}\right) \mathbf v\ge 0. \end{gathered} \] Nun schreiben wir (wie unter Abbildung 8.6 beschrieben) diese homogene quadratische Funktion ausführlicher an: \[ \begin{aligned} {\mathbf v}^\top \boldsymbol{f}''(\mathbf a) \mathbf v&=4v_1^2-2v_1v_2+2v_2^2\\[5pt] &=\underbrace{4v_1^2-2v_1v_2+\frac{1}{4}v_2^2}_{}\; \underbrace{-\frac{1}{4}v_2^2+2v_2^2}_{}\\[5pt] &=\left(2v_1-\frac{1}{2}v_2\right)^2+\frac{7}{4}v_2^2\ge 0, \end{aligned} \] Beide Terme (es sind Quadrate!) sind nichtnegativ und damit auch ihre Summe.
Die zweite Ableitung entlang einer beliebigen gleichförmigen Bewegung ist offenbar immer nichtnegativ. Also ist \(\mathbf a\) ein globales Minimum von \(f\) entlang jeder gleichförmigen Bewegung durch \(\mathbf a\) und daher ein globales Minimum schlechthin. □
Wir haben in diesem Beispiel gesehen, dass bei einer Funktion, für die alle zweiten Ableitungen entlang von gleichförmigen Bewegungen \(\mathbf a+t\mathbf v\) nichtnegativ sind, jeder kritische Punkt \(\mathbf a\) ein globales Minimum sein muss.
Wir fassen nun alles zusammen, wobei wir wichtige neue Begriffe einführen.
Definition 8.33 Eine symmetrische Matrix \(\mathbf A\) der Ordnung \(n\times n\) heißt positiv semidefinit, wenn \({\mathbf v}^\top \mathbf A\mathbf v\ge 0\) für alle \(\mathbf v\in\mathbb R^n\).
Definition 8.34 Eine Funktion \(f\) mit zwei Variablen und einer stetigen zweiten Ableitung heißt konvex, wenn ihre Hesse-Matrix überall positiv semidefinit ist.
Die Eigenschaft einer Funktion, konvex zu sein, bedeutet anschaulich, dass ihr Funktionsgraph nach unten gewölbt ist. Abbildung 8.10 zeigt eine konvexe Funktion.
Satz 8.35 Bei einer konvexen Funktion ist jeder kritische Punkt ein globales Minimum.
Bei konvexen Funktionen ist es also besonders einfach, ein globales Minimum zu finden: Es genügt irgendeinen kritischen Punkt zu finden!
Man stellt fest, ob eine Funktion \(f\) konvex ist, indem man nachprüft, ob ihre Hesse-Matrix positiv semidefinit ist. Dabei ist die folgende Regel hilfreich.
Satz 8.36 Eine symmetrische \(2\times 2\)-Matrix \(\mathbf A= \left(\begin{array}{cc}a & b\\b & c\end{array}\right)\) ist genau dann positiv semidefinit, wenn \(a\ge 0, c\ge 0\) und \(\det\mathbf A\ge 0\).
Begründung: Zuerst für den Fall \(a\not=0\). Es ist \[ \begin{aligned} {\mathbf v}^\top \mathbf A\mathbf v&=av_1^2+2bv_1v_2+cv_2^2\\ &=a\Big(v_1+\frac{b}{a}v_2\Big)^2+\Big(c-\frac{b^2}{a}\Big)v^2_2. \end{aligned} \] Das ist genau dann \(\ge 0\) für alle \(v_1,\,v_2\in\mathbb R\), wenn \(a\ge 0\) und \(ac\ge b^2\). Die letztere Bedingung impliziert \(c\ge 0\) und ist auch äquivalent mit \(\det \mathbf A\ge 0\).
Wenn hingegen \(a=0\), dann ist \[ \begin{gathered} {\mathbf v}^\top \mathbf A\mathbf v=2bv_1v_2+cv_2^2, \end{gathered} \] und dieser Ausdruck kann nur dann \(\ge 0\) sein für alle \(\mathbf v\ne \boldsymbol{0}\), wenn \(b=0\) und \(c\ge 0\). Sind aber \(a=0\) und \(b=0\), dann ist auch \(\det\mathbf A=0\). □
Konvexe Funktionen besitzen viele bemerkenswerte Eigenschaften. Unter anderem sind Summen von konvexen Funktionen wieder konvex. Deshalb gilt:
Satz 8.37 Lineare Funktionen \(g(x,y)={\mathbf b}^\top \mathbf x+c\) sind konvex, denn ihre Hesse-Matrix ist die Nullmatrix, und diese ist positiv semidefinit. Wenn \(f(x,y)\) eine konvexe Funktion in zwei Variablen bezeichnet, dann ist \(f(x,y)+{\mathbf b}^\top \mathbf x+c\) wieder konvex.
8.6.3 Konkave Funktionen
Wenn eine Funktion \(f\) konvex ist, so ist \(-f\) konkav, also nach oben gewölbt. Alles was wir über konvexe Funktionen ausgeführt haben, überträgt sich mutatis mutandis auf konkave Funktionen. Wir fassen zusammen:
Definition 8.38 Eine symmetrische Matrix \(\mathbf A\) der Ordnung \(n\times n\) heißt negativ semidefinit, wenn \({\mathbf v}^\top \mathbf A\mathbf v\le 0\) für alle \(\mathbf v\in\mathbb R^n\).
Definition 8.39 Eine Funktion \(f\) mit zwei Variablen und einer stetigen zweiten Ableitung ist konkav, wenn ihre Hesse-Matrix überall negativ semidefinit ist.
Satz 8.40 Bei einer konkaven Funktion ist jeder kritische Punkt ein globales Maximum.
Auch bei konkaven Funktionen ist es also besonders einfach, ein globales Maximum zu finden: finde irgendeinen kritischen Punkt!
Man stellt fest, ob eine Funktion \(f\) konkav ist, indem man nachprüft, ob ihre Hesse-Matrix negativ semidefinit ist. Dabei ist die folgende Regel hilfreich.
Satz 8.41 Eine symmetrische \(2\times 2\)-Matrix \(\mathbf A=\left(\begin{array}{cc}a & b\\b & c\end{array}\right)\) ist genau dann negativ semidefinit, wenn \(a\le 0, c\le 0\) und \(\det\mathbf A\ge 0\).
Begründung: Im Fall \(a\ne 0\): \[ \begin{aligned} {\mathbf v}^\top \mathbf A\mathbf v&=av_1^2+2bv_1v_2+cv_2^2\\[5pt] &=a\Big(v_1+\frac{b}{a}v_2\Big)^2+\Big(c-\frac{b^2}{a}\Big)v^2_2 \end{aligned} \] Das ist genau dann \(\le 0\) für alle \(v_1,\,v_2\in\mathbb R\), wenn \(a\le 0\) und \(c-\frac{b^2}{a}\le 0\), dh. \(ac\ge b^2\). Die letztere Bedingung impliziert (weil \(a\le 0\)), dass \(c\le 0\) und ist äquivalent mit \(\det \mathbf A\ge 0\).
Analog lässt sich der Fall \(a=0\) zeigen. □
Musteraufgabe 8.42 Man finde das Optimum der Funktion \(f(x,y)=e^{-x^2-y^2}\).

Lösung: Zuerst begeben wir uns auf die Suche nach einem kritischen Punkt. Dazu bilden wir die ersten Ableitungen und setzen diese Null:
\[ \begin{gathered} f_1'(x,y)=-2xe^{-x^2-y^2},\quad f_2'(x,y)=-2ye^{-x^2-y^2}. \end{gathered} \] Die Bedingungen \(f_1'(x,y)=0\) und \(f_2'(x,y)=0\) sind nur im Punkt \(x=0,y=0\) erfüllt, denn die Exponentialfunktion ist immer \(>0\). Daher gibt es einen kritischen Punkt, nämlich \({\mathbf a}^\top =(0,0)\).
Nun bilden wir die Hesse-Matrix, dabei ist zu beachten, dass wir für \(f_{11}''(x,y)\) und \(f_{22}''(x,y)\) die Produktregel anwenden müssen: \[ \begin{gathered} \begin{array}{ll} f_{11}''(x,y)=-2(1-2x^2)e^{-x^2-y^2} & f_{12}''(x,y)=4xye^{-x^2-y^2}\\[5pt] f_{21}''(x,y)= 4xye^{-x^2-y^2} & f_{22}''(x,y)=-2(1-2y^2)e^{-x^2-y^2} \end{array} \end{gathered} \] Die Hesse-Matrix und ihr Wert im kritischen Punkt sind daher: \[ \begin{aligned} \boldsymbol{f}''(\mathbf x)&=e^{-x^2-y^2}\left(\begin{array}{cc} -2(1-2x^2) & 4xy\\4xy & -2(1-2y^2) \end{array} \right),\\ \boldsymbol{f}''(0,0)&=\left(\begin{array}{rr}-2 & 0\\0 & -2\end{array}\right). \end{aligned} \] Die Matrix \(\boldsymbol{f}''(0,0)\) ist aber nach Satz 8.41 negativ semidefinit, denn ihre Hauptdiagonalkomponenten sind beide negativ und ihre Determinante hat den Wert \(4>0\). daher ist der Punkt \((0,0)\) ein globales Maximum. □
8.6.4 Quadratische Funktionen
Für quadratische Funktionen \[ \begin{gathered} f(\mathbf x)={\mathbf x}^\top \mathbf A\mathbf x+{\mathbf b}^\top \mathbf x+c,\qquad \mbox{(A)} \end{gathered} \] ist es besonders einfach festzustellen, ob sie konvex oder konkav sind. Nach Satz 8.29 ist ihre Hesse-Matrix \(2\mathbf A\). Wir wenden dann einfach Satz 8.36 oder Satz 8.41 an.
Ist die den homogenen Teil erzeugende Matrix \(\mathbf A\) regulär, d.h. sie besitzt eine Inverse, dann ist das Optimum sogar eindeutig bestimmt. Denn wenn wir (A) differenzieren und die erste Ableitung Null setzen (siehe Satz 8.20) erhalten wir: \[ \begin{gathered} \boldsymbol{f'}(\mathbf x)=2\mathbf A\mathbf x+\mathbf b= \boldsymbol{0}.\qquad \mbox{(B)} \end{gathered} \] Diese Matrixgleichung lösen wir nach \(\mathbf x\) (siehe Kapitel 7): \[ \begin{gathered} \mathbf x=-\frac{1}{2}\mathbf A^{-1}\mathbf b. \end{gathered} \] Ist hingegen \(\mathbf A\) singulär, dann müssen wir uns um die allgemeine Lösung des linearen Gleichungssystems (B) bemühen. Falls es überhaupt eine Lösung hat, dann haben wir gleich unendlich viele kritische Punkte und damit eben soviele Optima!
Musteraufgabe 8.43 Ein Monopolunternehmen bietet zwei Güter zu Preisen \(p_1\) und \(p_2\) an. Die Nachfrage wird durch die Nachfragefunktionen \[ \begin{aligned} D_1(p_1,p_2):&\quad q_1=310-4p_1+p_2\\ D_2(p_1,p_2):&\quad q_2=248+p_1-8p_2 \end{aligned} \] bestimmt. Die variablen Kosten bei der Herstellung der Güter betragen 20 bzw. 14 GE, die Fixkosten seien 10000 GE. Zu welchen Preisen muss angeboten werden, damit maximaler Gewinn erzielt wird?
Lösung: Der Gewinn ist wie üblich die Differenz zwischen Erlösen und Kosten: \[ \begin{aligned} \pi(p_1,p_2)&=p_1q_1+p_2q_2-20q_1-14q_2-10000\\[4pt] &=p_1(310-4p_1+p_2)+p_2(248+p_1-8p_2)-\\[4pt] &\qquad -20(310-4p_1+p_2)-14(248+p_1-8p_2)-10000\\[4pt] &=-4p_1^2+2p_1p_2-8p_2^2+376p_1+340p_2-19762 \end{aligned} \] Das ist eine quadratische Funktion \[ \begin{gathered} \pi(\mathbf p)={\mathbf p}^\top \mathbf A\mathbf p+{\mathbf b}^\top \mathbf p+c,\qquad {\mathbf p}^\top =(p_1,p_2), \end{gathered} \] mit \[ \begin{gathered} \mathbf A=\left(\begin{array}{rr}-4 & 1\\ 1 & -8\end{array}\right), \quad\mathbf b=\left(\begin{array}{c}376\\340\end{array}\right),\quad c=-19672. \end{gathered} \] Die Hesse-Matrix von \(\pi(\mathbf p)\) ist: \[ \begin{gathered} \boldsymbol{\pi}''(\mathbf p)=2\mathbf A=\left( \begin{array}{rr}-8 & 2\\2 & -16\end{array}\right), \end{gathered} \] diese ist sicher negativ semidefinit, denn beide Hauptdiagonalkomponenten sind negativ und \(\det(2\mathbf A)=124\) ist positiv. Daher ist \(\pi(\mathbf p)\) konkav und jeder kritische Punkt ein globales Maximum.
Es gibt tatsächlich nur ein Maximum, denn \(\det\mathbf A=31\ne 0\). \(\mathbf A\) hat daher eine Inverse und somit: \[ \begin{aligned} \mathbf p&=-\frac{1}{2}\mathbf A^{-1}\mathbf b\\[4pt] &=-\frac{1}{2}\,\frac{1}{31}\left(\begin{array}{rr}-8 & -1\\-1 & -4\end{array} \right)\left(\begin{array}{c}376\\340\end{array}\right) =\left(\begin{array}{c}54\\28\end{array}\right). \end{aligned} \] Die Preissetzung \(p_1=54, p_2=28\) garantiert maximalen Gewinn. □
8.7 Kettenregel und implizite Funktionen
8.7.1 Die Kettenregel
Es sei \(f:M\to\mathbb R\), \(M\subseteq\mathbb R^2\), eine Funktion in zwei Variablen.
Bisher haben wir den Verlauf der Funktion \(f(x,y)\) entlang einer gleichförmigen Bewegung \[ \begin{gathered} \mathbf x=\mathbf g(t)=\mathbf a+t\mathbf v,\;\text{das heißt:}\; \left\{ \begin{array}{l} x=g_1(t)=a_1+tv_1\\ y=g_2(t)=a_2+tv_2 \end{array} \right. \end{gathered} \] \(t\in\mathbb R\), untersucht. Eine solche gleichförmige Bewegung ist eine vektorwertige Funktion \(\mathbf x=\mathbf g(t)\), deren beide Komponenten \(g_1(t)\) und \(g_2(t)\) lineare Funktionen des Parameters \(t\) sind.
Es kommt jedoch auch vor, dass wir den Verlauf einer Funktion \(f\) entlang einer nichtlinearen Funktion \(\mathbf x=\mathbf g(t)\) untersuchen wollen. Wir nennen eine solche Funktion \(\mathbf x=\mathbf g(t)\) einen Pfad. Eine gleichförmige Bewegung ist also ein spezieller Pfad, der erstens geradlinig verläuft und zweitens mit konstanter Geschwindigkeit durchlaufen wird.
Für jeden Parameterwert \(t\in\mathbb R\) berechnen wir den zugehörigen Punkt \(\mathbf x=\mathbf g(t)\) und dazu den Funktionswert \(f(\mathbf x)=f(x,y)\). Dadurch erhalten wir eine Funktion \[ \begin{gathered} c(t)=f(\mathbf g(t))=f(g_1(t),g_2(t)),\qquad x=g_1(t),\;y=g_2(t). \end{gathered} \] Diese Funktion beschreibt die Funktionswerte von \(f\) entlang des Pfades \(\mathbf x=\mathbf g(t)\).
Musteraufgabe 8.44 Ein Hersteller produziert ein Gut aus zwei Rohstoffen \(A\) und \(B\), wobei die Produktionsfunktion durch \[ \begin{gathered} q=f(x,y)=200x^{0.7}y^{0.3} \end{gathered} \] gegeben ist. Das bedeutet, dass beim Einsatz von \(x\) Tonnen des Rohstoffes \(A\) und \(y\) Tonnen des Rohstoffes \(B\) jeweils \(q=f(x,y)\) Einheiten des Endprodukts anfallen.
Im Moment setzt der Hersteller pro Woche \(20\) Tonnen von \(A\) und \(15\) Tonnen von \(B\) ein. Allerdings sinkt die Zulieferung des Rohstoffes \(A\) pro Woche um 4 Prozent, während die zugelieferte Menge des Rohstoffes \(B\) um 3 Prozent steigt.
Wie entwickeln sich die produzierten Mengen des Endprodukts und wie lautet die momentane relative Änderungsrate?
Lösung: Die Zulieferungen der Rohstoffe \(A\) und \(B\) haben konstante relative Änderungsraten \(c_1=\ln 0.96=-0.0408\) und \(c_2=\ln 1.03=0.0296\). Sie werden daher durch die Exponentialfunktionen \[ \begin{gathered} \mathbf x=\mathbf g(t)=\left\{ \begin{array}{l} g_1(t)=20\cdot 0.96^t=20e^{-0.0408 t}\\[5pt] g_2(t)=15\cdot 1.03^t=15e^{0.0296 t} \end{array} \right. \end{gathered} \] beschrieben. Die vektorwertige Funktion \(\mathbf x=\mathbf g(t)\) ist ein Beispiel für einen nichtlinearen Pfad.
Die produzierte Menge \(q=f(x,y)\) des Endprodukts erhält man, in dem man den Pfad \(\mathbf x=\mathbf g(t)\) in die Produktionsfunktion \(q=f(\mathbf x)\) einsetzt: \[ \begin{aligned} c(t)=f(g_1(t),g_2(t))&=200(20e^{-0.0408 t})^{0.7}(15e^{0.0296 t})^{0.3}\\[4pt] &=200\cdot 20^{0.7}\cdot e^{-0.0408\cdot 0.7t}\cdot 15^{0.3}\cdot e^{0.0296\cdot 0.3t}\\[4pt] &=3669.3 \,e^{-0.0197t}. \end{aligned} \] Daraus folgt für die relative Änderungsrate \[ \begin{gathered} \frac{c'(t)}{c(t)}=-0.0197\;. \end{gathered} \] Die Produktion sinkt also wöchentlich mit der Veränderungsrate von \(1.97\) %. □
Wir können den Berechnungsvorgang der letzten Aufgabe erheblich vereinfachen.
Es sei \(\mathbf x=\mathbf g(t)\) ein differenzierbarer Pfad. Dann nennen wir \[ \begin{gathered} \mathbf g'(t)=\left(\begin{array}{c}g_1'(t)\\g_2'(t) \end{array}\right) \end{gathered} \] den Geschwindigkeitsvektor dieses Pfades. Bei einer gleichförmigen Bewegung \[ \begin{gathered} \mathbf g(t)=\mathbf x=\mathbf a+t\mathbf v=\left\{ \begin{array}{l} a_1+tv_1\\a_2+tv_2 \end{array}\right. \end{gathered} \] ist der Geschwindigkeitsvektor \(\mathbf g'(t)=\left(\begin{array}{c}v_1\\v_2 \end{array}\right)=\mathbf v\) konstant (er hängt nicht vom Parameter \(t\) ab).
Musteraufgabe 8.45 Man bestimme den Geschwindigkeitsvektor von \[ \begin{gathered} \mathbf x=\mathbf g(t)=\left\{ \begin{array}{l} g_1(t)=2-t+7t^2\\ g_2(t)=3(1-e^{-0.2t}) \end{array} \right. \end{gathered} \] an der Stelle \(t=1\).
Lösung: \[ \begin{gathered} g_1'(t)=-1+14t,\quad g_2'(t)=0.6e^{-0.2t},\\[2ex] \mathbf g'(t)=\left(\begin{array}{c} -1+14t\\[1ex]0.6e^{-0.2t} \end{array}\right),\quad \mathbf g'(1)= \left(\begin{array}{c} 13\\[1ex]0.6e^{-0.2} \end{array}\right) = \left(\begin{array}{c} 13\\[1ex]0.4912 \end{array} \right). \end{gathered} \] □
Musteraufgabe 8.46 Man bestimme den Geschwindigkeitsvektor von \[ \begin{gathered} \mathbf x=\mathbf g(t)=\left\{ \begin{array}{l} g_1(t)=20\cdot 0.96^t=20e^{-0.0408 t}\\ g_2(t)=15\cdot 1.03^t=15e^{0.0296 t} \end{array} \right. \end{gathered} \] an der Stelle \(t=2\).
Lösung: \[ \begin{aligned} g_1'(t)&=20 e^{-0.0408t}(-0.0408)=-0.816 e^{-0.0408 t}\\ g_2'(t)&=15 e^{0.0296t}0.0296=0.444e^{0.0296 t} \end{aligned} \] \[ \begin{gathered} \mathbf g'(t)= \left(\begin{array}{c} -0.816 e^{-0.0408 t}\\[1ex]0.444e^{0.0296t} \end{array}\right) \quad \mathbf g'(2)= \left(\begin{array}{r} -0.7521\\[1ex]0.4711 \end{array} \right). \end{gathered} \]
Nun können wir eine allgemeine und übersichtliche Formel für die Berechnung der Ableitung von \(c(t)=f(g_1(t),g_2(t))\) angeben. Diese Formel ist eine Erweiterung der Formel aus Satz 8.25.
Satz 8.47 (Kettenregel) Es sei \(f\) eine Funktion mit zwei Variablen, die stetige partielle Ableitungen besitzt. Weiters sei \(\mathbf x=\mathbf g(t)\) ein differenzierbarer Pfad und \(c(t):=f(\mathbf g(t))\). Dann gilt \[ \begin{gathered} c'(t)= f'_1(\mathbf g(t))g_1'(t)+f'_2(\mathbf g(t))g_2'(t) ={\boldsymbol{f}'(\mathbf g(t))}^\top \cdot\mathbf g'(t). \end{gathered} \]
Diese wichtige Formel besagt, in Worten ausgedrückt:
Um die Ableitung von \(c(t)=f(\mathbf g(t))\) zum Zeitpunkt \(t\) zu berechnen, multipliziere man die (in einen Zeilenvektor transponierte) Ableitung von \(f\) an der Stelle \(\mathbf x=\mathbf g(t)\) mit dem Geschwindigkeitsvektor \(\mathbf g'(t)\).
Musteraufgabe 8.48 Es sei \(f(x,y)=x/y\) und \(\mathbf x=\mathbf g(t)\) mit \(g_1(t)=3\ln t\) und \(g_2(t)=1-t\). Man bestimme \(c'(2)\) für \(c(t)=f(\mathbf g(t))\).
Lösung: Wir wenden die Kettenregel an und berechnen zuerst \[ \begin{gathered} g_1'(t)=\frac{3}{t},\quad\text{und}\quad g_2'(t)=-1. \end{gathered} \] Weiters: \[ \begin{aligned} %% {alignat*}{2} f_1'(x,y)&=\frac{1}{y} &\qquad f_1'(g_1(t),g_2(t))&=\frac{1}{1-t}\\[1ex] f_2'(x,y)&=-\frac{x}{y^2} &\qquad f_2'(g_1(t),g_2(t))&=-\frac{3\ln t}{(1-t)^2} \end{aligned} \] Mit der Kettenregel erhalten wir: \[ \begin{aligned} c'(t)&={\boldsymbol{f}'(\mathbf g(t))}^\top \cdot \mathbf g'(t)= \left(\frac{1}{1-t},-\frac{3\ln t}{(1-t)^2}\right)\cdot \left(\begin{array}{r}\dfrac{3}{t}\\-1 \end{array}\right)\\ &=\frac{3}{t(1-t)}+\frac{3\ln t}{(1-t)^2},\\ c'(2)&=-\frac{3}{2}+3\ln 2=0.5794\,. \end{aligned} \] □
Musteraufgabe 8.49 Es sei \(f(x,y)=2xe^{-3y}\) und \(\mathbf x=\mathbf g(t)\) mit \(g_1(t)=5t^2\) und \(g_2(t)=\ln t\). Man bestimme \(c'(2)\) für \(c(t)=f(\mathbf g(t))\).
Lösung: Wir wenden wieder die Kettenregel an und berechnen: \[ \begin{gathered} g_1'(t)=10t,\quad\text{und}\quad g_2'(t)=\frac{1}{t} \end{gathered} \] Nun bilden wir die partiellen Ableitungen von \(f(\mathbf x)\): \[ \begin{aligned} %% {alignat*}{2} f_1'(x,y)&=2e^{-3y}&\qquad f_1'(g_1(t),g_2(t))&=2e^{-3\ln t}=\frac{2}{t^3}\\[1ex] f_1'(x,y)&=-6xe^{-3y}&\qquad f_2'(g_1(t),g_2(t))&=-30t^2e^{-3\ln t}=-\frac{30}{t}. \end{aligned} \] Das ergibt: \[ \begin{aligned} c'(t)&={\boldsymbol{f}'(\mathbf g(t))}^\top \cdot \mathbf g'(t)= \left(\frac{2}{t^3},-\frac{30}{t}\right)\cdot\left( \begin{array}{c} 10t\\[5pt]\dfrac{1}{t} \end{array}\right)\\ &=-\frac{10}{t^2},\\[5pt] c'(2)&=-\frac{10}{4}=-2.5\,. \end{aligned} \] □
Wir kehren nochmals zurück zu Musteraufgabe 8.26 und untersuchen eine Variante dieser Aufgabe..
Musteraufgabe 8.50 Die nachgefragte Menge \(q\) eines langlebigen Konsumguts hängt ab vom Einkommen \(m\) und dem Preis \(p\) auf folgende Weise: \[ \begin{gathered} q(m,p)=\frac{0.2m^2}{10+3p} \end{gathered} \] Aus statistischen Untersuchungen ist bekannt, dass \(m\) einem logistischen Trend folgt, während \(p\) linear mit der Zeit zunimmt, und zwar: \[ \begin{gathered} \begin{array}{rcl} m(t)&=&\dfrac{4500}{1+e^{-t}}\\[9pt] p(t)&=&500+0.04t \end{array},\qquad t\ge 0\quad\text{(in Jahren)} \end{gathered} \] Zu berechnen ist die gegenwärtige (\(t=0)\) Änderungsrate der Nachfrage als Funktion der Zeit.
Lösung: Der Pfad ist \({\mathbf g(t)}^\top =(m(t),p(t))\). Wir berechnen zuerst die Ableitungen von \(m(t)\) und \(p(t)\), d.h. den Geschwindigkeitsvektor: \[ \begin{gathered} \left.\begin{array}{rclcrcl} m'(t)&=&\dfrac{4500 e^{-t}}{(1+e^{-t})^2},&& m'(0)&=&1125\\[10pt] p'(t)&=&0.04,&& p'(0)&=&0.04 \end{array}\right\}\quad \mathbf g'(0)=\left(\begin{array}{r}1125\\0.04\end{array}\right). \end{gathered} \] Als Nächstes die Werte von \(m(t)\) und \(p(t)\) an der Stelle \(t=0\): \[ \begin{gathered} m:=m(0)=\frac{4500}{2}=2250,\quad p:=p(0)=500. \end{gathered} \] Nun benötigen wir die ersten partiellen Ableitungen der Nachfragefunktion: \[ \begin{gathered} \left.\begin{array}{rclcrcl} q_1'(m,p)&=&\dfrac{0.4m}{10+3p},&&q_1'(2250,500)&=&0.5960\\[8pt] q_2'(m,p)&=&-\dfrac{0.6m^2}{(10+3p)^2},&& q_2'(2250,500)&=&-1.3322 \end{array}\right\}\\[5pt] \mathbf q'(\mathbf g(0))=\mathbf q'(2250,500)= \left(\begin{array}{r}0.5960\\-1.3322 \end{array}\right) \end{gathered} \] Daher: \[ \begin{gathered} c'(0)={\mathbf q'(\mathbf g(0))}^\top \cdot \mathbf g(0) =\left(0.5960,\, -1.3322\right)\left(\begin{array}{r}1125\\0.04\end{array}\right) =670.4467\,. \end{gathered} \] □
8.7.2 Implizite Funktionen
Ein Hersteller produziert ein Gut unter Verwendung von zwei Faktoren \(A\) und \(B\). \(A\) könnte etwa ein bestimmtes Rohmaterial sein, \(B\) die Verwendung einer besonderen Maschine. Das Mengengerüst der Produktion ist durch eine Produktionsfunktion repräsentiert. In unserem Fall lautet diese: \[ \begin{gathered} q=F(x,y)=100xy\;. \end{gathered} \] Die Produktionsfunktion bedeutet: Wenn vom Rohmaterial \(A\) \(x\) ME und vom Faktor \(B\) \(y\) Stunden Maschinenzeit aufgewendet werden, so beträgt die produzierte Menge des Gutes \(q=F(x,y)\). Der Herstellungsprozess befindet sich dann auf dem Outputniveau \(q\).
Der Hersteller möchte nun die Faktorkombination ändern, und zwar so, dass das Produktionsniveau (die produzierte Menge \(q\)) dabei nicht verändert wird. Diesen Vorgang nennt man Faktorsubstitution. Es ist klar: bei der gegebenen Produktionsfunktion bewirkt eine Verringerung der eingesetzten Menge des Faktors \(A\) eine Erhöhung der einzusetzenden Menge des Faktors \(B\), und umgekehrt.
Aber warum sollte ein Unternehmen Produktionsfaktoren gegeneinander substituieren?
Produktionsfaktoren müssen auf Faktormärkten erworben werden. Sie haben Preise. Damit stellt sich die naheliegende Frage: Was ist die kostengünstigste Faktorkombination, um einen bestimmten Output \(q\) zu produzieren?
Nehmen wir an, der Hersteller möchte die Menge des Faktors \(A\) festlegen und dann die erforderliche Menge des Faktors \(B\) so berechnen, dass das Produktionsniveau \(q\) gleich bleibt. Bezeichnet man mit \(x=t\) die Menge des Faktors \(A\) und mit \(y=f(t)\) die Menge des Faktors \(B\), dann muss die Gleichung \[ \begin{gathered} q=F(x,y)=F(t,f(t))=100\,t\,f(t) \end{gathered} \] erfüllt ein. Die Definition des Funktionsterms \(f(t)\) nennt man eine implizite Definition (ungenau: eine implizite Funktion), da sie durch eine Gleichung \[ \begin{gathered} q=F(t,f(t)) \end{gathered} \] und nicht durch explizite Angabe des Funktionsterms \(f(t)\) gegeben ist.
Natürlich können wir in unserem einfachen Beispiel den Term \(f(t)\) sofort ausrechnen und damit die Funktion explizit angeben: \[ \begin{gathered} f(t)=\frac{q}{100 t}\;. \end{gathered} \] Technisch gesehen ist \(f(t)\) nichts anderes als eine Niveaulinie der Produktionsfunktion, nämlich genau jene auf der Höhe \(q\). Mikroökonomen nennen diese Niveauline eine Isoquante der Produktionsfunktion. Aus ihr ist das Austauschverhältnis der eingesetzten Produktionsfaktoren bei einem bestimmten Outputniveau bestimmbar.
Für unser Beispiel ist die Situation in Abbildung 8.12 illustriert.
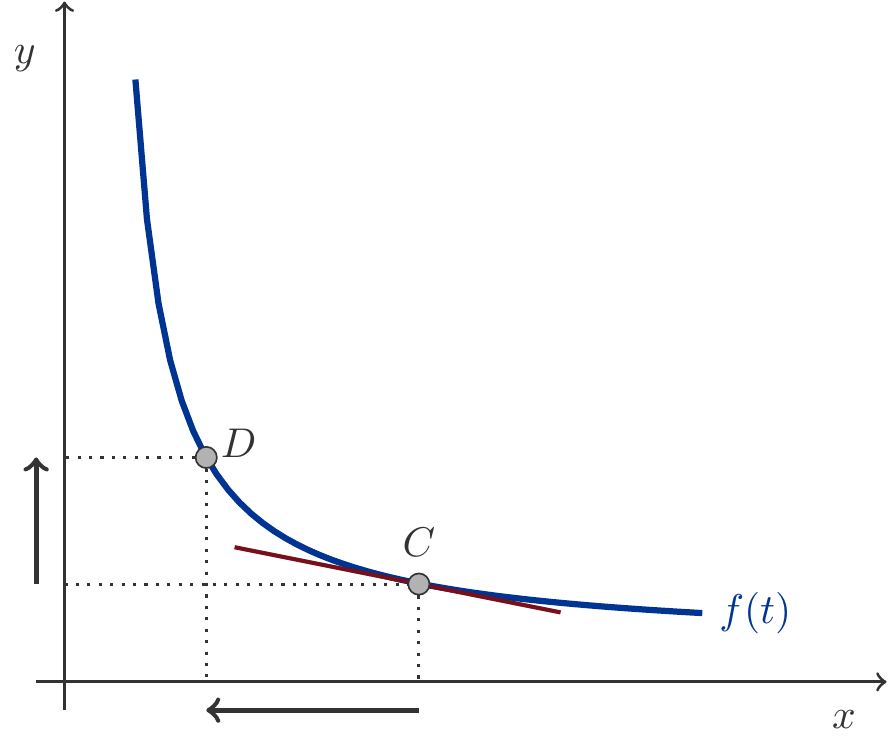
Wenn wir uns auf der Isoquante vom Punkt \(C\) zum Punkt \(D\) bewegen, so substituieren wir eine gewisse Menge des Faktors \(A\) durch den Faktor \(B\) bei unverändertem Output. Aus dem Vergleich der Längen des horizontalen und des vertikalen Pfeiles erkennen wird, dass eine Erhöhung des Faktors \(B\) (vertikaler Pfeil), d.h. ein Mehreinsatz an Maschinenzeit, eine deutlich stärkere Reduktion im Einsatz von Faktor \(A\) bedeutet (horizontaler Pfeil). Zusätzliche Maschinenzeit ergibt eine überproportionale Einsparung an Rohmaterial bei gleichbleibendem Output.
Uns interessiert die marginale Änderung der Faktoreinsatzmengen. Sie ist nichts anderes als die Steigung \(f'(t)\) der Tangente in einem Punkt der Isoquante. Ihr Absolutbetrag heißt Grenzrate der Substitution RTS.
Musteraufgabe 8.52 Es sei \(F(x,y)=2x-y+6\).
Man bestimme die explizite Definition der Funktion \(y=f(t)\), die durch die Gleichung \(F(t,f(t))=-3\) implizit definiert ist.
Man berechne die erste und die zweite Ableitung der Funktion \(f(t)\).
Lösung: Wir setzen \(x=t\) und \(y=f(t)\) und setzen das in \(F(x,y)\) ein: \[ \begin{gathered} F(x,y) =F(t,f(t))=2t-f(t)+6=-3, \\[1ex] \implies f(t)=2t+9,\qquad f'(t)=2,\quad f''(t)=0. \end{gathered} \] □
Musteraufgabe 8.53 Es sei \(F(x,y)=20 x^{0.3}y^{0.6}\).
Man bestimme die explizite Definition der Funktion \(f(t)\), die durch die Gleichung \(F(t,f(t))=2\) implizit definiert ist.
Man berechne die erste und die zweite Ableitung der Funktion \(y=f(t)\).
Lösung: Die Gleichung \[ \begin{gathered} F(t,f(t))= 20t^{0.3}f(t)^{0.6}=2 \end{gathered} \] wird gelöst durch \[ \begin{gathered} f(t)^{0.6}=\frac{2}{20t^{0.3}}=0.1\cdot t^{-0.3}. \end{gathered} \] und daher \[ \begin{gathered} f(t)=\left(0.1\cdot t^{-0.3}\right)^{1/0.6}= 0.0215\cdot t^{-0.5}=\frac{0.0215}{\sqrt{t}}. \end{gathered} \] Die Ableitungen lauten \[ \begin{gathered} f'(t)=-\frac{0.01075}{t\sqrt{t}},\quad f''(t)=\frac{0.016125}{t^2\sqrt{t}}\,. \end{gathered} \] □
Am folgenden Beispiel erkennt man, dass es manchmal ein wenig mühevoll sein kann, die explizite Form einer implizit definierten Funktion zu bestimmen.
Musteraufgabe 8.54 Die Produktionsfunktion laute \(F(x,y)=x^2+5xy+y^2\). Im Moment verwendet der Hersteller die Faktorkombination \((x,y)=(3,5)\). Es soll nun der Einsatz von Faktor \(A\) erhöht und der Einsatz von Faktor \(B\) verringert werden, und zwar unter Beibehaltung des aktuellen Produktionsniveaus.
Berechnen Sie die Grenzrate der Substitution von Faktor \(A\) gegen Faktor \(B\).
Lösung: Das Produktionsniveau beträgt \(F(3,5)=109\). Wir bezeichnen die Faktormenge \(A\) mit \(t\) und die Faktormenge \(B\) mit \(f(t)\).
Die Grenzrate der Substitution ist die erste Ableitung der Funktion \(f(t)\), die implizit durch die Gleichung \[ \begin{gathered} F(t,f(t))=F(3,5)=109 \end{gathered} \] definiert ist, und zwar an der Stelle \(t=3\).
Wir lösen diese Aufgabe hier dadurch, dass wir die explizite Form der Funktion \(y=f(t)\) bestimmen. Es ist \[ \begin{gathered} F(t,f(t))=t^2+5tf(t)+f^2(t)=109, \end{gathered} \] dh. wir erhalten die quadratische Gleichung \[ \begin{gathered} f^2(t)+ 5tf(t)+t^2-109=0, \end{gathered} \] die wir nach \(f(t)\) auflösen müssen. Dies ergibt \[ \begin{gathered} f(t)=\frac{-5t+\sqrt{25t^2-4(t^2-109)}}{2}= \frac{\sqrt{436+21t^2}-5t}{2}. \end{gathered} \] Wir sind nur an positiven Lösungen interessiert. Die Ableitung lautet \[ \begin{gathered} f'(t)=\frac{1}{2}\Big(\frac{21t}{\sqrt{436+21t^2}}-5\Big) \end{gathered} \] Durch Einsetzen von \(t=3\) erhält man die Grenzrate der Substitution für \(t=3\): \[ \begin{gathered} f'(3)=-1.24\implies \text{RTS}=|f'(3)|=1.24\,. \end{gathered} \] Die Antwort lautet also: Wenn der Faktor \(A\) um eine Mengeneinheit erhöht wird, muss der Faktor B um ca. 1.24 Einheiten verringert werden, um das Produktionsniveau beizubehalten. □
Es gibt auch eine einfachere Lösung. Wir differenzieren die Funktion \[ \begin{gathered} c(t)=F(t,f(t)) \end{gathered} \] nach der Kettenregel (Satz 8.47). Als Pfad nehmen wir: \[ \begin{gathered} \mathbf g(t)=\left(\begin{array}{c}t\\f(t)\end{array}\right), \quad \mathbf g'(t)=\left(\begin{array}{c}1\\f'(t)\end{array}\right). \end{gathered} \] Die Kettenregel liefert dann: \[ \begin{gathered} c'(t)=F'_1(t,f(t))\cdot 1+F'_2(t,f(t))\,f'(t)\;. \end{gathered} \] Da die implizite Funktion \(f(t)\) so definiert ist, dass \(c(t)\) konstant ist (im Beispiel das Produktionsniveau \(109\)), muss \(c'(t)\equiv 0\) sein. Daraus folgt die Formel \[ \begin{gathered} f'(t)=-\frac{F'_1(t,f(t))}{F'_2(t,f(t))}\,. \end{gathered} \] Um die Ableitung einer impliziten Funktion \(f(t)\) zu berechnen, ist es also gar nicht erforderlich, die Funktion \(f(t)\) explizit zu berechnen. Wir benötigen lediglich die partiellen Ableitungen der Funktion \(F(x,y)\).
Satz 8.55 (Ableitung von impliziten Funktionen) Es seien \(F(x,y)\) und \(f(t)\) Funktionen mit stetiger Ableitung. Wenn \(c(t)=F(t,f(t))\equiv \text{const}\), dann gilt \[ \begin{gathered} f'(t)=-\frac{F'_1(t,f(t))}{F'_2(t,f(t))}, \end{gathered} \] sofern der Nenner ungleich Null ist.
Sehen wir uns die Lösung der Musteraufgabe 8.54 nochmals an. Wir haben \[ \begin{gathered} F'_1(x,y)=2x+5y,\quad F'_2(x,y)=5x+2y. \end{gathered} \] Daraus folgt für \(x=t=3\) und \(y=f(t)=5\): \[ \begin{gathered} f'(3)=-\frac{F'_1(3,5)}{F'_2(3,5)}=-\frac{31}{25}=-1.24. \end{gathered} \] □
Musteraufgabe 8.56 Die Produktionsfunktion laute \(F(x,y)=100x^{0.1}y^{0.7}\). Im Moment verwendet der Hersteller die Faktorkombination \((x,y)=(2,1)\). Es soll nun der Einsatz von Faktor \(A\) erhöht und der Einsatz von Faktor \(B\) verringert werden, und zwar unter Beibehaltung des Produktionsniveaus. Zu berechnen ist Grenzrate der Substitution von Faktor \(A\) gegen Faktor \(B\).
Lösung: Wie berechnen die partiellen Ableitungen der Funktion \(F\): \[ \begin{gathered} F_1'(x,y)=10x^{-0.9}y^{0.7},\qquad F_2'(x,y)=70x^{0.1}y^{-0.3},\\[1ex] F_1'(2,1)=10\cdot 2^{-0.9},\qquad F_2'(2,1)=70\cdot 2^{0.1}. \end{gathered} \] Mit der Regel für die Ableitung impliziter Funktionen erhalten wir: \[ \begin{aligned} f'(2)&=-\frac{F_1'(2,1)}{F_2'(2,1)}=-\frac{10\cdot 2^{-0.9}}{70\cdot 2^{0.1}}=-\frac{10}{70\cdot 2}=-0.0714\\ &\implies \text{RTS} =0.0714\,. \end{aligned} \] □
8.8 Optimierung unter Nebenbedingungen
8.8.1 Einführung in die Aufgabenstellung
In Beispiel 8.51 haben wir schon auf einen wichtigen Punkt hingewiesen: Produktionsfaktoren haben Preise, daher ist es vernünftig zu fragen, wie ein bestimmter Output zu minimalen Kosten hergestellt werden kann.
Dieser Frage wollen wir nun nachgehen.
Ein Hersteller produziert ein Gut unter Verwendung von zwei Faktoren (z.B. Rohstoffen) \(A\) und \(B\). Die Kombination der Faktormengen \(x,\;y\) sei variabel. Die Produktionsfunktion des Herstellers laute \[ \begin{gathered} q=F(x,y). \end{gathered} \] Die Faktorkombination soll nun optimal gewählt werden, dh. dass die Produktionskosten minimiert werden sollen bei gegebenem Produktionsniveau.
Die Faktorpreise betragen \(a\) und \(b\) pro Mengeneinheit. Daher sind die Kosten (exkl. Fixkosten) der Faktorkombination \((x,y)\) und damit des Outputs \(q=F(x,y)\): \[ \begin{gathered} C(x,y)=ax+by. \end{gathered} \] Diese lineare Kostenfunktion soll minimiert werden unter der Nebenbedingung, dass der Output genau \(q=F(x,y)\) Einheiten betragen soll.
Man kann diese Aufgabe dadurch lösen, dass man die implizite Funktion \(f(t)\) bestimmt, die durch das Produktionsniveau \[ \begin{gathered} F(t,f(t))=q \end{gathered} \] definiert wird. Anschließend berechnet man die Kosten aller dieser Faktorkombinationen \[ \begin{gathered} c(t)=at+bf(t), \end{gathered} \] und bestimmt einen kritischen Punkt durch die Gleichung \[ \begin{gathered} c'(t)=a+bf'(t)=0\;. \end{gathered} \]
Musteraufgabe 8.58 Die Produktionsfunktion laute \(q=F(x,y)=100\,xy\) und Faktorpreise betragen 2 bzw. 3 GE pro Mengeneinheit. Man bestimme die optimale Faktorkombination beim Produktionsniveau \(q=200\).
Lösung: Die Funktion \(f(t)\) ist implizit definiert durch \(F(t,f(t))=200\), also \[ \begin{gathered} 100tf(t)=200 \;\implies\; f(t)=\frac{2}{t}\,. \end{gathered} \] Daher betragen die Kosten \[ \begin{gathered} c(t)=2t+3\cdot \frac{2}{t}=2t+\frac{6}{t}, \end{gathered} \] mit \(c'(t)=2-6/t^2\). Wir berechnen das Minimum durch \[ \begin{gathered} c'(t)=2-\frac{6}{t^2}=0\implies t=\pm\sqrt{3}. \end{gathered} \] Wir haben demnach ein Minimum in \(t=\sqrt{3}\). Die optimale Faktorkombination beträgt somit \(x=t=\sqrt{3}\simeq 1.73\) und \(y=f(t)=2/\sqrt{3}\simeq 1.15\). □
Bemerkung 8.59 Es ist uns in Musteraufgabe 8.58 nicht wirklich schwer gefallen die Lösung zu finden. Allerdings sollten wir uns keinen Illusionen hingeben. Einfach war es nur
Weil wir \(f(t)\) explizit berechnen konnten.
Damit reduzierten wir die Zielfunktion \(c(x,y)=2x+3y\) auf eine Funktion \(c(t)\) in bloß einer Variablen.
Wir haben die Nebenbedingung in die Zielfunktion eingearbeitet.
Falls das zu schwierig oder gar unmöglich ist, haben war aber eine elegante Alternative, die Methode von Lagrange
8.8.2 Die Methode von Lagrange
Es sei \(z=C(x,y)\) eine Zielfunktion, die unter der Nebenbedingung \(F(x,y)=q=\text{const}\) zu optimieren ist. Theoretisch würden wir mit \(x=t\) eine Funktion \(y=f(t)\) implizit durch die Gleichung \[ \begin{gathered} q=F(t,f(t)) \end{gathered} \] definieren und dann einen kritischen Punkt der Zielfunktion \[ \begin{gathered} c(t)=C(t,f(t)) \end{gathered} \] suchen. Dieser Lösungsweg kann wegen der Komplexität der expliziten Form von \(f(t)\) unbegehbar sein. Trotzdem kann man sich ansehen, welche Bedingungen ein kritischer Punkt erfüllen müsste.
Ein kritischer Punkt von \(c(t)\) muss die Gleichung \(c'(t)=0\), also auf Grund der Kettenregel (Satz 8.47) \[ \begin{gathered} C'_1(t,f(t))\cdot 1+C'_2(t,f(t))\,f'(t)=0\qquad \mbox{(A)} \end{gathered} \] erfüllen. Andererseits ist \(f'(t)\) die Ableitung einer implizit definierten Funktion und es gilt daher wegen Satz 8.55: \[ \begin{gathered} F'_1(t,f(t))\cdot 1+F'_2(t,f(t))\,f'(t)=0.\qquad \mbox{(B)} \end{gathered} \] Da \(f'(t)\) zwei lineare Gleichungen (A) und (B) (linear in der Unbekannten \(f'(t)\)) gleichzeitig erfüllt, müssen die Koeffizienten dieser Gleichungen proportional sein, dh. es gibt eine Zahl \(\lambda\), sodass \[ \begin{aligned} C'_1(t,f(t))&=\lambda F'_1(t,f(t))\\ C'_2(t,f(t))&=\lambda F'_2(t,f(t)). \end{aligned} \]
Satz 8.60 Es sei \(z=C(x,y)\) eine Zielfunktion, die unter der Nebenbedingung \(F(x,y)=q\) zu optimieren ist.
Ein Punkt \((x,y)\) ist genau dann ein kritischer Punkt dieses Optimierungsproblems, wenn es eine Zahl \(\lambda\) gibt, sodass \[ \begin{aligned} C'_1(x,y)&=\lambda F'_1(x,y), \end{aligned} \tag{8.5}\]
\[ \begin{aligned} C'_2(x,y)&=\lambda F'_2(x,y). \end{aligned} \tag{8.6}\] Die Zahl \(\lambda\) nennt man Lagrange-Multiplikator.
Diese Bedingung für kritische Punkte eines Optimierungsproblems mit einer Nebenbedingung vermeidet die explizite Darstellung der dahinter liegenden impliziten Funktion \(f(t)\).
Im Grunde könnte man es bei dieser Regel zum Aufsuchen von kritischen Punkte belassen und sie einfach anwenden. Es hat sich aber eingebürgert, ein Rechenschema zu verwenden, das unter dem Namen Methode der Lagrange-Multiplikatoren bekannt ist.
Bei diesem Rechenschema geht man so vor:
Schritt 1: Man definiert eine neue Zielfunktion \[ \begin{gathered} L(x,y,\lambda)=C(x,y)-\lambda(F(x,y)-q). \end{gathered} \] Das ist die sogenannte Lagrange-Funktion.
Schritt 2: Man sucht kritische Punkte der Lagrange-Funktion.
Ein kritischer Punkt der Lagrange-Funktion ist dadurch gekennzeichnet, dass alle (drei !) partiellen Ableitungen der Lagrange-Funktion (nach \(x\), nach \(y\) und nach \(\lambda\)) gleich Null sind: \[ \begin{aligned} L'_1&=C'_1-\lambda F'_1=0\\ L'_2&=C'_2-\lambda F'_2=0\\ L'_3&=-(F-q)=0\Leftrightarrow F-q=0. \end{aligned} \] Die beiden ersten Gleichungen sind genau die Bedingungen, die ein kritischer Punkt gemäß Satz 8.60 erfüllen muss. Die dritte Gleichung ist einfach die Nebenbedingung, unter der optimiert werden soll.
Sehen wir uns die Lösung der Musteraufgabe 8.58 nochmals an.
Die Lagrange-Funktion lautet \[ \begin{gathered} L(x,y,\lambda)=2x+3y-\lambda(100xy-200). \end{gathered} \] Wir bilden die partiellen Ableitungen nach \(x\) und \(y\) und setzen sie gleich Null: \[ \begin{aligned} L'_1&=2-100\lambda y=0\\ L'_2&=3-100\lambda x=0 \end{aligned} \] Die dritte Gleichung, die wir benötigen, ist die Nebenbedingung: \[ \begin{gathered} 100xy=200 \implies xy=2. \end{gathered} \] Wir lösen die ersten beiden Gleichungen nach \(x\) und \(y\) und drücken diese Lösungen als Funktionen von \(\lambda\) aus: \[ \begin{gathered} x=\frac{0.03}{\lambda},\quad y=\frac{0.02}{\lambda}.\qquad \mbox{(A)} \end{gathered} \] Nun setzen wir \(x\) und \(y\) in die Nebenbedingung, d.h. in \(xy=2\) ein: \[ \begin{gathered} \frac{0.0006}{\lambda^2}=2\implies \lambda=\pm\frac{\sqrt{3}}{100}. \end{gathered} \] Der Lagrange-Multiplikator kann also zwei Werte annehmen, daher haben wir nach Einsetzen in (A) auch zwei kritische Punkte: \[ \begin{gathered} \lambda_1=\frac{\sqrt{3}}{100},\quad x_1=\sqrt{3},\quad y_1=\frac{2}{\sqrt{3}}, \end{gathered} \] und \[ \begin{gathered} \lambda_2=-\frac{\sqrt{3}}{100},\quad x_2=-\sqrt{3},\quad y_2=-\frac{2}{\sqrt{3}}, \end{gathered} \] Nun stehen wir vor einem Problem: wir haben keine Bedingungen 2. Ordnung für das Lagrange-Problem formuliert, vergleichbar Satz 8.36 und Satz 8.41. Diese Bedingungen erlaubten uns, kritische Punkte als Maxima bzw. Minima zu klassifizieren.
Tatsächlich ist es möglich solche Bedingungen auch für den vorliegenden Fall anzugeben. Allerdings sind diese Bedingungen einfach zu kompliziert für uns, sodass wir uns irgendwie anders aus der Affäre ziehen müssen.
Der einfachste Weg scheint zu sein, für beide kritischen Punkte den Wert der Zielfunktion \(C(x,y)\) zu berechnen und jenen Punkt zu wählen, der den besseren Wert der Zielfunktion liefert. Besser bedeutet, bei einem Maximum den höheren, bei einem Minimum den niedrigeren Wert.
In unserem Beispiel ist \(C(x,y)=2x+3y\): \[ \begin{gathered} C\left(\sqrt{3},\frac{2}{\sqrt{3}}\right)=2\sqrt{3}+\frac{6}{\sqrt{3}}= 4\sqrt{3}=6.92820\\ C\left(-\sqrt{3},-\frac{2}{\sqrt{3}}\right)=-2\sqrt{3}-\frac{6}{\sqrt{3}}= -4\sqrt{3}=-6.92820 \end{gathered} \] Wir erkennen jedoch sofort, dass diese Vorgangsweise in unserem Beispiel nicht zielführend ist. Denn nach dieser Regel müssten wir als kritischen Punkt jenen zu \(\lambda_2=-\sqrt{3}/100\) nehmen, doch die dazugehörigen Werte von \(x\) und \(y\) sind beide negativ, also ökonomisch unplausibel, weil \(x\) und \(y\) Mengen sind, die nichtnegativ sein müssen.
In unserer Lage ist es daher besser mit ökonomischer Plausibilität zu argumentieren: wegen der Nichtnegativitäts-Forderung wählen wir die Lösung zu \(\lambda_1\), d.h. \(x=\sqrt{3}\simeq 1.73,y=2/\sqrt{3}\simeq 1.15\).
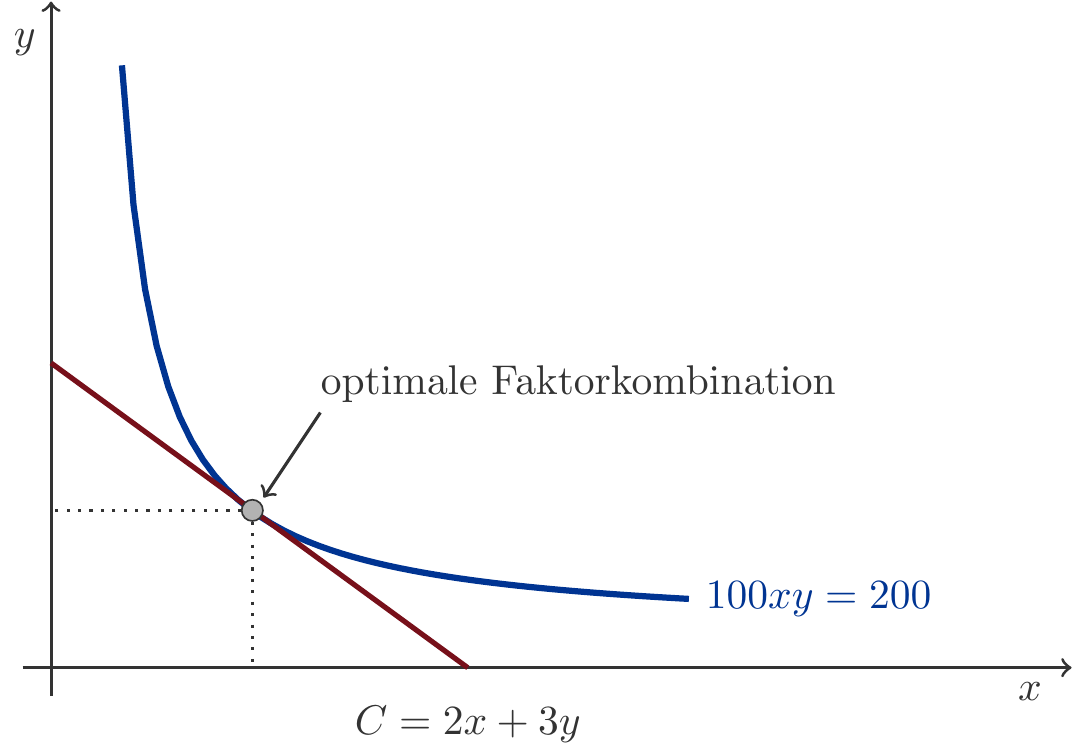
In Abbildung 8.13 ist die Lösung graphisch dargestellt. Eingezeichnet ist die Niveauline der Produktionsfunktion auf Höhe \(q=200\) und eine Niveauline der Kostenfunktion \(C(x,y)=2x+3y\), und zwar genau jene, welche die Niveauline der Produktionsfunktion berührt. Dieser Berührungspunkt ist das Optimum.
8.8.3 Ökonomische Interpretation des Lagrange-Multiplikators
Werfen wir nochmals einen Blick auf die Lagrange-Funktion: \[ \begin{gathered} L(x,y,\lambda)=C(x,y)-\lambda(F(x,y)-q), \end{gathered} \] doch diesmal gilt unser Interesse der Größe \(q\) in der Nebenbedingung. In ökonomischen Anwendungen repräsentiert \(q\) häufig eine Kapazitätsbeschränkung, d.h. eine Ressource ist nicht in beliebigem sondern in beschränktem Ausmaß \(q\) vorhanden. Im letzten Beispiel (Musteraufgabe 8.58) könnte etwa \(q=200\) die Maximalmenge sein, die aufgrund vorhandener technischer Ausstattung hergestellt werden kann.
Wenn wir nun den Wert von \(q\) ändern, dann wird sich auch die Lage des Optimums ändern. Mit anderen Worten: sowohl \(x\) als auch \(y\) sind Funktionen von \(q\) ! Angenommen, wir haben ein Optimum gefunden mit den Werten \(\lambda\), \(x^\ast\) und \(y^\ast\). Dann hängen diese Werte funktional von \(q\) ab und wir müssten schreiben: \[ \begin{gathered} \lambda=\lambda(q),\quad x^\ast=x^\ast(q),\quad y^\ast=y^\ast(q). \end{gathered} \] Das bedeutet aber auch, dass der Wert der Zielfunktion \(C(x,y)\) im Optimum von \(q\) abhängt: \[ \begin{gathered} C(x^\ast,y^\ast)=C^\ast(q). \end{gathered} \] Nun kann man etwas sehr Bemerkenswertes zeigen3: der Lagrange-Multiplikator ist nichts anderes als die Änderungsrate von \(C^\ast(q)\) bezüglich \(q\): \[ \begin{gathered} \frac{d C^\ast(q)}{dq}=\lambda(q), \end{gathered} \tag{8.7}\] \(\lambda(q)\) ist also die erste Ableitung von \(C^\ast(q)\) nach \(q\) und sagt uns, mit welcher Rate die Zielfunktion \(C^\ast(q)\) zunimmt oder abnimmt, wenn wir die Kapazitätsbeschränkung \(q\) lockern oder enger machen. Wenn wir \(q\) um einen kleinen Wert \(h\) ändern, so gilt näherungsweise wegen des Prinzips der lokalen Linearisierung (siehe 3.9): \[ \begin{gathered} C^\ast(q+h)-C^\ast(q)\approx \lambda(q)h.\qquad \mbox{(A)} \end{gathered} \] Tatsächlich hat der Multiplikator \(\lambda(q)\) den Charakter eines Preises, man spricht auch vom Schattenpreis einer beschränkten Ressource.
Kehren wir ein letztes Mal zu Musteraufgabe 8.58 zurück. Hier war \(q=200\) und wir fanden \[ \begin{gathered} \lambda(200)=\sqrt{3}/100=0.01732,\quad\text{mit } C^\ast(200)=4\sqrt{3}=6.92820\,. \end{gathered} \] Eine Erhöhung von \(q\) wird daher (weil \(\lambda>0\)) auch zu einer Erhöhung des Kostenminimums führen, aber diese wird recht gering ausfallen, denn \(\lambda\) hat einen niedrigen Wert. Um das zu sehen, wiederholen wir nun die Rechnung mit \(q=201\), wir erhöhen also das Outputniveau um eine ME, d.h. in (A) ist \(h=1\). Dann ergibt unsere Rechnung: \[ \begin{gathered} \lambda(201)=0.01728, \quad\text{mit } C^\ast(201)=6.94550\,. \end{gathered} \] Und wirklich ist \[ \begin{gathered} C^\ast(201)-C^\ast(200)=0.0173\simeq \lambda(200). \end{gathered} \]
Wir schließen dieses Kapitel mit einem weiteren Beispiel ab.
Musteraufgabe 8.61 Die Produktionsfunktion eines Herstellers laute \(F(x,y)=x^2+5xy+y^2\). Man bestimme die optimale Faktorkombination zu den Faktorpreisen 15 und 20 und dem Produktionsniveau 2500.
Lösung: Die Lagrange-Funktion lautet \[ \begin{gathered} L(x,y,\lambda)=15x+20y-\lambda(x^2+5xy+y^2-2500). \end{gathered} \] Wir bilden die partiellen Ableitungen und setzen sie gleich Null: \[ \begin{aligned} L'_1&=15-\lambda(2x+5y)=0\\ L'_2&=20-\lambda(5x+2y)=0 \end{aligned} \] Als dritte Gleichung haben wir die Nebenbedingung: \[ \begin{gathered} x^2+5xy+y^2=2500. \end{gathered} \] Die ersten beiden Gleichungen bilden ein lineares Gleichungssystem \[ \begin{gathered} 2x+5y=\frac{15}{\lambda},\qquad 5x+2y=\frac{20}{\lambda}. \end{gathered} \] Wir lösen dieses Gleichungssystem und drücken die Lösungen \(x\) und \(y\) als Funktionen von \(\lambda\) aus: \[ \begin{gathered} x=\frac{10}{3\lambda},\quad y=\frac{5}{3\lambda}\,.\qquad \mbox{(A)} \end{gathered} \] Das setzen wir in die Nebenbedingung ein: \[ \begin{gathered} \frac{100}{9\lambda^2}+\frac{250}{9\lambda^2}+\frac{25}{9\lambda^2}=2500\implies \lambda^2=\frac{375}{22500} \implies\lambda=\pm 0.1291\,. \end{gathered} \] Wieder hat der Lagrange-Multiplikator zwei mögliche Werte, allerdings ist nur der positive Wert \(\lambda=0.1291\) von Interesse, denn nur er garantiert positive Lösungen4. Durch Einsetzen in (A) erhalten wir das Kostenminimum bei: \[ \begin{gathered} x=\frac{10}{3\cdot 0.1291}=25.82,\quad y=\frac{5}{3\cdot 0.1291}=12.91 \end{gathered} \] Siehe Abbildung 8.14 für eine Illustration.
8.9 Weitere Übungsaufgaben
-
Bestimmen Sie die ersten partiellen Ableitungen von \(f(x,y)=\sqrt{x/y}\) an der Stelle \({\mathbf a}^\top =(2,5)\).
Lösung: \(\displaystyle f_1'(x,y)=\frac{1}{2\sqrt{xy}}, \;f_2'(x,y)=-\frac{\sqrt{x}}{2y\sqrt{y}}\),
\(f_1'(2,5)=0.1581,\;f_2'(2,5)=-0.0623\) -
Bestimmen Sie die ersten partiellen Ableitungen von \(f(x,y)=e^{x^2+xy+y^2}\) an der Stelle \({\mathbf a}^\top =(0,1)\).
Lösung: \(\displaystyle f_1'(x,y)=(2x+y)e^{x^2+xy+y^2},\;f_2'(x,y)=(x+2y)e^{x²+xy+y²}\),
\(f_1'(0,1)=2.7183,\;f_2'(0,1)=5.4366\) -
Bestimmen Sie die ersten partiellen Ableitungen von \(f(x,y)=x^y\) an der Stelle \({\mathbf a}^\top =(1,0)\).
Lösung: \(f_1'(x,y)=y\,x^{y-1},\;f_2'(x,y)=x^y\ln x\),
\(f_1'(1,0)=0,\;f_2'(1,0)=0\). -
Bestimmen Sie die ersten partiellen Ableitungen von \(f(x,y)=x^2\ln(xy)\) an der Stelle \({\mathbf a}^\top =(2,2)\).
Lösung: \(\displaystyle f_1'(x,y)=2x\ln(xy)+x,\;f_2'(x,y)=x^2/y\),
\(f_1'(2,2)=7.5452,\;f_2'(2,2)=2\) -
Bestimmen Sie die Richtungsableitung von \(f(x,y)=e^{x-y}\) entlang der gleichförmigen Bewegung \(\mathbf x=\mathbf a+t\mathbf v\) mit \({\mathbf a}^\top =(0,0)\) und \({\mathbf v}^\top =(1,1)\) in \(t=0\).
Lösung: \(0\)
-
Bestimmen Sie die Richtungsableitung von \(f(x,y)=x^2-5y\) entlang der gleichförmigen Bewegung \(\mathbf x=\mathbf a+t\mathbf v\) mit \({\mathbf a}^\top =(1,0)\) und \({\mathbf v}^\top =(-1,2)\) in \(t=0\).
Lösung: \(-12\)
-
Welchen Wert hat die Hesse-Matrix der Funktion \(f(x,y)=e^{x^2+2y}\) im Punkt \((0,0)\)?
Lösung: \(\displaystyle \boldsymbol{f}''(x,y)=e^{x^2+2y}\left(\begin{array}{cc}2+4x^2 & 4x\\4x & 4\end{array}\right),\; \boldsymbol{f}''(0,0)=\left( \begin{array}{cc}2 & 0\\0 & 4\end{array}\right)\).
-
Welchen Wert hat die Hesse-Matrix der Funktion \(f(x,y)=\sqrt{xy}\) im Punkt \((1,1)\)?
Lösung: \(\displaystyle \boldsymbol{f}''(x,y)=\left(\begin{array}{cc}-\frac{\sqrt{y}}{4x\sqrt{x}} & \frac{1}{4\sqrt{xy}}\\\frac{1}{4\sqrt{xy}} & -\frac{\sqrt{x}}{4y\sqrt{y}} \end{array}\right)\),
\(\displaystyle \boldsymbol{f}''(1,1)=\frac{1}{4}\left( \begin{array}{rr}-1 & 1\\1 & -1\end{array}\right)\). -
Welchen Wert hat die Hesse-Matrix der Funktion \[ \begin{gathered} f(x,y)=-2x^{2} y^{3}+5x^{2} y^{2}+5x y^{2}+4x y+2 \end{gathered} \] im Punkt \((-1,1)\)?
Lösung: \(\displaystyle\boldsymbol{f}''(1,1)=6\left( \begin{array}{rr}1 & 1\\1 & -2\end{array}\right)\).
-
Es sei \(\displaystyle q(p_1,p_2)=\frac{10}{p_1p_2}\) die Nachfragefunktion nach einem Gut \(Q\) in Abhängigkeit von dessen Preis \(p_1\) und dem Preis \(p_2\) eines Konkurrenzprodukts. Berechnen Sie die partiellen Preiselastizitäten bez. \(p_1\) und \(p_2\).
Lösung: \(\epsilon_1(p_1,p_2)=\epsilon_2(p_1,p_2)=-1\)
-
Finden Sie die globalen Extremwerte der Funktion \[ \begin{gathered} f(x,y) = 7x^{2} +10x y-102x +9 y^{2}-138 y+9. \end{gathered} \]
Lösung: Minimum in \((3,6)\).
-
Finden Sie die globalen Extremwerte der Funktion \[ \begin{gathered} f(x,y) = -10x^{2} -6x y-32x -6 y^{2}+72 y+8. \end{gathered} \]
Lösung: Maximum in \((-4,8)\).
-
Ein Monopolunternehmen bietet zwei Güter zu Preisen \(p_1\) und \(p_2\) an. Die Nachfrage wird durch die Nachfragefunktionen \[ \begin{aligned} q_1&=D_1(p_1,p_2)=400-2p_1+p_2\\ q_2&=D_2(p_1,p_2)=280+p_1-5p_2 \end{aligned} \] bestimmt. Die Herstellungskosten (exkl. Fixkosten) der Güter betragen 14 bzw. 20 GE. Bei welchen Preisen entsteht der größte Gewinn?
Lösung: \(p_1=401/3,\,p_2=190/3\).
-
Ein Monopolunternehmen bietet zwei Güter zu Preisen \(p_1\) und \(p_2\) an. Die Nachfrage wird durch die Nachfragefunktionen \[ \begin{aligned} q_1&=D_1(p_1,p_2)=850-p_1-p_2\\ q_2&=D_2(p_1,p_2)=780-p_1-3p_2 \end{aligned} \] bestimmt. Die Herstellungskosten (exkl. Fixkosten) der Güter betragen 28 bzw. 44 GE. Bei welchen Preisen entsteht der größte Gewinn?
Lösung: \(p_1=456.5,\,p_2=4.5\).
-
Es sei \(f(x,y)=3x e^{-2y}\) und \(\mathbf x=\mathbf g(t)\) mit \(g_1(t)=-8 t^2\) und \(g_2(t)=2\ln t\). Bestimmen Sie \(c'(1.2)\) für \(c(t)=f(\mathbf g(t))\).
Lösung: \(c'(1.2)=27.78\)
-
Die Produktionsfunktion eines Unternehmens laute \[ \begin{gathered} F(x,y)=3x^{2} +2x y+3 y^{2}, \end{gathered} \] wobei \(x\) und \(y\) die eingesetzten Mengen der beiden Produktionsfaktoren \(A\) und \(B\) bezeichnen. Im Moment verwendet der Hersteller die Faktorkombination \((x,y)= (7,5)\). Es soll nun der Einsatz von Faktor \(A\) erhöht und der Einsatz von \(B\) verringert werden, und zwar unter Beibehaltung des Produktionsniveaus. Berechnen Sie die Grenzrate der Substitution von Faktor \(A\) gegen Faktor \(B\).
Lösung: \(1.18\)
-
Finden Sie das Maximum der Funktion \(F(x,y)=xy\) unter der Nebenbedingung \(5x+2y=20\).
Lösung: \(x=2, y=5\).
-
Finden Sie das Minimum der Funktion \(F(x,y)=x^2+y^2\) unter der Nebenbedingung \(2x+3y=26\).
Lösung: \(x=4, y=6\).
-
Die Produktionsfunktion eines Unternehmens laute \[ \begin{gathered} F(x,y)=2x^{2} +14x y+4 y^{2}, \end{gathered} \] wobei \(x\) und \(y\) die eingesetzten Mengen der beiden Produktionsfaktoren \(A\) und \(B\) bezeichnen. Die Preise der Produktionsfaktoren betragen pro Mengeneinheit 15 bzw. 19 GE. Berechnen Sie die eingesetzten Mengen an Produktionsfaktoren, wenn vom Endprodukt 6400 Mengeneinheiten zu minimalen Kosten gefertigt werden.
Lösung: \(x=18.74,\,y=17.20\).
-
Die Produktionsfunktion eines Unternehmens laute \[ \begin{gathered} F(x,y)=173 x^{0.65} y^{0.43}, \end{gathered} \] wobei \(x\) und \(y\) die eingesetzten Mengen der beiden Produktionsfaktoren \(A\) und \(B\) bezeichnen. Die Preise der Produktionsfaktoren betragen pro Mengeneinheit 20 bzw. 10 GE. Berechnen Sie die eingesetzten Menge an Produktionsfaktoren, wenn vom Endprodukt 9500 Mengeneinheiten zu minimalen Kosten gefertigt werden.
Lösung: \(x=36.51,\,y=48.30\).
Leserinnen und Leser, die mit dem Gebrauch von Winkelfunktionen nicht vertraut sind, müssen sich keine Sorgen machen, diese Funktionen werden auch in diesem Kapitel keine Rolle spielen.↩︎
Dieses Werkzeug wird uns noch des öfteren gute Dienste leisten.↩︎
Es ist etwas tricky, das zu zeigen!↩︎
\(x\) und \(y\) sind Mengen und daher nichtnegativ.↩︎