5  Wahrscheinlichkeitsrechnung

5.1 Grundbegriffe

5.1.1 Zufallsexperimente und Ergebnismenge

An den Beginn unserer Überlegungen stellen wir den Begriff des Experiments. Darunter verstehen wir einen Vorgang, der unter genau definierten Bedingungen abläuft und ein Ergebnis produziert, das beobachten werden kann.

Jedes Experiment, das wenigstens zwei mögliche Resultate hat, nennen wir ein Zufallsexperiment. Oder anders ausgedrückt: jedes Experiment, das, unter gleichbleibenden Bedingungen wiederholt, immer das gleiche Ergebnis liefert, ist kein Zufallsexperiment.

Das Wesen des Zufallsexperiments ist die prinzipielle Nichtvorhersagbarkeit des Ergebnisses. Allerdings stellt sich damit sofort die Frage: wie soll man eine mathematische Theorie entwickeln für Vorgänge, die eben diese Eigenschaft der Nichtvorhersagbarkeit haben?

Die Antwort liegt in der Wiederholung. Wenn ein Zufallsexperiment oftmals wiederholt wird, dann zeigen sich nach und nach gewisse Regelmäßigkeiten, die sich schließlich zu Gesetzmäßigkeiten verdichten, Gesetzmäßigkeiten, die nicht nur von außerordentlicher Schönheit und Ästhetik sind, sondern auch Vorhersagen von atemberaubender Genauigkeit erlauben.

Um ein Zufallsexperiment mathematisch zu beschreiben, benötigen wir einige Grundbegriffe. Wir beginnen mit:

Definition 5.1 (Ergebnismenge) Die Ergebnismenge \(\Omega\) eines Experiments ist die Menge aller möglichen Resultate, die ein Experiment haben kann.

Ein weiterer Grundbegriff ist der des Ereignisses.

5.1.2 Ereignisse

Definition 5.2 (Ereignis) Unter einem Ereignis versteht man eine Aussage über ein mögliches Ergebnis eines Zufallsexperiments. Jedes Ereignis entspricht daher einer Teilmenge der Ergebnismenge, nämlich jener Teilmenge von Ergebnissen, für die die Aussage zutrifft.

Es ist üblich Ereignisse durch lateinische Großbuchstaben zu bezeichnen, vorzugsweise aus der ersten Hälfte des Alphabets, z.B. \(A\), \(B\) usw.

Um den Begriff des Ereignisses besser zu verstehen, sehen wir uns Beispiel an.

Musteraufgabe 5.3 Ein Zufallsexperiment bestehe darin, einen regelmäßigen sechseitigen Würfel, dessen Seiten mit den Zahlen \(1,2,\ldots,6\) versehen sind, genau einmal zu werfen. Stellen Sie das Ereignis {ich würfle eine gerade Augenzahl} durch eine Teilmenge der Ergebnismenge \(\Omega\) dar.

Lösung: Die Ergebnismenge ist \(\Omega=\{1,2,\ldots,6\}\). Das Ereignis {gerade Augenzahl} entspricht der Teilmenge \(A=\{2,4,6\}\). Wenn man eine Augenzahl (z.B. die Augenzahl 2) würfelt, die in der Teilmenge \(A\) enthalten ist, dann hat das Ereignis \(A\) stattgefunden (ist eingetreten). □

In dieser Aufgabe war die Ergebnismenge von vergleichsweise sehr geringer Größe, sodass wir \(\Omega\) problemlos als Liste anschreiben konnten.

Sehr häufig jedoch enthält die Ergebnismenge enorm viele Elemente, sodass es nicht mehr sinnvoll oder gar möglich ist \(\Omega\) als Liste anzugeben. Das ist aber auch in der Regel nicht notwendig, denn meist interessiert uns nur die Größe oder Mächtigkeit dieser Menge, die wir mit \(|\Omega|\) bezeichnen.

Musteraufgabe 5.4 Bei einer Lotterie werden Lose mit den Nummern \(1,2,\ldots,45\) zur Ziehung angeboten. Die Ziehung bestehe darin, dass eine Stichprobe von \(6\) Losen (nacheinander und ohne Zurücklegen) gezogen wird. Bestimmen Sie den Umfang der Ergebnismenge und jener Teilmenge, die dem Ereignis {Haupttreffer} entspricht.

Lösung: Die Ergebnismenge \(\Omega\) ist die Menge aller Listen (geordneter Mengen) der Länge sechs, die sich aus den Zahlen \(1,2,\ldots,45\) bilden lassen.

Wieviele Elemente enthält \(\Omega\)? Das ist einfach: für die erste Ziehung haben wir 45 Möglichkeiten, für die zweite nur mehr 44, denn es wird ohne Zurücklegen gezogen. Für jede weitere Ziehung vermindert sich daher die Anzahl der Möglichkeiten um eins. Insgesamt haben wir somit: \[ \begin{gathered} |\Omega|=45\cdot 44\cdot 43\cdot 42 \cdot 41 \cdot 40=5\,864\,443\,200 \end{gathered} \] Möglichkeiten. Bei dieser Lotterie besteht ein Tipp darin, eine Menge von 6 Zahlen anzugeben. Dieser Tipp ist dann der Haupttreffer, wenn die Zahlen des Tipps, abgesehen von der Reihenfolge, mit dem Ziehungsergebnis übereinstimmen. Das Ereignis \(A=\{\mathit{Haupttreffer}\}\) entspricht daher der Teilmenge \(A\subseteq\Omega\), die aus allen Permutationen der gezogenen Tippreihe besteht. Diese Teilmenge \(A\) enthält \[ \begin{gathered} |A|=6\cdot 5\cdot 4\cdot 3\cdot 2\cdot 1=6! = 720 \end{gathered} \] Elemente. Wir sehen, dass \(A\) im Vergleich zu \(\Omega\) eine sehr kleine Menge ist und erwarten daher, dass das Ereignis \(A\) im Experiment eher selten zu beobachten sein wird. □

Zufallsgrößen

In vielen Fällen werden Ereignisse durch Zufallsgrößen definiert. Eine Zufallsgröße \(X\) ist eine im Zuge des Zufallsexperiments beobachtbare zufällige Zahl. Mathematisch gesehen ist eine Zufallsgröße \(X\) eine Funktion (Zuordungsvorschrift), die jedem möglichen Ergebnis \(\omega\in\Omega\) des Zufallsexperiments eine Zahl \(X(\omega)\) zuweist. Jede Aussage über die Zufallsgröße stellt ein Ereignis dar. Der große Vorteil von Zufallsgrößen ist, dass wir mit ihnen rechnen können. Wir können sie addieren, multiplizieren, usw.

Musteraufgabe 5.5 Ein Würfel mit den Augenzahlen \(1,2,\ldots,6\) wird zweimal geworfen. Es sei \(X\) die Augenzahl des ersten Wurfs, \(Y\) jene des zweiten Wurfs. Bestimmen Sie jene Teilmenge der Ergebnismenge, die dem Ereignis \(\{X+Y<4\}\) entspricht.

Lösung: In diesem Experiment besteht die Ergebnismenge \(\Omega\) aus allen Paaren \((a,b)\), die wir aus den Zahlen \(1,2,\ldots,6\) bilden können: \[ \begin{gathered} \Omega=\{(1,1),(1,2),\ldots,(6,6)\},\quad |\Omega|=36. \end{gathered} \] Dann ist \[ \begin{gathered} \{X+Y<4\}=\{(1,1),(1,2),(2,1)\},\quad|\{X+Y<4\}|=3. \end{gathered} \] □

5.1.3 Verknüpfung von Ereignissen

Wir haben bereits festgehalten: Ereignisse sind Teilmengen der Ergebnismenge \(\Omega\). Da jede Menge die leere Menge \(\varnothing\) und sich selbst als Teilmenge enthält, also \(\varnothing\subset \Omega\) und \(\Omega\subset \Omega\), sind auch \(\varnothing\) und \(\Omega\) Ereignisse, allerdings von besonderer Art:

• \(\varnothing\) ist das unmögliche Ereignis, denn das Experiment muss notwendigerweise ein Ergebnis haben, das in \(\Omega\) liegt.

• \(\Omega\) ist das sichere Ereignis, denn \(\Omega\) enthält eben alle möglichen Ergebnisse.

Bekanntlich können durch einfache Mengenoperationen aus Teilmengen von \(\Omega\) neue Mengen gebildet werden, die selber wiederum Ereignisse sind.

Abbildung 5.1: Verknüpfungen von Ereignissen.

Die wichtigsten Mengenoperationen und ihre Interpretation sind (siehe Abbildung 5.1):

• \(A\cup B\) – die Vereinigung zweier Mengen
  Das ist die Menge aller Elemente, die zu \(A\) oder \(B\) gehören. Interpretiert als zufälliges Ereignis: Ereignis \(A\) oder \(B\) tritt ein.

• \(A\cap B\) – der Durchschnitt zweier Mengen
  Das ist die Menge aller Elemente, die zu \(A\) und \(B\) gehören. Interpretiert als zufälliges Ereignis: Ereignis \(A\) und \(B\) treten ein.

• \(A'\) – das Komplement einer Menge
  Das ist die Menge aller Elemente, die nicht zu \(A\) gehören. Als zufälliges Ereignis interpretieren wir das Komplement als: das Ereignis \(A\) tritt nicht ein.

Ein wichtiger Sonderfall liegt vor, wenn \(A\cap B=\varnothing\). In diesem Fall sagen wir, die beiden Ereignisse \(A\) und \(B\) sind unvereinbar, sie schließen einander aus. Kurz, \(A\cap B\) kann nicht eintreten.

Es sei beispielsweise das Experiment das einmalige Werfen eines Würfel und \[ \begin{gathered} A=\{\text{gerade Zahl}\}=\{2,4,6\},\quad B=\{\text{ungerade Zahl}\}=\{1,3,5\}. \end{gathered} \] Dann ist \(A\cap B=\varnothing\), es ist eben nicht möglich bei einmaligen Werfen eines Würfel eine Zahl zu erhalten, das gleichzeitig gerade und ungerade ist.

Beispiel 5.6 (Glücksspiel)

Bei einem Glücksspiel wird eine Serie von \(n\) Einzelspielen durchgeführt, von denen jedes einzelne die möglichen Ergebnisse Gewinn (\(G\)) und Verlust (\(V\)) hat. Die Ergebnismenge \(\Omega\) der Spielserie besteht daher aus allen Listen der Länge \(n\), die man aus den beiden Buchstaben \(G\) und \(V\) bilden kann. Sie enthält \(|\Omega|=2^n\) Listen.

Das ist leicht zu verstehen: jede Liste hat \(n\) Plätze, für jeden Platz haben wir zwei Möglichkeiten, ihn zu besetzen, nämlich \(G\) oder \(V\). Daher ist die Anzahl der verschiedenen Listen \(2^n\).

Es sei nun \(S_n\) die Häufigkeit (Anzahl), mit der der Buchstabe \(G\) im Ergebnis \(\omega\in \Omega\) auftritt. Dann ist \(S_n\) eine Zufallsgröße mit den möglichen Werten \(0,1,\ldots,n\). Diese Zufallsgröße gibt uns die Anzahl der Gewinne in der Spielserie an.

Das Ereignis {mindestens \(k\) Gewinne} kann man symbolisch durch \(\{S_n\ge k\}\) bezeichnen. Es entspricht der Menge all jener Listen \(\omega\in \Omega\), die mindestens \(k\)-mal den Buchstaben \(G\) enthalten.

Musteraufgabe 5.7 Bei einem Glücksspiel wird eine Serie von \(5\) Einzelspielen durchgeführt, von denen jedes einzelne die möglichen Ergebnisse {Gewinn} (\(G\)) und {Verlust} (\(V\)) hat. Wie hoch ist der Anteil (Prozentsatz) jener Serien, bei denen genau ein Gewinn auftritt?

Lösung: \(\Omega\) ist die Menge aller 5er-Listen, die wir aus den Buchstaben \(G\) und \(V\) bilden können, deshalb ist \(|\Omega|=2^5=32\). Es sei \(A=\{\mathit{genau~ein~Gewinn}\}\).

Dann ist \(|A|=5\), denn nur diese 5 Listen in \(\Omega\) enthalten genau einen Buchstaben \(G\): \[ \begin{gathered} \mathit{GVVVV},\quad\mathit{VGVVV},\quad \mathit{VVGVV},\quad \mathit{VVVGV}, \quad\mathit{VVVVG}. \end{gathered} \] Daher beträgt der Anteil \(5/2^5=0.15625\), also 15.625 %. □

Der eben berechnete Prozentsatz ist unser erstes Beispiel für eine Wahrscheinlichkeit.

5.1.4 Wahrscheinlichkeiten

Es liege ein Zufallsexperiment mit der Ergebnismenge \(\Omega\) vor. Man sagt, dass ein Ereignis \(A\) eingetreten ist, wenn nach der Durchführung des Zufallsexperiments das realisierte Ergebnis \(\omega\) in der Teilmenge \(A\subseteq\Omega\) enthalten ist. Dies bedeutet ja nichts anderes, als dass die dem Ereignis \(A\) entsprechende Aussage über das Ergebnis zutreffend ist.

Bevor ein Zufallsexperiment durchgeführt wird, ist grundsätzlich nicht vorhersehbar, ob ein bestimmtes Ereignis eintritt oder nicht. Trotzdem ist es in der Regel so, dass nach zahlreichen Wiederholungen des Zufallsexperiments manche Ereignisse häufiger eingetreten sind als andere. Daher liegt es nahe, die statistische Häufigkeit des Auftretens von Ereignissen als Ausgangspunkt für die Konstruktion des Begriffs der Wahrscheinlichkeit eines Ereignisses zu verwenden.

Definition 5.8 Es sei \(f_n(A)\) die relative Häufigkeit, mit der das Ereignis \(A\) bei einer Serie von \(n\) Wiederholungen des Zufallsexperiments auftritt. Man geht nun von der Vorstellung aus, dass sich diese relative Häufigkeit mit wachsender Anzahl von Wiederholungen einem festen Prozentsatz annähert: \[ \begin{gathered} \lim_{n\to\infty} f_n(A)=:P(A). \end{gathered} \tag{5.1}\] Diesen Grenzwert \(P(A)\) der relativen Häufigkeiten nennt man die Wahrscheinlichkeit von \(A\).

Diese eben beschriebene intuitive Erklärung des Wahrscheinlichkeitsbegriffs ist keine Definition im mathematischen Sinn. Sie ist lediglich eine Annahme, die es ermöglichen soll, den theoretischen Begriff der Wahrscheinlichkeit empirisch fassbar zu machen. Man könnte diese Annahme als empirisches Gesetz der großen Zahlen bezeichnen. Die Brauchbarkeit dieser Annahme hat sich durch den Umstand erwiesen, dass die darauf aufbauende mathematische Wahrscheinlichkeitstheorie (Stochastik) gültige Aussagen über reale Anwendungen machen kann.

Abbildung 5.2: Relative Häufigkeit für Zahl aus 200 Münzwürfen.

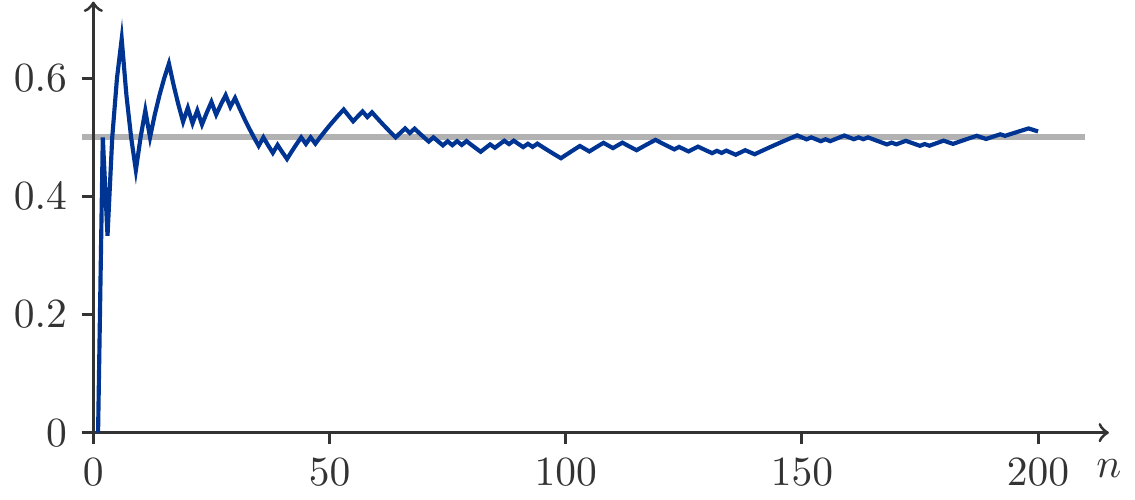
Für Abbildung 5.2 wurden 200 Münzwürfen simuliert. Wir sehen, wie sich die relative Häufigkeit \(f_n(A)\) des Ereignisses \(A=\{\mathit{Zahl}\}\) dem Wert \(1/2\) annähert.

Aus der intuitiven Erklärung des Wahrscheinlichkeitsbegriffs leiten sich die grundlegenden Eigenschaften von Wahrscheinlichkeiten ab:

Satz 5.9 (Eigenschaften von Wahrscheinlichkeiten) Es sei \(\Omega\) die Ergebnismenge eines Zufallsexperiments und \(A\), \(B\), \(C\),…seien beobachtbare Ereignisse. Dann gelten für die Wahrscheinlichkeiten der Ereignisse folgende Gesetze:

1. \(0\le P(A) \le 1\).

2. \(P(\Omega)=1\): Das sichere Ereignis hat die Wahrscheinlichkeit 1.

3. \(P(\varnothing)=0\): Das unmögliche Ereignis hat die Wahrscheinlichkeit 0.

4. Wenn \(A\cap B=\varnothing\), die Ereignisse \(A\) und \(B\) also unvereinbar sind, dann gilt das Additionsgesetz: \[ \begin{gathered} P(A\cup B)=P(A)+P(B). \end{gathered} \tag{5.2}\]

Das Additionsgesetz ist die wichtigste Rechenregel für Wahrscheinlichkeiten.

Die numerische Bestimmung von Wahrscheinlichkeiten mit Hilfe des Gesetzes der großen Zahlen (Definition 5.8) ist sehr oft mit großem Aufwand verbunden. Allerdings gibt es Situationen, in denen wir leichter zum Ziel kommen. Dazu müssen freilich zwei Voraussetzungen erfüllt sein.

Definition 5.10 (Klassischer Wahrscheinlichkeitsbegriff) Wenn

• \(\Omega\) eine endliche Menge ist, und

• alle Ergebnisse des Experiments gleich wahrscheinlich sind,

dann gilt für alle Ereignisse \(A\subset \Omega\): \[ \begin{gathered} P(A)=\frac{|A|}{|\Omega|}=\frac{\text{Zahl der günstigen Fälle}}{\text{Zahl der möglichen Fälle}}\,. \end{gathered} \tag{5.3}\]

Man kann zeigen, dass der klassische Wahrscheinlichkeitsbegriff alle im Satz 5.9 geforderten Eigenschaften besitzt. Allerdings, ob die Voraussetzungen von Definition 5.10 erfüllt sind, muss im Einzelfall überprüft werden. Insbesondere die Hypothese der Gleichwahrscheinlichkeit ist oft kritisch zu sehen. Die Statistik stellt jedoch Methoden zur Verfügung, die eine Überprüfung dieser Hypothese erlauben.

Wenn alle Voraussetzungen erfüllt sind, dann ist die Bestimmung von Wahrscheinlichkeiten mit Definition 5.10 im Prinzip einfach. Wir müssen nur die Größen (Mächtigkeiten) der Ergebnismenge \(\Omega\) und der uns interessierenden Ereignisse \(A\), \(B\), usw. durch Abzählen ermitteln.

Musteraufgabe 5.11 Ein Würfel wird einmal geworfen. Wie groß die Wahrscheinlichkeit dafür, dass eine gerade Augenzahl geworfen wird.

Lösung: Wir haben bereits festgestellt: \[ \begin{gathered} \Omega=\{1,2,3,4,5,6\},\quad |\Omega|=6;\qquad A=\{2,4,6\},\quad |A|=3. \end{gathered} \] Aus (5.3) folgt daher: \[ \begin{gathered} P(A)=\frac{|A|}{|\Omega|}=\frac{3}{6}=\frac{1}{2}. \end{gathered} \] Dieses Ergebnis gilt unter der Voraussetzung, dass der Würfel fair, die Hypothese der Gleichwahrscheinlichkeit also erfüllt ist.

Wir könnten auch experimentell an das Problem herangehen und das empirische Gesetz der großen Zahlen (5.1) bemühen. Dazu wäre es notwendig, den Würfel sehr oft, vielleicht einige tausend Male, zu werfen und abzuzählen, wie oft eine gerade Zahl erscheint. Die relative Häufigkeit dafür sollte mit wachsender Versuchszahl nahe bei \(0.5\) liegen. Wir erwarten ein Bild ganz ähnlich der Abbildung 5.2. □

Musteraufgabe 5.12 Wie groß ist die Wahrscheinlichkeit für einen Haupttreffer bei der Lotterie 6 aus 45?

Lösung: In der Lösung von Musteraufgabe 5.4 haben wir bereits gefunden: \[ \begin{aligned} |\Omega| & =45\cdot 44\cdot 43\cdot 42\cdot 41\cdot 40=5\,864\,443\,200,\\ |A| & =6!=720,\\ \implies P(A) =\frac{|A|}{|\Omega|} & =\frac{720}{5864443200} =0.0000001227738\,. \end{aligned} \] □

Die Interpretation der Wahrscheinlichkeit als langfristig zu erwartender Anteil von Realisationen ermöglicht eine Schätzung der Anzahl von Realisationen in einer großen Serie von Versuchswiederholungen.

Musteraufgabe 5.13 In Österreich schätzt man den Anteil der Schadensfälle, die in betrügerischer Absicht oder manipuliert an Versicherungsunternehmen gemeldet werden, auf 8.5% quer über alle Sparten. Mit wievielen Betrugsfällen pro Jahr muss eine Versicherung rechnen, wenn sie im Jahr 150 000 Schadensfälle abzuwickeln hat?

Lösung: Es sei \(N=150000\) die Anzahl der Versicherungsfälle pro Jahr und \(p=0.085\) der prozentuelle Anteil der betrügerischen Schadensmeldungen. Die erwartete Häufigkeit von Betrugsfällen pro Jahr beträgt \[ \begin{gathered} Np=150\,000\cdot 0.085= 12750. \end{gathered} \] □

Musteraufgabe 5.14 Eine Firma verlost unter ihren 8000 Kunden eine Urlaubsreise mit Hilfe eines Rubbelspiels. Bei diesem Rubbelspiel müssen unter 10 Rubbelfeldern genau die drei Richtigen aufgerubbelt werden. Mit wievielen Gewinnern der Urlaubsreise muss die Firma rechnen?

Lösung: Wir nehmen an, dass die Teilnehmer die Rubbelfelder rein zufällig aufrubbeln. Das bedeutet, dass alle \(10\cdot 9\cdot 8=720\) Möglichkeiten, drei Felder hintereinander aufzurubbeln, die gleiche Wahrscheinlichkeit \(1/720\) haben. Es gibt \(3\cdot 2\cdot 1=6\) Möglichkeiten, die drei richtigen Felder in unterschiedlicher Reihenfolge zu treffen. Daher hat beim Aufrubbeln einer Rubbelkarte das Ereignis \(A=\{\mathit{Gewinn~der~Urlaubsreise}\}\) die Wahrscheinlichkeit \[ \begin{gathered} P(A)=\frac{6}{720}=0.00833. \end{gathered} \] Bei \(N=8000\) Teilnehmern ist daher mit \(N\cdot P(A)= 8000\cdot 0.00833=66.67\approx 67\) Gewinnern zu rechnen. □

5.1.5 Eine Verallgemeinerung des Additionsgesetzes

Das Additionsgesetz (5.2) erlaubt uns die Wahrscheinlichkeit für das Eintreten von \(A\) oder \(B\) zu berechnen, falls die Ereignisse \(A\) und \(B\) unvereinbar sind, also \(A\cap B=\varnothing\). Wenn \(A\) und \(B\) jedoch nicht unvereinbar sind, dann gilt eine allgemeinere Formel: \[ \begin{gathered} P(A\cup B)=P(A)+P(B)-P(A\cap B). \end{gathered} \tag{5.4}\] Eine intuitive Erklärung gewährt uns ein Blick auf Abbildung 5.3.

Abbildung 5.3: Zum allgemeinen Additionsgesetz.

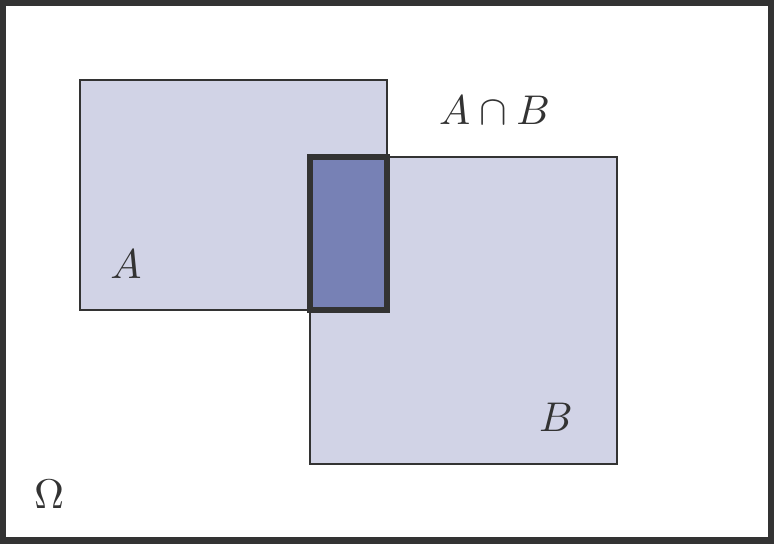
Um die Wahrscheinlichkeit zu bestimmen, dass \(A\) oder \(B\) eintritt, können wir nicht einfach die Wahrscheinlichkeiten von \(A\) und \(B\) addieren, denn im allgemeinen wird \(A\cap B\ne \varnothing\) sein. Und dann würden die Versuchsergebnisse, die zu \(A\) und \(B\) gehören zweimal berücksichtigt werden, daher müssen wir \(P(A\cap B)\) einmal subtrahieren. Das ist genau die Aussage von (5.4).

Musteraufgabe 5.15 (Lösen einer mathematischen Aufgabe) Studentin \(A\) löst eine mathematische Aufgabe mit Wahrscheinlichkeit \(3/4\), Student \(B\) hingegen nur mit Wahrscheinlichkeit \(1/2\). Die Wahrscheinlichkeit, dass beide die Aufgabe lösen, beträgt \(3/8\).

Wie wahrscheinlich ist es, dass die Aufgabe gelöst wird?

Lösung: Aus der Angabe: \(P(A)=\dfrac{3}{4},\; P(B)=\dfrac{1}{2}, \;P(A \cap B)=\dfrac{3}{8}\).

Wenn die Aufgabe gelöst wird, dann bedeutet das: \(A\) löst die Aufgabe, oder es gelingt \(B\) die Aufgabe zu lösen, oder beide schaffen das.

Wir suchen also \(P(A\cup B)\). Mit Hilfe des Additionsgesetzes (5.4): \[ \begin{aligned} P(A\cup B)&=P(A)+P(B)-P(A\cap B)\\ &=\frac{3}{4}+\frac{1}{2}-\frac{3}{8}=\frac{7}{8}=0.875\,. \end{aligned} \]

5.1.6 Zufallsgrößen

Wahrscheinlichkeiten für Ereignisse, die durch Zufallsgrößen ausgedrückt werden, kann man auf ähnliche Weise berechnen. Das Gesetz der großen Zahlen (5.1) steht uns genauso zur Verfügung wie der klassische Wahrscheinlichkeitsbegriff (5.3).

Musteraufgabe 5.16 Ein Würfel wird zweimal geworfen. Es bezeichne \(X\) die Augenzahl beim ersten Wurf und \(Y\) die Augenzahl beim zweiten Wurf. Wie groß ist \(P(X+Y<4)\)?

Lösung: Da alle \(6\cdot 6=36\) möglichen Ergebnisse (Augenpaare) von \((X,Y)\) als gleichwahrscheinlich anzusehen sind, hat jedes die Wahrscheinlichkeit \(1/36\). Es gibt genau 3 Ergebnisse, deren Augensumme kleiner als 4 ist, nämlich \[ \begin{gathered} \{X+Y<4\}=\{(1,1),(1,2),(2,1)\}. \end{gathered} \] Daher beträgt \[ \begin{gathered} P(X+Y<4)=\frac{3}{36}=0.0833\,. \end{gathered} \]

Musteraufgabe 5.17 Ein Würfel wird zweimal geworfen. Es bezeichne \(X\) die Augenzahl beim ersten Wurf und \(Y\) die Augenzahl beim zweiten Wurf. Wie groß ist \(P(X-Y=0)\)?

Lösung: Die Ergebnismenge \(\Omega\) ist die Menge aller 36 Paare \((a,b)\) mit \(a,b=1,\ldots 6\). Das Ereignis \(\{X-Y=0\}\) kann nur eintreten, wenn \(X=Y\) ist. Dafür gibt es genau 6 Möglichkeiten: \[ \begin{gathered} \{X=Y\}=\{(1,1),(2,2),(3,3),(4,4),(5,5),(6,6)\}. \end{gathered} \] Daher ist \[ \begin{gathered} P(X-Y=0)=\frac{6}{36}\simeq 0.1667\,. \end{gathered} \] □

Satz 5.18 (Satz über das Gegenereignis) Es sei \(A\) ein Ereignis, dann gilt: \[ \begin{gathered} P(A')=1-P(A). \end{gathered} \tag{5.5}\]

Begründung: Das Ereignis \(A\) und sein Gegenereignis \(A'\) sind sicherlich unvereinbar, d.h. \(A\cap A'=\varnothing\). Andererseits bildet ihre Vereinigung die Ergebnismenge \(\Omega\), also \(\Omega=A\cup A'\). Deshalb folgt aus dem Additionsgesetz (5.2): \[ \begin{gathered} P(\Omega)=1=P(A)+P(A')\implies P(A')=1-P(A). \end{gathered} \] □

Wir betrachten ein Glücksspiel, das aus einer Serie von Einzelspielen besteht, von denen jedes einzelne die möglichen Ergebnisse \(G\) (Gewinn) und \(V\) (Verlust) besitzt. Ein solches Glücksspiel nennt man symmetrisch, wenn bei jedem Einzelspiel Gewinn und Verlust gleichwahrscheinlich sind und wenn die Spielergebnisse einer Serie einander nicht beeinflussen. Unter diesen Voraussetzungen besitzen alle \(2^n\) möglichen Ergebnislisten die gleiche Wahrscheinlichkeit \(1/2^n\).

Musteraufgabe 5.19 Ein Spieler beteiligt sich an einem symmetrischen Glücksspiel und spielt 10 mal. Wir groß ist die Wahrscheinlichkeit dafür, dass er mindestens einen Gewinn erzielt?

Lösung: Es sei \(S_{10}\) die Anzahl der Gewinne in einer Spielserie der Länge \(10\). Wie groß ist \(P(S_{10}\ge 1)\)?

Dazu betrachten wir das Gegenereignis von \(\{S_{10}\ge 1\}\). Was ist das Gegenteil von {mindestens ein Gewinn in 10 Spielen}?

Ganz einfach: \(\{S_{10}\ge 1\}'=\) {von 10 Spielen wurde kein einziges gewonnen}!

Es ist also \(\{S_{10}\ge 1\}'=\{S_{10}=0\}\) und damit infolge (5.5): \[ \begin{gathered} P(S_{10}\ge 1)=1-P(S_{10}=0). \end{gathered} \] Die Wahrscheinlichkeit auf der rechten Seite ist aber leicht zu ermitteln, denn dem zugrundeliegenden Ereignis entspricht nur ein einziges Ergebnis, nämlich alle 10 Spiele zu verlieren. Das geschieht jedoch mit Wahrscheinlichkeit \(1/2^{10}\). Daraus folgt \[ \begin{gathered} P(S_{10}\ge 1)=1-\frac{1}{2^{10}}=0.9990234\,. \end{gathered} \] □

Musteraufgabe 5.20 Ein Spieler beteiligt sich an einem symmetrischen Glücksspiel. Es sei \(W\) die Wartezeit (Anzahl der Einzelspiele) bis zum ersten Gewinn. Man berechne \(P(W\le 8)\).

Lösung: Wieder argumentieren wir mit dem Gegenereignis. Es ist \[ \begin{gathered} P(W\le 8)=1-P(W>8).%=1-P(S_5=0)=1-\frac{1}{2^5}= 0.96875. \end{gathered} \] Wenn aber das Ereignis \(\{W>8\}\) eingetreten ist, dann wissen wir etwas über das Ergebnis der ersten 8 Spiele: \(W\) kann nur \(>8\) sein, wenn von den ersten 8 Spielen kein einziges gewonnen wurde. Andernfalls wäre \(W\le 8\). Mit anderen Worten: \[ \begin{gathered} P(W\le 8)=1-P(W>8)=1-P(S_8=0)=1-\frac{1}{2^8}=0.9961\,. \end{gathered} \]

Musteraufgabe 5.21 (Ein Paradox) Wie groß ist die Wahrscheinlichkeit, dass in einer Gruppe von 10 Personen wenigstens zwei am selben Tag Geburtstag haben (egal, in welchem Jahr)?

Lösung: Wir repräsentieren einen Geburtstag durch eine natürliche Zahl zwischen 1 und 365. D.h. 1 entspricht dem 1. Januar, usw. Die Ergebnismenge \(\Omega\) ist die Menge aller möglichen 10-er Listen von Zahlen aus \(1,2,\ldots,365\). Und dabei dürfen natürlich Geburtstage mehrfach vorkommen. Es könnte ja sein, dass alle 10 Personen am 1. Januar Geburtstag haben. Die Mächtigkeit von \(\Omega\) ist daher: \[ \begin{gathered} |\Omega|=\underbrace{365\cdot 365\cdots 365}_{\text{10 mal}}=365^{10}=4.2\cdot 10^{25}. \end{gathered} \] Es sei \(A\) das Ereignis, dass wenigstens zwei Personen am selben Tag Geburtstag haben. Was ist dann \(A'\)?

\(A'\) ist das Ereignis, dass alle 10 Geburtstage verschieden sind! Die Mächtigkeit von \(A'\) ist aber leicht zu finden.

Wir bilden 10-er Listen, wobei wir für den ersten Platz 365 Möglichkeiten haben, für den zweiten Platz nur mehr 364 (denn die Geburtstage sollen verschieden sein), usw.: \[ \begin{gathered} |A'|=365\cdot 364\cdot 363\cdots 356 = 3.7\cdot 10^{25}. \end{gathered} \] Und damit erhalten wir: \[ \begin{gathered} P(A)=1-\frac{3.7\cdot 10^{25}}{4.2\cdot 10^{25}}\simeq 0.12\,. \end{gathered} \] Diese Wahrscheinlichkeit ist überraschend hoch. Noch deutlicher wird das, wenn wir eine Gruppe von 50 Personen betrachten. In diesem Fall ist die Wahrscheinlichkeit, dass wenigstens zwei Personen am selben Tag Geburtstag haben, \[ \begin{gathered} P(A)=1-\frac{3.9\cdot 10^{126}}{1.3\cdot 10^{128}}\simeq 0.97\,. \end{gathered} \] Es ist also sehr wahrscheinlich, dass sich unter 50 Personen wenigstens zwei Personen mit dem gleichen Geburtstag finden lassen. Oder anders gesagt: es ist sehr unwahrscheinlich, dass bei 50 Personen alle Geburtstage verschieden sind. □

5.1.7 Diskrete Verteilungen

Alle Zufallsgrößen, die wir bisher untersucht haben, sind diskrete Zufallsgrößen. Damit meinen wir, dass die Menge ihrer möglichen Werte abzählbar ist. Entweder war diese Wertemenge \(\mathcal S\) endlich, oder sie hatte nicht mehr Elemente, als es natürliche Zahlen gibt.

In Musteraufgabe 5.16: \[ \begin{gathered} X\in\mathcal S_X,Y\in\mathcal S_Y,\quad \mathcal S_X,\mathcal S_Y=\{1,2,3,4,5,6\},\\ Z=X+Y\in \mathcal S_{Z}=\{2,3,4,\ldots,12\}. \end{gathered} \] In Musteraufgabe 5.17: \[ \begin{gathered} X\in\mathcal S_X,Y\in\mathcal S_Y,\quad \mathcal S_X,\mathcal S_Y=\{1,2,3,4,5,6\},\\ Z=X-Y\in\mathcal S_Z=\{-5,-4,-3,\ldots,3,4,5\}. \end{gathered} \] In Musteraufgabe 5.19: \[ \begin{gathered} S_{10}\in\mathcal S=\{0,1,2,\ldots,10\}. \end{gathered} \] In Musteraufgabe 5.20 war der Wertebereich erstmals unendlich groß: \[ \begin{gathered} W\in\mathcal S=\{1,2,3,\ldots\}=\mathbb N. \end{gathered} \] Für alle diese und viele weitere Beispiele ist es problemlos möglich eine Funktion \(f_X(x)=P(X=x)\) für alle Werte von \(x\in \mathcal S\) anzugeben. Diese Funktion nennt man Wahrscheinlichkeitsfunktion der Zufallsgröße \(X\). Wir können sie durch Funktionsterme oder auch in Form von Wertetabellen darstellen.

Beispielsweise Musteraufgabe 5.16, hier ist \(Z=X+Y\): \[ \begin{gathered} f_X(x)=f_Y(x)=\frac{1}{6},\quad x=1,2,\ldots 6\\ \begin{array}{c|ccccccccccc} z & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12\\ \hline\\[-10pt] f_Z(z) & \frac{1}{36} &\frac{2}{36} & \frac{3}{36} & \frac{4}{36} & \frac{5}{36} & \frac{6}{36} & \frac{5}{36} & \frac{4}{36} & \frac{3}{36} & \frac{2}{36} & \frac{1}{36} \end{array}\ \end{gathered} \tag{5.6}\] Neben der Wahrscheinlichkeitsfunktion benötigen wir auch das Konzept der Verteilungsfunktion \(F(x)\) einer Zufallsgröße. Sie ist definiert durch: \[ \begin{gathered} F(x)=P(X\le x)=\sum_{u\le x}f(u). \end{gathered} \tag{5.7}\] Das ist die kumulative Summe der Werte der Wahrscheinlichkeitsfunktion. Im Gegensatz zu \(f(x)\) ist die Verteilungsfunktion \(F(x)\) für alle reellen Zahlen \(x\) definiert. Sie erlaubt uns interessante Fragen direkt zu beantworten.

Nehmen wir als Beispiel die Zufallsgröße \(Z=X+Y\), deren Wahrscheinlichkeitsfunktion in (5.6) gegeben ist. Aus ihr errechnen wir: \[ \begin{aligned} F_Z(2)&=P(Z\le 2)=P(Z=2)=\frac{1}{36}\\[4pt] F_Z(3)&=P(Z\le 3)= P(Z=2)+P(Z=3)=\frac{3}{36}\\[4pt] F_Z(4)&=P(Z\le 4)=P(Z=2)+\ldots+P(Z=4)=\frac{6}{36}\\[4pt] &\ldots\\ F_Z(12)&=P(Z\le 12)=P(Z=2)+\ldots+P(Z=12)=1\ \end{aligned} \tag{5.8}\] Übersichtlicher stellen wir \(F_Z(z)\) tabellarisch dar: \[ \begin{gathered} \begin{array}{c|ccccccccccc} z & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12\\ \hline\\[-10pt] f_Z(z) & \frac{1}{36} &\frac{2}{36} & \frac{3}{36} & \frac{4}{36} & \frac{5}{36} & \frac{6}{36} & \frac{5}{36} & \frac{4}{36} & \frac{3}{36} & \frac{2}{36} & \frac{1}{36} \\[4pt] F_Z(z) & \frac{1}{36} & \frac{3}{36} & \frac{6}{36} & \frac{10}{36} & \frac{15}{36} & \frac{21}{36} & \frac{26}{36} & \frac{30}{36} & \frac{33}{36} & \frac{35}{36} & 1 \end{array} \end{gathered} \] Nun sagten wir eben, die Verteilungsfunktion \(F(x)\) ist für alle reellen Zahlen definiert. Diese Eigenschaft kommt in der tabellarischen Darstellung (5.8) nicht so deutlich zum Ausdruck. Tatsächlich ist die Verteilungsfunktion einer diskreten Zufallsgröße eine Treppenfunktion. (5.8) lautet daher so (die Wert als gerundete Gleitkommazahlen): \[ \begin{gathered} F_Z(z)=P(Z\le z)=\left\{\begin{array}{cl} 0.000 & \text{für } z<2\\[4pt] 0.028 & 2\le z < 3\\[4pt] 0.083 & 3\le z < 4\\[4pt] 0.167 & 4\le z < 5\\[4pt] 0.278 & 5\le z < 6\\ \vdots &\\ 0.972 & 11\le z < 12\\[4pt] 1.000 & z\ge 12 \end{array} \right. \end{gathered} \tag{5.9}\] Diese Funktion ist in Abbildung 5.4 dargestellt.

Abbildung 5.4: Verteilungsfunktion \(F_Z(z)\) zu (5.9).

Diese Abbildung zeigt uns, dass eine diskrete Verteilungsfunktion Sprünge aufweist und zwar an jenen Stellen \(x\) für die \(f(x)>0\). Zwischen den Sprüngen ist die Verteilungsfunktion konstant.

Wir können z.B. ablesen: \[ \begin{gathered} F_Z(5.5)=P(Z\le 5.5)=P(Z\le 5)=\frac{10}{36}\simeq 0.278 \end{gathered} \] Die Verteilungsfunktion verdichtet wichtige Information: \[ \begin{aligned} %% {alignat*}{2} P(X>a)&=1-P(X\le a)&=&\;1-F(a),\\[4pt] P(a<X\le b)&=P(X\le b)-P(X\le a)&=&\;F(b)-F(a). \end{aligned} \] Diese Eigenschaften gelten auch unter viel allgemeineren Umständen, sodass wir in Form eines Satzes zusammenfassen:

Satz 5.22 (Eigenschaften der Verteilungsfunktion)  

• Die Verteilungsfunktion \(F(x)\) ist für alle reellen Zahlen definiert.

• \(0\le F(x)\le 1\).

• \(F(x)\) nimmt monoton zu.

• \(\lim_{x\to- \infty}F(x)=0\), \(\lim_{x\to\infty}F(x)=1\).

• \(P(X\le a)=F(a)\).

• \(P(X>a)=1-F(a)\).

• \(P(a<X\le b)=F(b)-F(a)\).

Musteraufgabe 5.23 Es ist \(N\) die Anzahl der Maschinenausfälle pro Tag in einer Offsetdruckerei. Die Wahrscheinlichkeitsfunktion von \(N\) wurde aus in der Vergangenheit gesammelten Daten geschätzt: \[ \begin{gathered} \begin{array}{c|cccccc} n & 0 & 1 & 2 & 3 & 4 & 5\\ \hline\\[-10pt] P(N=n) & 0.224 & 0.336 & 0.252 & 0.126 & 0.047 & 0.015 \end{array} \end{gathered} \] Mehr als 5 Ausfälle pro Tag sind nie beobachtet worden.

Bestimmen Sie die Verteilungsfunktion von \(N\).

Was ist die Wahrscheinlichkeit von mehr als 3 Ausfällen pro Tag?

Lösung: Die Verteilungsfunktion \(F(n)=P(N\le n)\) ergibt sich aus den kumulativen Werten der Wahrscheinlichkeitsfunktion: \[ \begin{gathered} \begin{array}{c|cccccc} n & 0 & 1 & 2 & 3 & 4 & 5\\ \hline\\[-10pt] P(N=n) & 0.224 & 0.336 & 0.252 & 0.126 & 0.047 & 0.015\\[3pt] P(N\le n)& 0.224 & 0.560 & 0.812 & 0.938 & 0.985 & 1.000 \end{array} \end{gathered} \] Die Wahrscheinlichkeit, mehr als 3 Ausfälle an einem Tag zu beobachten ist: \[ \begin{gathered} P(N>3)=1-P(N\le 3)=1-0.938 = 0.062\,. \end{gathered} \] □

5.1.8 Stetige Verteilungen

Diskrete Zufallsgrößen nehmen ihre Werte in einer endlichen oder abzählbar unendlichen Menge an. Sehr häufig drücken sie Zählergebnisse aus, wie die Anzahl der gewonnenen Spiele, die Zahl der wartenden Kunden vor einem Check in-Schalter am Flughafen, die Anzahl der Maschinenausfälle pro Tag, die Zahl der Kinder pro Familie, usw.

Daneben gibt es eine weitere Klasse von Zufallsgrößen, die ihre Werte in einem Intervall annehmen. Sie entstehen typischerweise nicht durch Zählungen, sondern durch Messungen, die in ganz konkreten Messwerten resultieren. Hier einige Beispiele:

• Wartezeiten von Kunden, Lebensdauer von Produkten, usw.

• Entfernungen, Längen, Gewichte, usw.

• Renditen von Finanzanlagen
  und vieles andere mehr.

Der Wert \(P(t)\) eines Portfolios zur Zeit \(t\) wird in Währungseinheiten angegeben und ist in strengem Sinn eine diskrete Größe. Aber da der Wertebereich von \(P(t)\) in der Regel sehr groß ist im Verhältnis zu kleinsten Währungseinheit (z.B. ein Eurocent), wird man \(P(t)\) approximativ als stetige Größe behandeln.

Ereignisse, die wir mit Hilfe von stetigen Zufallsgrößen ausdrücken, sind nun nicht mehr Punktereignisse, wie z.B. \(\{X=5\}\), sondern Intervalle auf der Zahlengeraden.

Um solchen Intervallen Wahrscheinlichkeiten zuzuordnen, benötigen wir das Konzept der Dichtefunktion.

Die Dichte einer stetigen Zufallsgröße \(X\) ist eine stetige Funktion \(f(x)\) mit \[ \begin{gathered} f(x)\ge 0,\qquad \int_{-\infty}^\infty f(x)\,\mathrm{d}x = 1. \end{gathered} \] Die letzte Forderung besagt (siehe Kapitel 4), dass die Fläche unterhalb der Dichte gleich 1 sein muss. Tatsächlich sind es Flächen unterhalb von \(f(x)\), die Wahrscheinlichkeiten angeben. Insbesondere ist \[ \begin{gathered} F(a)=P(X\le a)=\int_{-\infty}^af(x)\,\mathrm{d}x. \end{gathered} \] Die Funktion \(F(x)\) nennt man wie im Falle diskreter Zufallsgrößen Verteilungsfunktion von \(X\). Sie besitzt alle in Satz 5.22 formulierten Eigenschaften. Insbesondere haben wir: \[ \begin{aligned} P(X>a)&=\int_a^\infty f(x)\,\mathrm{d}x=1-F(a),\\[5pt] P(a<X\le b)&= \int_a^bf(x)\,\mathrm{d}x=F(b)-F(a). \end{aligned} \] Abbildung 5.5 veranschaulicht diese Beziehungen.

Abbildung 5.5: Dichte und Wahrscheinlichkeiten.

Überdies ist die Verteilungsfunktion einer stetigen Zufallsgröße in allen Punkten, in denen die Dichte \(f(x)\) stetig ist, differenzierbar und es gilt: \[ \begin{gathered} f(x)=F'(x). \end{gathered} \tag{5.10}\] Es ist wichtig zu betonen, dass die Funktionswerte der Dichtefunktion \(f(x)\) keine Wahrscheinlichkeiten sind. Wohl aber gilt (Prinzip der lokalen Linearisierung, Kapitel 3, siehe auch Abbildung 5.6) für sehr kleine Werte von \(h>0\): \[ \begin{gathered} P(x< X\le x+h)\approx f(x) h. \end{gathered} \tag{5.11}\]

Abbildung 5.6: Illustration des Prinzips der lokalen Linearisierung.

Dies hat aber noch eine wichtige Konsequenz, die Anlass gibt zu einer weiteren charakteristischen Eigenschaft stetiger Zufallsgrößen. Wenn wir nämlich \(h\to 0\) gehen lassen und \(a\) keine Unstetigkeitsstelle (Sprungstelle) der Dichte ist, dann \[ \begin{gathered} \lim_{h\to 0} P(a<X\le a+h)=P(X=a)=0. \end{gathered} \tag{5.12}\] Diese Eigenschaft ist sehr merkwürdig, dennoch typisch für stetige Zufallsgrößen. Wir haben zwar in Satz 5.9 gefordert, dass dem unmöglichen Ereignis die Wahrscheinlichkeit Null zugeordnet wird, aber offensichtlich ist die Umkehrung dieser Aussage nicht richtig. Boris Gnedenko (1912–1995), ein bedeutender russischer Wahrscheinlichkeitstheoretiker hat versucht seinen Studentinnen und Studenten diesen Sachverhalt so zu erklären: wir müssen unterscheiden zwischen theoretischer Unmöglichkeit eines Ereignisses (z.B. mit einem 6-seitigen Würfel eine 7 zu werfen), und faktischer Unmöglichkeit. Nehmen wir etwa an, \(X\) wäre die Lebensdauer einer Energiesparlampe. Offensichtlich nimmt \(X\) seine Werte in dem Intervall \([0,\infty)\) an. Natürlich ist es theoretisch möglich, dass \(X=1000\) Stunden hält. Aber faktisch ist dies unmöglich, also \(P(X=1000)=0\).

Ein intuitives Argument, das den formalen Aspekt (5.12) unterstützt, wäre dieses: Die Aussage \(\{X=1000\}\) besagt unter anderem, dass der Wert der Zufallsgröße nicht 1000.00000000001 und auch nicht 999.999999999999 beträgt. Wenn wir also eine Wette auf das Ereignis \(\{X=1000\}\) abschließen, dann würden wir diese Wette verlieren, wenn sich der Wert der Zufallsgröße \(X\) um einen ganz geringen, praktisch nicht messbaren Betrag von 1000 unterscheidet. Da dies praktisch immer der Fall sein wird, werden wir die Wette immer verlieren. Nichts anderes ist der Inhalt der Gleichung \(P(X=1000)=0\).

Beispiel 5.24 (Exponentialverteilung)

Die Exponentialverteilung ist eine der wichtigsten stetigen Verteilungen. Wir sagen, eine Zufallsgröße \(T\) ist exponentialverteilt, wenn ihre Dichte gegeben ist durch: \[ \begin{gathered} f(t)=\left\{\begin{array}{cl} 0 & t<0\\ \lambda e^{-\lambda t} & t\ge 0 \end{array}\right.,\qquad \lambda >0 \end{gathered} \tag{5.13}\] Der Parameter \(\lambda\) wird Ereignisrate genannt, und diese Wortwahl deutet auch schon in die Richtung der wichtigsten Anwendungen der Exponentialverteilung. Sie wird gerne verwendet, um Zeitabstände \(T\) zwischen zufälligen Ereignissen zu modellieren. Diese Ereignisse können sein:

• Ankünfte von Kunden im weitesten Sinn, z. B. Passagiere am Flughafen, Kunden einer Bank;

• Ausfälle von technischen Anlagen: Die Zeit zwischen zwei Ausfällen einer Maschine, ihre up-time, ist häufig exponentialverteilt.

• Die Zeitabstände zwischen Emissionen von \(\alpha\)-Teilchen durch einen Atomkern: das war sogar die ursprüngliche Anwendung der Exponentialverteilung Anfang des 20. Jahrhunderts.

Die Verteilungsfunktion ermitteln wir auf einfache Weise mit den Methoden, die wir in Kapitel 4 kennengelernt haben: \[ \begin{gathered} P(T\le t)=F(t)=\int_0^t\lambda e^{-\lambda s}\,\mathrm{d}s=-e^{-\lambda s}\bigg|_0^t=1-e^{-\lambda t},\qquad t\ge 0. \end{gathered} \] Die Dichte besitzt eine Unstetigkeit (Sprungstelle) in \(t=0\), die Verteilungsfunktion hat an dieser Stelle einen Knick und ist dort nicht differenzierbar. Aber für alle \(t>0\) ist \(F'(t)=f(t)\), wie die Leser nachprüfen sollten.

Die Ereignisrate \(\lambda\) ist so zu interpretieren: ihr Wert sagt uns, wie dicht die Ereignisse aufeinander folgen. Je größer \(\lambda\), umso kleiner ist der mittlere Abstand der Ereignisse, umso dichter folgen sie aufeinander. Je kleiner \(\lambda\), umso weniger dicht folgen die Ereignisse aufeinander, ihre mittleren Abstände sind entsprechend größer.

Abbildung 5.7: Dichte \(f(t)\) und Verteilung \(F(t)\) einer Exponentialverteilung mit \(\lambda =1\).

Musteraufgabe 5.25 (Krankenhausmanagement) Aus Untersuchungen in den Vereinigten Staaten ist bekannt, dass die Verweilzeit (in Tagen) von Patienten in Intensivstationen (ICUs) in sehr guter Näherung exponentialverteilt ist mit \(\lambda=0.2564\). Dies entspricht einer mittleren Verweilzeit von 3.9 Tagen.

1. Was ist der Anteil der Patienten, die länger als 10 Tage auf einer ICU verbringen müssen?

2. Welche kritische Verweilzeit wird von 1 % der Patienten überschritten?

Lösung:
(a) Es sei \(T\) die Verweilzeit. \[ \begin{aligned} P(T>10)&=1 - P(T\le 10)\\ &=1 -(1-e^{-10\cdot 0.2564})=e^{-2.564}= 0.076996 \simeq 0.077\,. \end{aligned} \] Etwa 7.7 % der Patienten bleiben länger als 10 Tage auf der ICU.

(b) Wir suchen eine Zeitspanne \(t\), sodass \(P(T>t)=0.01\): \[ \begin{gathered} P(T>t)=e^{-0.2564 t}=0.01\\ \implies t=-\frac{\ln(0.01)}{0.2564} =17.961 \simeq 18\text{ Tage}. \end{gathered} \] □

Beispiel 5.26 (Logistische Verteilung)

Eine Zufallsgröße \(X\) heißt logistisch verteilt, wenn sie folgende Verteilungsfunktion und Dichte besitzt: \[ \begin{aligned} F(x)&=P(X\le x)=\frac{1}{1+e^{-(x-\mu)/s}},\qquad x\in\mathbb R\\[5pt] f(x)&=\frac{e^{-(x-\mu)/s}}{2\left(1+e^{-(x-\mu)/s}\right)^2}\,.\ \end{aligned} \tag{5.14}\] Der Parameter \(\mu\) ist (siehe Abschnitt 5.3.1) und gibt die Lage des Maximums der Dichte \(f(x)\) an, \(s\) ist ein Skalenparameter. Die Anwendungen der Logistischen Verteilung sind vielfältig, sie reichen von statistischer Datenanalyse über technische Zuverlässigkeit bis hin zur Finanzmathematik. So gibt es gute (statistische) Gründe die Logistische Verteilung zur Modellierung von Renditen von Finanzanlagen zu verwenden.

Abbildung 5.8: Dichte \(f(x)\) und Verteilungsfunktion \(F(x)\) einer logistischen Verteilung mit \(\mu =2\) und \(s=1\).

Musteraufgabe 5.27 (Finanzmathematik) Die jährliche Rendite \(X\) eines Wertpapiers ist logistisch verteilt mit \[ \begin{gathered} P(X\le x)=\frac{1}{1+e^{-(x-0.1)/0.022}}. \end{gathered} \] Zu Beginn eines Jahres wurden 2000 GE in das Wertpapier investiert.

1. Wie groß ist die Wahrscheinlichkeit, dass der Gewinn am Ende des Jahres mehr als 300 GE beträgt?

2. Wie groß ist die Wahrscheinlichkeit, dass die Rendite negativ und damit Kapital verloren wird?

Lösung: (a) Da der Gewinn \(G=2000X\) beträgt: \[ \begin{gathered} G>300\Leftrightarrow 2000X>300 \implies X>\frac{300}{2000}=0.15\,. \end{gathered} \] Daher: \[ \begin{aligned} P(X>0.15) & = 1-P(X\le 0.15) \\ & = 1-\frac{1}{1+e^{-(0.15-0.1)/0.022}}=0.093407\,. \end{aligned} \] Die Wahrscheinlichkeit dafür beträgt somit ca. 9.3 %.

(b) Wir suchen \(P(X\le 0)\): \[ \begin{gathered} P(X\le 0)=\frac{1}{1+e^{-(0-0.1)/0.022}}=0.010504. \end{gathered} \] Dieses unerfreuliche Szenario tritt also mit Wahrscheinlichkeit von ca. 1 % ein. □

5.2 Bedingte Wahrscheinlichkeiten

5.2.1 Vierfeldertafeln

Es seien \(A\) und \(B\) zwei Ereignisse in Zusammenhang mit einem Zufallsexperiment. Wir können uns auch vorstellen, es handle sich um zwei Teilmengen einer endlichen Grundgesamtheit.

Wir führen das Zufallsexperiment durch (z.B. Ziehen eines Elements der Grundgesamtheit) und registrieren, welche der beiden Ereignisse eintreten. Die möglichen Kombinationen von Ereignissen stellen wir in einer Tabelle zusammen: \[ \begin{gathered} \begin{array}{c|cc} & B & B' \\ \hline A & A\cap B & A\cap B' \\ A' & A'\cap B & A'\cap B'\\ \end{array} \end{gathered} \] Dabei bezeichnet \(A'\) wie üblich das Gegenereignis von \(A\).

Versieht man diese Tabelle mit den entsprechenden Wahrscheinlichkeiten, dann erhält man eine Vierfeldertafel oder Kontingenztafel. Man kann an den Rändern der Tabelle die Wahrscheinlichkeiten der Einzelereignisse eintragen, die sich nach dem Additionsgesetz als Zeilen- bzw. Spaltensummen berechnen lassen. \[ \begin{gathered} \begin{array}{c|cc|c} & B & B' &\\ \hline A & P(A\cap B) & P(A\cap B') & P(A) \\ A' & P(A'\cap B) & P(A'\cap B') & P(A')\\ \hline & P(B) & P(B') & 1 \end{array} \end{gathered} \] Die Wahrscheinlichkeiten, die sich als Zeilen- und Spaltensummen ergeben, nämlich \(P(A), P(A'), P(B)\) und \(P(B')\), heißen totale Wahrscheinlichkeiten. So ist \[ \begin{gathered} P(A)=P(A\cap B) + P(A\cap B') \end{gathered} \] die totale Wahrscheinlichkeit des Ereignisses \(A\). Wir meinen damit die Wahrscheinlichkeit für das Eintreten von \(A\), unabhängig davon, ob es mit \(B\) oder seinem Gegenereignis eingetreten ist. Dahinter steckt natürlich das fundamentale Additionsgesetz (5.2), denn die Ereignisse \(\{A\cap B\}\) und \(\{A\cap B'\}\) sind sicherlich unvereinbar: \[ \begin{gathered} (A\cap B)\cap (A\cap B')=A\cap B\cap B'=\varnothing, \end{gathered} \] weil \(B\cap B'=\varnothing\). Die totalen Wahrscheinlichkeiten für \(A', B\) und \(B'\) ergeben sich analog.

Um eine Vierfeldertafel vollständig auszufüllen, benötigt man lediglich drei voneinander unabhängige Angaben.

Beispiel 5.28 (Der ELISA Test)

ELISA (Enzyme-linked Immunosorbent Assay) ist ein seit Mitte der 1980er Jahre verfügbares Verfahren um Antikörper gegen das HI-Virus in menschlichem Blut nachzuweisen. Es ist ein vergleichsweise kostengünstiger Test, der für das Screening von Blutbanken verwendet wird, aber auch um Gruppen von Menschen, wie z.B. Rekruten beim Militär, auf HIV zu testen. ELISA ist ein Suchtest, d.h. er wird vor allem eingesetzt, um möglichst alle mit dem HI-Virus infizierten Personen einer Gruppe bzw. deren Blutspenden identifizieren zu können.

Wir definieren für dieses Beispiel die folgenden beiden Ereignisse: \[ \begin{aligned} A &= \text{\{eine Person ist mit dem HI Virus infiziert}\\ &\phantom{=~\{} \text{und hat Antikörper gegen das Virus gebildet\}},\\[5pt] B &=\text{\{ELISA liefert ein positives Testergebnis\}}. \end{aligned} \] In einer groß angelegten Untersuchung (\(>\) 50000 Probanden) wurden folgende Wahrscheinlichkeiten geschätzt: \[ \begin{gathered} \begin{array}{l|cc|r} & B & B' &\\ \hline A & 0.0038 & 0.0002 & 0.0040\\ A'& 0.0301 & 0.9659 & 0.9960\\ \hline & 0.0339 & 0.9661 & 1.0000 \end{array} \end{gathered} \] Was sagen uns diese Daten?

• Der Anteil der HIV-Infizierten an der Gesamtpopulation, die Prävalenz von HIV, beträgt \(P(A)=0.004\), also 0.4 %.

• Der Anteil der positiv getesteten Probanden beträgt \(P(B)=0.0339\).

• Mit einer Wahrscheinlichkeit von \(P(A\cap B')=0.0002\) war ein Proband mit dem HI-Virus infiziert und hatte ein negatives Testergebnis.

• Mit Wahrscheinlichkeit \(P(A'\cap B)=0.0301\) war ein Proband nicht infiziert und hatte dennoch ein positives Testergebnis.

Dies sind Informationen, die unmittelbar aus der Kontingenztafel ablesbar sind.

Aber in dieser Tabelle steckt noch mehr.

Definition 5.29 (Bedingte Wahrscheinlichkeit) Es seien \(A\) und \(B\) Ereignisse mit \(P(B)>0\), dann ist \[ \begin{gathered} P(A|B)=\frac{P(A\cap B)}{P(B)} \end{gathered} \tag{5.15}\] die bedingte Wahrscheinlichkeit des Ereignisses \(A\) unter der Bedingung \(B\).

Diese Definition gibt uns Antwort auf die Frage: Unter wievielen Fällen, bei denen das Ereignis \(B\) eintritt, tritt zusätzlich auch das Ereignis \(A\) ein?

Die Formel (5.15) ist leicht zu verstehen, wenn man sie als Aussage über Anteile in endlichen Grundgesamtheiten interpretiert: Die bedingte Wahrscheinlichkeit ist identisch mit dem Anteil von \(A\) an der Gesamtheit \(B\).

Wir setzen Beispiel 5.28 fort.

Beispiel 5.30 (Fortsetzung von Beispiel 5.30)

Wir berechnen zuerst \(P(A|B)\). Das ist die Wahrscheinlichkeit dafür, dass jemand, der mittels ELISA positiv getestet wurde (Ereignis \(B\)), tatsächlich Träger des HI-Virus ist (Ereignis \(A\)). Mit (5.15) erhalten wir: \[ \begin{gathered} P(A|B)=\frac{P(A\cap B)}{P(B)}=\frac{0.0038}{0.0339}=0.1121\,. \end{gathered} \] Das ist interessant: jemand, der positiv getestet wurde ist nur mit einer Wahrscheinlichkeit von ca. 11 % tatsächlich mit dem HI-Virus infiziert.

Nun berechnen wir \(P(B|A)\), dies ist der Anteil der positiv Getesteten (Ereignis \(B\)) an den HIV-Infizierten (Ereignis \(A\)): \[ \begin{gathered} P(B|A)=\frac{P(A\cap B)}{P(A)}=\frac{0.0038}{0.0040}=0.95\,. \end{gathered} \] Diese Wahrscheinlichkeit nennt man im medizinischen Kontext Sensitivität des Tests. Naturgemäß möchte man, dass diese Wahrscheinlichkeit möglichst groß ist, denn das ist die Wahrscheinlichkeit, dass ein HIV-Infizierter tatsächlich mit ELISA entdeckt wird.

Ein weiterer interessanter Wert ist \(P(B'|A')\): \[ \begin{gathered} P(B'|A')=\frac{P(A'\cap B')}{P(A')}=\frac{0.9659}{0.9960}=0.9698\,. \end{gathered} \] Das ist die Wahrscheinlichkeit, dass jemand, der nicht HIV-infiziert ist ein negatives Testergebnis haben wird, die Spezifität von ELISA. Auch hier ist klar, dass man möglichst große Werte für diese Wahrscheinlichkeit erreichen möchte. Die Spezifität von ELISA beträgt hier ca. 97 %.

Und zum Abschluss noch \(P(A'|B')\). Wie sicher kann jemand, der negativ getestet wurde, sein, dass er nicht mit HIV infiziert ist? \[ \begin{gathered} P(A'|B')=\frac{P(A'\cap B')}{P(B')}=\frac{0.9659}{0.9661}=0.9998\,. \end{gathered} \] Dies ist ein beruhigender Wert.

Aus der Definition der bedingten Wahrscheinlichkeit (Definition 5.29) folgt eine wichtige Formel. Sie erlaubt uns, die Wahrscheinlichkeit, dass zwei Ereignisse gemeinsam eintreten, mit Hilfe der bedingten Wahrscheinlichkeit auszudrücken:

Satz 5.31 (Produktformel) Es gilt die Produktformel: \[ \begin{gathered} P(A\cap B)=P(A|B)P(B). \end{gathered} \tag{5.16}\] Diese Formel wird auch Multiplikationssatz genannt.

In manchen Fragestellungen sind die bedingten Wahrscheinlichkeiten bekannt, aber andere Wahrscheinlichkeiten fehlen. In solchen Fällen müssen die fehlenden Wahrscheinlichkeiten aus den bedingten Wahrscheinlichkeiten berechnet werden. Hierzu verwenden wir die Produktformel (5.16).

Musteraufgabe 5.32 (Das typische Frauenauto ist klein und rosa) In einer in Deutschland 2013 durchgeführten Studie wurden Verhaltensunterschiede zwischen Männern und Frauen beim Kauf eines Neuwagens untersucht. Im Jahr 2013 wurden 24% der Neuwagen von Frauen erworben, 76% von Männern. Firmenwagen wurden in der Erhebung nicht berücksichtigt.

Das Augenmerk der Untersuchung galt unter anderem dem verbreiteten Vorurteil, Frauen würden Kleinwagen bevorzugen. Zu diesem Zweck wurden die PKWs eingeteilt in Kleinwagen \(K\) und Nicht-Kleinwagen \(K'\) (Limousinen, Kombis, SUVs, usw.).

Es wurde festgestellt, dass immerhin 10% der Männer sich vorstellen können, einen Kleinwagen zu kaufen, während es bei Frauen 28% waren.

1. Wieviel Prozent der verkauften PKWs sind Kleinwagen?

2. Wieviel Prozent der Kleinwagenkäufer sind männlich?

Lösung: Wir definieren zuerst die uns interessierenden Ereignisse: \[ \begin{aligned} K & =\{\text{ein Kleinwagen wird gekauft}\},\\ F & =\{\text{Käufer ist weiblich}\},\\ M & =\{\text{Käufer ist männlich}\}. \end{aligned} \] Die Angabe verrät uns, dass der Anteil der Kleinwagenkäufer bei den Männern 10% beträgt, bei den Frauen ist dieser Anteil 28%. Daher kennen wir zwei bedingte Wahrscheinlichkeiten: \[ \begin{gathered} P(K|M)=0.1,\quad P(K|F)=0.28\,. \end{gathered} \] Außerdem wissen wir: \[ \begin{gathered} P(F)=0.24,\quad P(M)=1-P(F)=0.76. \end{gathered} \] Mit Hilfe der Produktformel (5.16) können wir nun berechnen: \[ \begin{aligned} P(K\cap M)&= P(K|M)P(M)=0.1\cdot 0.76=0.076,\\ P(K\cap F)&= P(K|F)P(F)=0.28\cdot 0.24=0.0672\,. \end{aligned} \] Damit haben wir das Grundgerüst für eine Vierfeldertafel: \[ \begin{gathered} \begin{array}{l|cc|c} &M & F\\ \hline K & 0.0760 & 0.0672 &\\ K'& & &\\ \hline & 0.7600 & 0.2400 & 1.0000 \end{array} \end{gathered} \] Die fehlenden Werte lassen sich leicht durch Ergänzen der Zeilen und Spalten finden, sodass wir schließlich die folgende vollständige Vierfeldertafel haben: \[ \begin{gathered} \begin{array}{l|cc|c} &M & F\\ \hline K & 0.0760 & 0.0672 & 0.1432\\ K'& 0.6840 & 0.1728 & 0.8568\\ \hline & 0.7600 & 0.2400 & 1.0000 \end{array} \end{gathered} \] Nun können wir die gestellten Fragen beantworten.

Der Marktanteil der Kleinwagen beträgt 14.3%, denn \(P(K)=0.1432\).

Der Anteil der Männer an den Kleinwagenkäufern ist: \[ \begin{gathered} P(M|K)=\frac{P(M\cap K)}{P(K)}=\frac{0.0760}{0.1432}=0.5307\,. \end{gathered} \] Immerhin, 53 % der Kleinwagen werden von Männern gekauft! Wieviele davon rosa waren, darüber sagen die Daten allerdings nichts. □

5.2.2 Unabhängige Ereignisse

Es kann sein, dass für zwei Ereignisse \(A\) und \(B\) die Beziehung \[ \begin{gathered} P(A|B)>P(A) \end{gathered} \] gilt. In diesem Fall könnte man sagen, das Ereignis \(B\) begünstigt das Eintreten von \(A\). Allerdings ist diese Formulierung insofern irreführend, als sie eine kausale Wirkung von \(B\) auf \(A\) nahelegt. In Wirklichkeit ist die Ungleichung völlig symmetrisch in \(A\) und \(B\), wie man aus \[ \begin{gathered} P(A|B)>P(A) \Leftrightarrow P(A\cap B)>P(A)P(B) \Leftrightarrow P(B|A)>P(B) \end{gathered} \] sehen kann. Es ist also zutreffender, wenn man sagt, dass in diesem Fall die beiden Ereignisse \(A\) und \(B\) einander begünstigen oder positiv gekoppelt sind.

Analog sagt man im Fall von \[ \begin{gathered} P(A|B)<P(A) \Leftrightarrow P(A\cap B)<P(A)P(B) \Leftrightarrow P(B|A)<P(B), \end{gathered} \] dass die beiden Ereignisse einander behindern oder negativ gekoppelt sind.

Musteraufgabe 5.33 (Unfallstatistik) Von 1000 Verkehrsunfällen sind 280 tödlich verlaufen (Ereignis \(A\)) und 100 ereigneten sich bei einer Geschwindigkeit von mehr als 150 km/h (Ereignis \(B\)). 20 Unfälle verliefen nicht tödlich und ereigneten sich bei Geschwindigkeiten über 150 km/h.

1. Wie groß ist die Wahrscheinlichkeit dafür, dass ein Hochgeschwindigkeitsunfall tödlich verläuft?

2. Wie groß ist die Wahrscheinlichkeit dafür, dass sich ein tödlicher Unfall bei hoher Geschwindigkeit ereignet hat?

3. Beurteilen Sie die Kopplung der Ereignisse \(A\) und \(B\). Versuchen Sie eine kausale Interpretation der Kopplung.

Lösung: Die absoluten Häufigkeiten betragen: \[ \begin{gathered} \begin{array}{c|cc|c} & B & B' &\\ \hline A & & & 280\\ A'&20 & & \\ \hline & 100 & & 1000 \end{array} \quad\Rightarrow\quad \begin{array}{c|cc|c} & B & B' &\\ \hline A & 80&200 & 280\\ A'& 20 &700& 720 \\ \hline & 100 &900 &1000 \end{array} \end{gathered} \] Die geschätzten Wahrscheinlichkeiten betragen dann \[ \begin{gathered} \begin{array}{c|cc|c} & B & B' &\\ \hline A & 0.08& 0.20 & 0.28\\ A'&0.02 & 0.70& 0.72 \\ \hline & 0.10 & 0.90 &1.00 \end{array} \end{gathered} \] (a) Der Anteil der Verkehrsunfälle mit Todesfolge an den Hochgeschwindigkeitsunfällen ist: \[ \begin{gathered} P(A|B)=\dfrac{P(A\cap B)}{P(B)}=\dfrac{0.08}{0.1}=0.8\,. \end{gathered} \] (b) Der Anteil der Hochgeschwindigkeitsunfälle an Verkehrsunfällen mit Todesfolge beträgt: \[ \begin{gathered} P(B|A)=\dfrac{P(A\cap B)}{P(A)}=\dfrac{0.08}{0.28}=0.2857\,. \end{gathered} \] (c) Weil \(P(A|B)>P(A)=0.28\) und \(P(B|A)>P(B)=0.1\) besteht eine positive Kopplung. Die beiden Ereignisse begünstigen einander.

Diese Ergebnisse legen es nahe zu vermuten, dass hohe Geschwindigkeit eine Ursache für den tödlichen Verlauf eines Unfalls ist. Dieser Schluss ist aber nicht zwingend. Es könnte auch sein, dass bestimmte Charaktermerkmale des Lenkers sowohl die hohe Geschwindigkeit als auch die Tödlichkeit des Unfalls verursachen. □

Es ist wichtig, sich immer vor Augen zu halten, dass Kopplung von zwei Ereignissen kein Hinweis auf eine kausale Beziehung zwischen den Ereignissen sein muss. Es kommt sehr häufig vor, dass eine Schichtung der Grundgesamtheit die Ursache für eine Scheinkopplung von Ereignissen ist.

Keine Kopplung liegt hingegen vor, wenn \(P(A|B)=P(A)\) bzw. \(P(B|A)=P(B)\). In diesem Fall nennt man die beiden Ereignisse unabhängig. Das hat eine wichtige Konsequenz: \[ \begin{aligned} P(A|B)=P(A) & \implies \frac{P(A \cap B)}{P(B)}=P(A) \\ & \implies P(A \cap B)=P(A)P(B). \end{aligned} \]

Satz 5.34 (Stochastische Unabhängigkeit) Zwei Ereignisse \(A\) und \(B\) sind stochastisch unabhängig, wenn \[ \begin{gathered} P(A\cap B)=P(A)P(B). \end{gathered} \tag{5.17}\] Andernfalls sind sie stochastisch abhängig oder gekoppelt.

Hat man es mit mehr als zwei Ereignissen \(A_1,A_2,\ldots,A_n\) zu tun, so bedeutet Unabhängigkeit der Ereignisse, dass für alle Auswahlen \(i_1<i_2<\ldots< i_k\) die Gleichung \[ \begin{gathered} P(A_{i_1}\cap A_{i_2}\cap\ldots\cap A_{i_k})= P(A_{i_1})P(A_{i_2})\cdots P(A_{i_k}) \end{gathered} \tag{5.18}\] richtig ist.

Es gibt zahlreiche Anwendungsfälle, bei denen man von vornherein weiß, dass gewisse Ereignisse unabhängig sind. Diese Information kann dann zur Bestimmung von Wahrscheinlichkeiten herangezogen werden. Tatsächlich werden viele Fragestellungen durch die Annahme der Unabhängigkeit erheblich vereinfacht.

Musteraufgabe 5.35 (Verfahrenstechnik) Ein technisches System bestehe aus 3 Teilen, die unabhängig voneinander ausfallen können. Die Ausfallwahrscheinlichkeiten der einzelnen Teile betragen 0.2, 0.3 und 0.1. Es sei \(X\) die Anzahl der ausfallenden Teile. Bestimmen Sie die Wahrscheinlichkeitsfunktion der Zufallsgröße \(X\), d.h. \[ \begin{gathered} P(X=0),\quad P(X=1), \quad P(X=2),\quad P(X=3). \end{gathered} \]

Lösung: Es bezeichnen \(A,\,B,\, C\) die Ereignisse, dass jeweils einer der drei Teile ausfällt. Gegeben sind die Wahrscheinlichkeiten \(P(A)=0.2\), \(P(B)=0.3\) und \(P(C)=0.1\).

Unter Berücksichtigung der Unabhängigkeit der Ereignisse \(A,B,C\) und des Additionsgesetzes erhalten wir: \[ \begin{gathered} \small \begin{array}{l l } P(X=0) & = P(A'\cap B'\cap C')=P(A')P(B')P(C')\\[4pt] & = 0.8 \cdot 0.7 \cdot 0.9 = 0.504,\\[7pt] P(X=1) & = P(A\cap B' \cap C')+ P(A'\cap B \cap C')+ P(A'\cap B' \cap C)\\[4pt] & = P(A)P(B')P(C')+P(A')P(B)P(C')+P(A')P(B')P(C)\\[4pt] & =0.2\cdot 0.7 \cdot 0.9 + 0.8\cdot 0.3 \cdot 0.9 + 0.8\cdot 0.7\cdot 0.1 = 0.398,\\[7pt] P(X=2) & = P(A\cap B\cap C')+ P(A\cap B'\cap C)+ P(A'\cap B \cap C)\\[4pt] & = P(A)P(B)P(C')+P(A)P(B')P(C)+P(A')P(B)P(C)\\[4pt] & = 0.2\cdot 0.3 \cdot 0.9 + 0.2 \cdot 0.7 \cdot 0.1 + 0.8 \cdot 0.3 \cdot 0.1 =0.092,\\[7pt] P(X=3) & = P(A \cap B\cap C)=P(A)P(B)P(C)\\[4pt] &= 0.2 \cdot 0.3 \cdot 0.1 = 0.006\,. \end{array} \end{gathered} \]

Daher lautet die Wahrscheinlichkeitsfunktion der Zufallsgröße \(X\) in Tabellenform: \[ \begin{gathered} \begin{array}{c|cccc} k & 0 & 1 & 2 & 3\\ \hline P(X=k) & 0.504 & 0.398 & 0.092 & 0.006 \end{array} \end{gathered} \] □

Das Konzept der Unabhängigkeit lässt sich auch auf Zufallsgrößen übertragen, denn Aussagen über Zufallsgrößen wie \(\{X>b\}\) oder \(\{a<X\le b\}\) sind ja zufällige Ereignisse.

Definition 5.36 Zwei Zufallsgrößen \(X\) und \(Y\) heißen stochastisch unabhängig, wenn Aussagen über die Zufallsgrößen stochastisch unabhängige Ereignisse sind.

Bemerkung 5.37 Wenn \(X\) und \(Y\) unabhängig sind, dann sind das auch die Ereignisse \(\{X\le a\}\) und \(\{Y\le b\}\). Daher ist \[ \begin{gathered} P(\{X\le a\}\cap \{Y\le b\})=P(X\le a)\cdot P(Y\le b). \end{gathered} \] Da Ausdrücke wie auf der linken Seite dieser Gleichung in Anwendungen (z.B. in der Statistik) sehr häufig vorkommen, hat sich eine vereinfachte Komma-Schreibweise eingebürgert: \[ \begin{gathered} P(\{X\le a\}\cap \{Y\le b\})=P(X\le a, Y\le b). \end{gathered} \]

Musteraufgabe 5.38 (Ein Callcenter) Ein Unternehmen betreibt ein Callcenter zur effizienten Bearbeitung von Kundenanfragen. Es ist bekannt, dass die Dauer \(T\) (in Minuten) eines Kundengesprächs eine stetige Zufallsgröße ist mit Verteilungsfunktion \(P(T\le t)=1-e^{-t/10}\).

Drei Kunden rufen zur selben Zeit an und erhalten sofort eine Sachbearbeiterin. Ihre Gespräche dauern \(T_1, T_2\) und \(T_3\) Minuten, wobei diese Zufallsgrößen stochastisch unabhängig sind.

Wie groß ist die Wahrscheinlichkeit, dass das längste der drei Gespräche länger als 20 Minuten dauert.

Lösung: Es sei \(M=\max(T_1,T_2,T_3)\), wobei \(T_1,T_2\) und \(T_3\) unabhängig sind. Wir betrachten zuerst das Ereignis \(\{M\le h\}\). Dieser Ereignis kann nur eintreten, wenn jedes \(T_i\le h\) ist: \[ \begin{gathered} \{M\le h\} \Leftrightarrow \{T_1\le h\}\cap \{T_2\le h\} \cap \{T_3\le h\}, \end{gathered} \] denn wäre nur ein \(T_i>h\), könnte \(M\) nicht mehr \(\le h\) sein. Äquivalente Ereignisse haben gleiche Wahrscheinlichkeit, daher: \[ \begin{aligned} P(M\le h)&=P(T_1\le h,T_2\le h,T_3\le h)\\[4pt] &=P(T_1\le h)\cdot P(T_2\le h)\cdot P(T_3\le h)\quad\text{(Unabhängigkeit)}\\[4pt] &=(1-e^{-h/10})^3. \end{aligned} \] Wir suchen \[ \begin{aligned} P(M>20)&=1-P(M\le 20)=1-(1-e^{-20/10})^3=0.3535\,. \end{aligned} \] Dies ist eine vergleichsweise hohe Wahrscheinlichkeit, denn dass ein Gespräch, etwa das erste, länger als 20 Minuten dauert, ist bloß: \[ \begin{gathered} P(T_1>20)=e^{-20/10}=0.1353\,. \end{gathered} \] □

5.3 Erwartungswert und Varianz

5.3.1 Der Begriff des Erwartungswerts

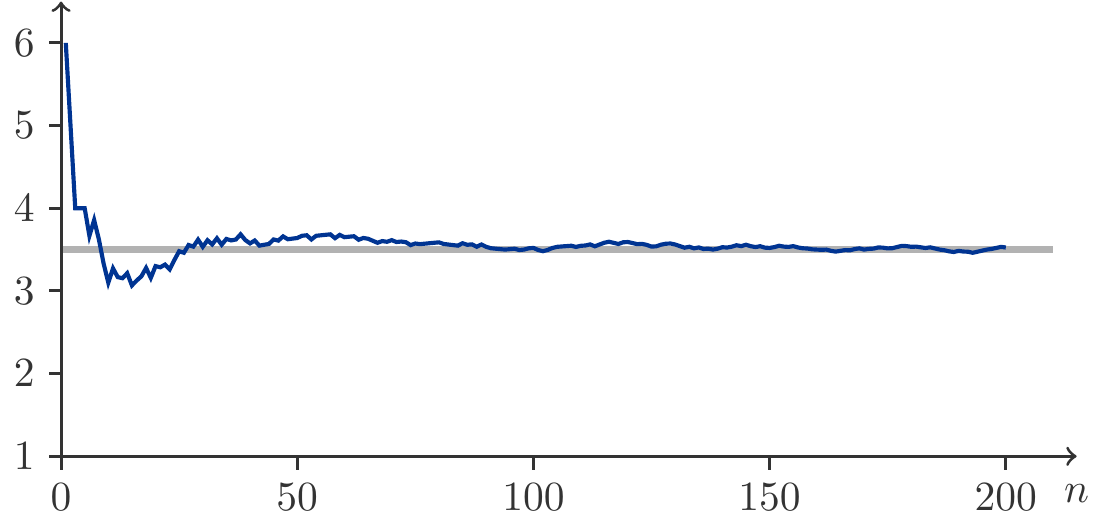
Es sei \(X\) eine Zufallsgröße. Wenn man das zugrunde liegende Zufallsexperiment häufig wiederholt und die dabei entstehenden Werte der Zufallsgröße \(X\) sammelt, dann entsteht eine Datenliste \(x_1,x_2,\ldots\). Wir können nun die Mittelwerte \[ \begin{aligned} \bar{x}_1 &=\frac{x_1}{1},\;\bar{x}_2=\frac{x_1+x_2}{2},\;\bar{x}_3=\frac{x_1+x_2+x_3}{3}, \\ \bar{x}_4 &=\frac{x_1+x_2+x_3+x_4}{4}, \ldots \end{aligned} \tag{5.19}\] berechnen und den Verlauf der Mittelwerte mit wachsender Anzahl der Daten studieren. Bei vielen Zufallsgrößen stellt man fest, dass diese Mittelwerte sich im Laufe der Zeit einem festen Wert nähern (sofern die Wiederholungen voneinander unabhängig sind und unter identischen Bedingungen erfolgen). Dieser Grenzwert ist der langfristige Durchschnitt der zufälligen Werte der Zufallsgröße und wird als Erwartungswert der Zufallsgröße bezeichnet.

Bemerkung 5.39 (Existenz von Erwartungswerten) Es ist keineswegs so, dass für jede Zufallsgröße die Mittelwerte der Datenlisten konvergieren. Wenn das nicht der Fall ist, dann macht der Begriff des Erwartungswerts für so eine Zufallsgröße keinen Sinn. Man sagt dann, dass die Zufallsgröße keinen Erwartungswert besitzt. Wir werden aber im folgenden solche Zufallsgrößen nicht in Betracht ziehen.

Abbildung 5.9: Die Mittelwerte (5.19) aus 200 Würfen eines Würfels.

Unsere Erklärung des Begriffs des Erwartungswerts ist sehr ähnlich zu unserer Erklärung des Begriffs der Wahrscheinlichkeit. Daraus ergibt sich auch ein erster fundamentaler Zusammenhang zwischen Wahrscheinlichkeiten und Erwartungswerten.

Es sei \(A\) ein Ereignis und \(X_A\) sei folgende Zufallsgröße: \[ \begin{gathered} X_A(\omega)=\left\{\begin{array}{ll} 1 &\text{wenn $\omega\in A$},\\ 0 &\text{wenn $\omega\not\in A$} \end{array}\right. \end{gathered} \] Die Zufallsgröße \(X_A\) zeigt das Eintreten des Ereignisses \(A\) an. Man nennt sie deshalb die Indikatorgröße des Ereignisses \(A\).

Um den Erwartungswert einer Indikatorgröße \(X_A\) zu bestimmen, muss man sich die Mittelwerte von Datenlisten ansehen, die durch eine Indikatorgröße entstehen. Es ist leicht zu sehen, dass diese Mittelwerte identisch sind mit den relativen Häufigkeiten, mit denen das Ereignis \(A\) in einer Reihe von Wiederholungen des Zufallsexperiments auftritt. Daher muss auch der Grenzwert der Mittelwerte von \(X_A\) mit dem Grenzwert der relativen Häufigkeiten von \(A\) übereinstimmen. Das bedeutet \(E(X_A)=P(A)\).

Eine weitere fundamentale Eigenschaft des Erwartungswerts von Zufallsgrößen ist eine Rechenregel, die man als Linearität bezeichnet.

Sind \(X\) und \(Y\) zwei Zufallsgrößen und \(a,b\in\mathbb R\) zwei beliebige reelle Zahlen. Dann können wir eine weitere Zufallsgröße \(Z=aX+bY\) bilden. Es ist offensichtlich, dass für die Mittelwerte \(\overline{x}, \overline{y}\) und \(\overline{z}\) von Datenlisten dieser Zufallsgrößen die Gleichung \(\overline{z}=a\overline{x}+b\overline{y}\) gilt. Daraus folgt \(E(Z)=aE(X)+bE(Y)\).

Auf ganz ähnliche Weise begründet man, dass eine Zufallsgröße, deren Werte nichtnegativ sind, auch einen nichtnegativen Erwartungswert haben muss: \(X\ge 0 \implies E(X)\ge 0\).

Wir fassen zusammen:

Satz 5.40 Der Erwartungswert von Zufallsgrößen hat folgende Eigenschaften:

(a) Der Erwartungswert einer Indikatorgröße ist identisch mit der Wahrscheinlichkeit des zugrundeliegenden Ereignisses: \[ \begin{gathered} E(X_A)=P(A). \end{gathered} \]

(b) Der Erwartungswert einer Linearkombination von Zufallsgrößen ist identisch mit der entsprechenden Linearkombination der Erwartungswerte: \[ \begin{gathered} E(aX+bY)=aE(X)+bE(Y). \end{gathered} \]

(c) Der Erwartungswert einer nichtnegativen Zufallsgröße ist nichtnegativ: \[ \begin{gathered} X\ge 0 \implies E(X)\ge 0. \end{gathered} \]

Musteraufgabe 5.41 (Kostenmodell) Ein Produktionsunternehmen arbeitet mit monatlichen Fixkosten von 1000 GE und variablen Stückkosten von 5 GE. Die monatliche Produktion ist eine Zufallsgröße mit dem Erwartungswert von 300 Stück. Man finde den Erwartungswert der monatlichen Kosten.

Lösung: Bezeichnet \(X\) die monatliche Produktion und \(Y\) die monatlichen Kosten, dann gilt \(Y=1000+5X\). Folglich ist \[ \begin{gathered} E(Y)=E(1000+5X)=1000+5E(X)=1000+5\cdot 300=2500. \end{gathered} \] □

5.3.2 Berechnung von Erwartungswerten

In den folgenden Beispielen berechnen wir Erwartungswerte von Zufallsgrößen, die endlich viele verschiedene Werte annehmen können.

Sei \(X\) beispielsweise eine Zufallsgröße mit zwei möglichen Werten \(a\) und \(b\) und sei \(A=\{X=a\}\) und \(B=\{X=b\}\). Dann kann man die Zufallsgröße \(X\) als Linearkombination von Indikatorgrößen darstellen: \[ \begin{gathered} X=aX_A+bX_B. \end{gathered} \] Es ist sehr wichtig, die Gültigkeit dieser Gleichung vollständig zu verstehen: Wenn \(\{X=a\}\) zutrifft, dann ist \(X_A=1\) und \(X_B=0\). Daher hat dann die Linearkombination auf der rechten Seite den Wert \(a\) und die Gleichung ist richtig. Ähnlich verhält es sich, wenn \(\{X=b\}\) zutrifft.

Aus der Gültigkeit der Gleichung \(X=aX_A+bX_B\) folgt dann nach den Rechenregeln für den Erwartungswert, dass \[ \begin{gathered} E(X)=aE(X_A)+bE(X_B)=aP(A)+bP(B). \end{gathered} \] Diese Beobachtung lässt sich verallgemeinern auf Zufallsgrößen, die endlich viele Werte annehmen können.

Satz 5.42 Es sei \(X\) eine Zufallsgröße, die die Werte \(a_1, a_2,\ldots,a_n\) mit den Wahrscheinlichkeiten \(P(X=a_k)=p_k\) annimmt. Dann beträgt \(E(X)\): \[ \begin{gathered} E(X)=a_1p_1+a_2p_2+\cdots+a_np_n. \end{gathered} \tag{5.20}\] Mit anderen Worten: \(E(X)\) ist ein gewogenes Mittel der Werte \(a_1,\ldots,a_n\) von \(X\), gewichtet mit den Wahrscheinlichkeiten \(p_1,\ldots,p_n\).

Musteraufgabe 5.43 (Würfelwurf) (a) Was ist die erwartete Augenzahl beim Werfen eines Würfels?

(b) Man finde den Erwartungswert der Summe der Augenzahlen beim zweimaligen Werfen eines Würfels.

Lösung: Die Augenzahl ist eine Zufallsgröße \(X\) mit Werten \(1,2,\ldots,6\), die jeweils mit Wahrscheinlichkeit \(1/6\) gewürfelt werden.

(a) Wir wenden (5.20) an: \[ \begin{aligned} E(X)&=1\cdot P(X=1)+2\cdot P(X=2)+\cdots+6\cdot P(X=6)\\ &=\frac{1}{6}(1+2+\cdots+6)=3.5\,. \end{aligned} \] Dies ist eine formale Bestätigung des Experiments aus der Abbildung 5.9.

(b) Es sei \(X\) die Augenzahl beim ersten Wurf und \(Y\) die Augenzahl beim zweiten Wurf. Dann gilt (Satz 5.40 (b)): \[ \begin{gathered} E(X+Y)=E(X)+E(Y)=3.5+3.5=7 \end{gathered} \] □

Ein Glücksspiel heißt fair, wenn der Erwartungswert des Gewinns \(G\) mit dem Einsatz übereinstimmt.

Musteraufgabe 5.44 (Glückspiel) Beim Lotto 6 aus 45 beträgt der Einsatz für eine Wette 10 GE. Wie hoch muss der Gewinn bei einem Haupttreffer sein, damit es sich um ein faires Glücksspiel handelt?

Lösung: Es sei \(A\) das Ereignis, einen Haupttreffer zu erzielen und \(G\) der erzielte Gewinn. Damit es sich um ein faires Glücksspiel handelt, muss die Gleichung \[ \begin{aligned} \text{Einsatz }&=E(G)=E(\text{Gewinnhöhe}\cdot X_A)=\\ &= \text{Gewinnhöhe}\cdot E(X_A)= \text{Gewinnhöhe}\cdot P(A) \end{aligned} \] gelten. Dabei haben wir Satz 5.40 (a) und (b) angewendet. Es folgt: \[ \begin{gathered} \frac{\text{Einsatz}}{P(A)}=\text{Gewinnhöhe} \end{gathered} \] Die Wahrscheinlichkeit \(P(A)\) für den Haupttreffer haben wir schon in Musteraufgabe 5.12 berechnet. Daher muss die Gewinnhöhe für eine faire Wette sein: \[ \begin{gathered} \frac{10}{P(A)}=10\cdot\frac{45\cdot 44\cdots 43\cdot 40}{ 6\cdot 5\cdots 2\cdot 1}=81\,450\,600. \end{gathered} \]

Musteraufgabe 5.45 (Finanzmathematik) Ein Wertpapier mit dem Anfangswert \(300\) steigt mit der Wahrscheinlichkeit 0.2 innerhalb eines Jahres um 5 Prozent, oder aber es fällt um 5 Prozent. Man finde den Erwartungswert des Werts dieser Anlage nach einem Jahr.

Lösung: Es bezeichne \(W\) den Wert des Wertpapiers nach einem Jahr und es sei \(A\) das Ereignis, dass das Wertpapier um 5 Prozent steigt. Wir behelfen uns wieder mit Indikatoren. Dann ist \[ \begin{gathered} W=300\cdot 1.05 \cdot X_A+ 300\cdot 0.95 \cdot X_{A'}=315 X_A+285 X_{A'}. \end{gathered} \] Daraus folgt wegen Satz 5.40: \[ \begin{aligned} E(W)&= 315 E(X_A)+285 E(X_{A'})=315 P(A)+285P(A')\\ &=315\cdot 0.2+285\cdot 0.8= 291. \end{aligned} \]

Erwartungswerte stetiger Zufallsgrößen

Diese werden durch Integrale definiert. Genauer, besitzt die stetige Zufallsgröße \(X\) die Dichte \(f(x)\), dann ist ihr Erwartungswert: \[ \begin{gathered} E(X)=\int_{-\infty}^\infty xf(x)\,\mathrm{d}x. \end{gathered} \tag{5.21}\] Die Berechnung dieser Integrale erfordert in der Regel fortgeschrittene Methoden der Analysis, sodass wir hier nicht weiter darauf eingehen. Der Vollständigkeit halber führen wir zwei Spezialfälle an, die uns in Anwendungen schon begegnet sind (siehe Beispiel 5.24 und Beispiel 5.26):

Satz 5.46 Ist \(T\) exponentialverteilt mit Verteilungsfunktion \(F(t)=1-e^{-\lambda t}, t\ge 0\), dann ist \(E(T)=1/\lambda\).

Ist \(X\) logistisch verteilt mit Verteilungsfunktion \(F(x)=\dfrac{1}{1+e^{-(x-\mu)/s}}, X\in\mathbb R\), dann ist \(E(X)=\mu\).

Wir sehen uns nun eine interessante Aufgabenstellung aus der Versicherungsmathematik an.

Eine Erlebensversicherung besteht in der Zusage, nach Ablauf eines Zeitraums von \(t\) Jahren ein Kapital \(K\) auszuzahlen, falls der Versicherungsnehmer zu diesem Zeitpunkt noch lebt. Bezeichnet \(A\) das Ereignis, dass der Versicherungsnehmer die \(t\) Jahre der Wartezeit überlebt, so beträgt die Auszahlung offenbar \(K\cdot X_A\). Der Barwert der Auszahlung zum Zeitpunkt des Abschlusses der Versicherung ist \(B=Kd^tX_A\), wenn \(d\) den Abzinsungsfaktor bezeichnet.

Unter dem Risiko der Versicherung versteht man den Erwartungswert \(R=E(B)\) des Barwertes der Auszahlung. Ist \(q\) die Sterbewahrscheinlichkeit des Versicherten im Lauf eines Jahres, so ist (sehr vereinfacht) \(P(A)=(1-q)^t\) und daher beträgt das Risiko der Versicherung \[ \begin{gathered} R=E(B)=Kd^t(1-q)^t. \end{gathered} \] Das Versicherungsprinzip besagt, dass die Prämie eines Versicherungsvertrags, dh. der vom Versicherungsnehmer zu zahlende Preis, mit dem Risiko der Versicherung übereinstimmen muss. In der Praxis enthält eine Versicherungsprämie auch noch Verwaltungsgebühren und ist daher größer als eine reine Risikoprämie.

Musteraufgabe 5.47 (Versicherungen) Berechnen Sie die Risikoprämie für einen 40–jährigen Mann und eine 40–jährige Frau, die eine Erlebensversicherung über ein Kapital von 100 000 GE, auszuzahlen nach 10 Jahren, abschließen wollen. Der versicherungsrechtlich verbindliche Rechungszinssatz beträgt 3 %.

Die Sterbewahrscheinlichkeiten betragen für 40-jährige Männer \(q_m=0.003\) und für 40-jährige Frauen \(q_w=0.0015\).

Wie hoch ist die Rendite eines überlebenden Versicherungsnehmers aus einem solchen Versicherungsvertrags?

Lösung: Für Männer beträgt die Risikoprämie \[ \begin{gathered} R_m=100000 \left( \frac{1}{1.03}\right)^{10} (1-0.003)^{10}=72207. \end{gathered} \] Die jährliche Rendite \(r\) ergibt sich aus \(K_{10}=K_0(1+r)^{10}=R_m(1+r)^{10}\) und beträgt \[ \begin{gathered} \left(\frac{100000}{72207}\right)^{1/10}-1=0.0331\,. \end{gathered} \] Für Frauen beträgt die Risikoprämie \[ \begin{gathered} R_m=100000 \left( \frac{1}{1.03}\right)^{10} (1-0.0015)^{10}=73301. \end{gathered} \] Die Rendite beträgt \[ \begin{gathered} \left(\frac{100000}{73301}\right)^{1/10}-1=0.0315\,. \end{gathered} \] □

5.3.3 Der Multiplikationssatz für Erwartungswerte

Der Erwartungswert besitzt eine bemerkenswerte Multiplikationseigenschaft, wenn er auf Produkte von unabhängigen Zufallsgrößen angewendet wird.

Die Unabhängigkeit von Ereignissen lässt sich, wie wir wissen, mathematisch als Multiplikationseigenschaft von Wahrscheinlichkeiten formalisieren. Etwas ähnliches gilt für Zufallsgrößen und ihren Erwartungswert.

Man kann das direkt an Indikatorgrößen sehen. Sind \(A\) und \(B\) zwei Ereignisse, so gilt offenbar \(X_{A\cap B}=X_AX_B\), denn das Ereignis \(A\cap B\) tritt nur ein, wenn beide Ereignisse \(A\) und \(B\) gleichzeitig eintreten. Dann ist aber \(X_A=1\) und \(X_B=1\) und deshalb \(X_AX_B=1\). Daraus folgt \(E(X_AX_B)=E(X_{A\cap B})=P(A\cap B)\). Wir erhalten so \[ \begin{gathered} E(X_AX_B)=E(X_A)E(X_B)\quad \Leftrightarrow\quad P(A\cap B)=P(A)P(B). \end{gathered} \] Also sind die beiden Ereignisse \(A\) und \(B\) genau dann unabhängig, wenn für ihre Erwartungswerte die Formel \[ \begin{gathered} E(X_AX_B)=E(X_A)E(X_B). \end{gathered} \] richtig ist.

Allgemein gilt die folgende Aussage.

Satz 5.48 Es seien \(X\) und \(Y\) zwei Zufallsgrößen, die einen Erwartungswert besitzen. Sind \(X\) und \(Y\) unabhängig, dann gilt \[ \begin{gathered} E(XY)=E(X)E(Y). \end{gathered} \tag{5.22}\]

5.3.4 Die Varianz von Zufallsgrößen

Es sei \(X\) eine Zufallsgröße mit dem Erwartungswert \(E(X)=\mu\).

Der Erwartungswert einer Zufallsgröße liefert uns Information über die langfristigen Durchschnittswerte der Zufallsgröße. Der Erwartungswert gibt uns aber keine Auskunft darüber, wie stark die Werte der Zufallsgröße um \(\mu\) streuen. Um uns über die Streuung der Werte einer Zufallsgröße ein Bild zu machen, interessieren wir uns für die Abweichungen \(X-\mu\) der Zufallsgröße von ihrem Erwartungswert.

Definition 5.49 Es sei \(X\) eine Zufallsgröße und \(\mu\) ihr Erwartungswert. Der Erwartungswert der Zufallsgröße \((X-\mu)^2\) heißt Varianz der Zufallsgröße: \[ \begin{gathered} \sigma^2=V(X)=E (X-\mu)^2. \end{gathered} \] Die Wurzel \(\sigma=\sqrt{V(X)}\) wird als Standardabweichung von \(X\) bezeichnet.

Für die Berechnung von Varianzen wird eine vereinfachte Formel verwendet, die den Rechenaufwand vermindert.

Satz 5.50 (Verschiebungssatz) Es sei \(X\) eine Zufallsgröße mit dem Erwartungswert \(E(X)=\mu\) und der Varianz \(V(X)\). Dann gilt \[ \begin{gathered} V(X)=E(X^2)-\mu^2. \end{gathered} \]

Begründung: Dies folgt ganz einfach aus der Definition 5.49. Wenn wir das Quadrat ausführen: \[ \begin{aligned} V(X)&=E(X^2-2\mu X+\mu^2)=E(X^2)-2\mu E(X)+\mu^2\\[5pt] &=E(X^2)-2\mu^2+\mu^2=E(X^2)-\mu^2. \end{aligned} \] □

Musteraufgabe 5.51 Berechnen Sie die Varianz der Augenzahl beim Werfen eines Würfels.

Lösung: Wir kennen schon \(E(X)=3.5\). Nun berechnen wir \(E(X^2)\): \[ \begin{gathered} E(X^2)=\frac{1}{6}\left(1^2+2^2+3^2+4^2+5^2+6^2\right)=\frac{91}{6}=15.1667. \end{gathered} \] Daraus folgt dann (unter Verwendung von Satz 5.50) \[ \begin{gathered} V(X)=E(X^2)-\mu^2=\frac{91}{6}-\left(\frac{7}{2}\right)^2=\frac{35}{12}\simeq 2.9167. \end{gathered} \] □

In der nächsten Aufgabe greifen wir nochmals das verfahrenstechnische Problem aus Musteraufgabe 5.35 auf.

Musteraufgabe 5.52 Eine Zufallsgröße \(X\) besitzt die Wahrscheinlichkeitsfunktion: \[ \begin{gathered} \begin{array}{c|cccc} k & 0 & 1 & 2 & 3\\ \hline P(X=k) & 0.504 & 0.398 & 0.092 & 0.006 \end{array} \end{gathered} \] Berechnen Sie \(E(X)\) und \(V(X)\).

Lösung: Wir berechnen zunächst \(\mu=E(X)\) und \(E(X^2)\): \[ \begin{aligned} \mu&=0\cdot 0.504+1\cdot 0.398+2\cdot 0.092+3\cdot 0.006=0.6,\\[4pt] E(X^2)&=0^2\cdot 0.504+1^2\cdot 0.398+2^2\cdot 0.092+3^2\cdot 0.006=0.82\,. \end{aligned} \] Daraus folgt dann \[ \begin{gathered} V(X)=E(X^2)-\mu^2=0.82-0.6^2=0.46\,. \end{gathered} \] □

Bemerkung 5.53 (Interpretation der Varianz) Wie man schon aus der Definition der Varianz ablesen kann, enthält die Varianz \(V(X)\) einer Zufallsgröße \(X\) Information darüber, wie stark die Zufallsgröße \(X\) um ihren Erwartungswert \(E(X)\) schwanken kann. Diese Information kann man mathematisch ziemlich genau angeben.

Es bezeichne \(\sigma=\sqrt{V(X)}\) die Standardabweichung der Zufallsgröße \(X\). Man kann nun die Frage stellen, wie groß die Abweichungen \(X-E(X)\) sein können. Diese Frage kann freilich nur dann präzise beantwortet werden, wenn die Verteilung von \(X\) bekannt ist.

Eine in überraschend vielen Anwendungen auftretende Wahrscheinlichkeitsverteilung ist die Normalverteilung (siehe Kapitel 5.4). Für normalverteilte Zufallsgrößen gilt: \[ \begin{gathered} P(|X-E(X)|\le \sigma)\approx 0.66, \quad P(|X-E(X)|\le 2\sigma)\approx 0.95 \end{gathered} \] Die Standardabweichung kann also für die Bildung von Faustregeln benutzt werden, mit denen man die Schwankungsbereiche von Zufallsgrößen ungefähr angibt: Im Intervall \((E(X)-\sigma,E(X)+\sigma)\) liegen 66 Prozent beobachteten Werte von \(X\), usw.

Die oben angegebenen Regeln beruhen allerdings auf den Eigenschaften der Normalverteilung. In ungünstigen Fällen kann es passieren, dass die Wahrscheinlichkeiten der Schwankungsintervalle wesentlich kleiner sind als oben angegeben.

Wir wenden uns nun den Rechenregeln für Varianzen zu. Als erstes sehen wir uns an, wie sich die Varianz ändert, wenn wir eine Zufallsgröße einer linearen Transformation unterwerfen.

Satz 5.54 Es sei \(X\) eine Zufallsgröße mit der Varianz \(V(X)\). Dann gilt \[ \begin{gathered} V(aX+b)=a^2V(X) \quad \text{für $a,b \in \mathbb R$}. \end{gathered} \]

Begründung: Aus der Definition 5.49 der Varianz ergibt sich: \[ \begin{aligned} V(aX+b)&=E(aX+b-E(aX+b))^2=E(aX-aE(X))^2\\ &=a^2E(X-E(X))^2=a^2V(X). \end{aligned} \] So nebenbei ergibt sich daraus auch die fast selbstverständliche Tatsache, dass die Varianz einer Konstanten Null ist, also \(V(b)=0\). □

Musteraufgabe 5.55 (Lineares Kostenmodel) Ein Produktionsunternehmen arbeitet mit monatlichen Fixkosten von 1000 GE und variablen Stückkosten von 5 GE. Die monatliche Produktion ist eine Zufallsgröße mit der Standardabweichung von 20 Stück. Man finde die Varianz und die Standardabweichung der monatlichen Kosten.

Lösung: Bezeichnet \(X\) die monatliche Produktion und \(Y\) die monatlichen Kosten, dann gilt \(Y=1000+5X\). Folglich ist (weil \(V(X)=20^2=400\)): \[ \begin{gathered} V(Y)=V(1000+5X)=25V(X)=25\cdot 400 =10\,000. \end{gathered} \] Die Standardabweichung \(\sqrt{V(Y)}\) beträgt 100. □

Es ist nicht zu erwarten und auch nicht zutreffend, dass die Varianz einer Summe von Zufallsgrößen mit der Summe der einzelnen Varianzen übereinstimmt. Umso bemerkenswerter ist es, dass für unabhängige Zufallsgrößen sehr wohl ein solches Additionsgesetz für Varianzen gilt.

Satz 5.56 Sind \(X\) und \(Y\) unabhängige Zufallsgrößen, dann gilt \[ \begin{aligned} V(X+Y)&=V(X)+V(Y). \end{aligned} \]

Begründung: Wir beginnen zu rechnen und verwenden dabei erneut Definition 5.49: \[ \begin{gathered} \begin{array}{rcl} V(X+Y) & = & E(X+Y - E(X+Y))^2 \\ & = & E(X-E(X) +Y-E(Y))^2\\ & = & E(X-E(X))^2 +2E\left[(X-E(X))(Y-E(Y))\right]\\ & & +E(Y-E(Y))^2. \end{array} \end{gathered} \] Für den Mittelteil folgt aber aus der Multiplikationseigenschaft (5.22), dass \[ \begin{gathered} E\left[(X-E(X))(Y-E(Y))\right]=E(X-E(X))E(Y-E(Y))=0, \end{gathered} \] denn \(E(X-E(X))=E(X)-E(E(X))=E(X)-E(X)=0\). □

Interessanterweise gilt das Additionsgesetz auch dann, wenn wir Differenzen von unabhängigen Zufallsgrößen betrachten, denn \[ \begin{aligned} V(X-Y) & = V(X)+V\left((-1)Y\right)\\ & = V(X)+(-1)^2V(Y)=V(X)+V(Y). \end{aligned} \]

5.3.5 Die Rendite eines Portfolios

Das Additionsgesetz für Varianzen hat eine wichtige Anwendung in der Finanzmathematik. Es hat nämlich zur Folge, dass bei der Bildung von Portfolios von Wertpapieren Diversifikation zur Verringerung des Risikos führt.

Unter der Rendite \(R\) eines Wertpapiers versteht man den relativen Wertzuwachs in einer Periode. Wenn zu Beginn der Wert des Papiers \(V_0\) GE war und am Ende der Periode der Wert \(V_1\) GE beträgt, dann ist die mit dieser Anlage in einer Periode erzielte Rendite \[ \begin{gathered} R=\frac{V_1-V_0}{V_0}. \end{gathered} \] Ein Portfolio ist eine Entscheidung, wie zur Verfügung stehendes Kapital in zwei oder mehr Wertpapiere investiert wird. Angenommen, wir bilden ein Portfolio aus drei Wertpapieren \(A, B\) und \(C\). Am Beginn der Periode treffen wir die Entscheidung, die Beträge \(A_0,\;B_0,\;C_0\) in diese Papiere zu investieren. Wenn am Ende der Periode diese Investments Werte von \(A_1, B_1\) und \(C_1\) haben, dann ist die gemeinsame Rendite \(R\) des so gebildeten Portfolios die relative Wertänderung der investierten Summe: \[ \begin{aligned} R&=\dfrac{A_1+B_1+C_1-(A_0+B_0+C_0)}{A_0+B_0+C_0}. \end{aligned} \tag{5.23}\] Wir setzen: \[ \begin{gathered} R_A=\frac{A_1-A_0}{A_0},\quad R_B=\frac{B_1-B_0}{B_0},\quad R_C=\frac{C_1-C_0}{C_0}, \end{gathered} \] das sind die Renditen der drei Wertpapiere. Wir können nun die gemeinsame Rendite \(R\) ausdrücken mit Hilfe der Renditen \(R_A, R_B\) und \(R_C\): \[ \begin{gathered} \begin{array}{rcl} R & = & \displaystyle \frac{A_1-A_0}{A_0+B_0+C_0} + \frac{B_1-B_0}{A_0+B_0+C_0} + \frac{C_1-C_0}{A_0+B_0+C_0}\\[4pt] & = & \displaystyle \frac{A_0}{A_0+B_0+C_0} \cdot \frac{A_1-A_0}{A_0} + \frac{B_0}{A_0+B_0+C_0} \cdot \frac{B_1-B_0}{B_0}+\\[4pt] & & \displaystyle \frac{C_0}{A_0+B_0+C_0} \cdot \frac{C_1-C_0}{C_0}\\[4pt] & = & \displaystyle \frac{A_0}{A_0+B_0+C_0} \cdot R_A + \frac{B_0}{A_0+B_0+C_0} \cdot R_B +\\[4pt] & & \displaystyle \frac{C_0}{A_0+B_0+C_0} \cdot R_C. \end{array} \end{gathered} \] Die gemeinsame Rendite ist also das gewichtete Mittel der einzelnen Renditen, wobei als Gewichte die Kapitalanteile (Prozentsätze) der einzelnen Wertpapiere zu verwenden sind: \[ \begin{gathered} \alpha=\frac{A_0}{A_0+B_0+C_0},\quad \beta=\frac{B_0}{A_0+B_0+C_0},\quad \gamma=\frac{C_0}{A_0+B_0+C_0} \end{gathered} \] Mit anderen Worten, die gemeinsame Rendite unseres Portfolios ist: \[ \begin{gathered} R=\alpha R_A+\beta R_B+\gamma R_C,\quad\text{wobei }\alpha+\beta+\gamma=1. \end{gathered} \tag{5.24}\] Es sind genau diese Kapitalanteile \(\alpha, \beta\) und \(\gamma\), die das Portfolio definieren.

Aber warum sollten Investoren überhaupt Portfolios bilden? Wäre es nicht vernünftiger, das gesamte Kapital in jenes Papier zu investieren, das die höchste Rendite erzielt?

Der wesentliche Grund für die Bildung eines Portfolios ist, dass für die meisten Anlageformen die erzielbaren Renditen keine deterministischen Größen sondern Zufallsgrößen sind. Und es ist die Varianz der Rendite, auf die es ankommt, denn sie ist ein Maß für das Risiko, das mit einer Finanzanlage verbunden ist. Je höher die Varianz der Rendite, umso riskanter ist es, in ein Papier zu investieren.

Wir können uns das intuitiv so veranschaulichen: angenommen, wir haben die Wahl zwischen zwei Wertpapieren \(A\) und \(B\) mit Renditen \(R_A\) und \(R_B\). Weiter angenommen, die erwarteten Renditen seien gleich groß, also \(E(R_A)=E(R_B)\), aber für die Varianzen soll gelten: \[ \begin{gathered} V(R_A)=0,\quad V(R_B)>0. \end{gathered} \] In diesem Fall haben wir gute Gründe dem Wertpapier \(A\) den Vorzug zu geben, denn bei gleichem mittleren Ertrag ist doch der Ertrag, der mit Papier \(B\) erzielt wird, mit einiger Unsicherheit behaftet, die umso größer ist, je größer \(V(R_B)\). Tatsächlich nennt man Anlagen, deren Rendite die Varianz Null hat, risikofrei. Es handelt sich dabei also um Wertpapiere, bei denen die Rendite über einen gewissen Zeitraum garantiert ist.

Wir berechnen nun Erwartungswert und Varianz von \(R\), gegeben in (5.24). Der erwartete Ertrag ist wegen der Linearität des Erwartungswerts (Satz 5.40 (b)): \[ \begin{gathered} E(R)=\alpha E(R_A)+\beta E(R_B)+\gamma E(R_C). \end{gathered} \] Wenn die Renditen \(R_A,R_B\) und \(R_C\) unabhängige Zufallsgrößen sind, dann ist die Varianz und damit ein Maß für das mit dem Portfolio verbundene Risiko wegen Satz 5.54 und Satz 5.56: \[ \begin{gathered} V(R)=\alpha^2V(R_A)+\beta^2V(R_B)+\gamma^2V(R_C). \end{gathered} \tag{5.25}\] Diese Formel, die aus dem Additionsgesetz für Varianzen folgt, hat bemerkenswerte Konsequenzen. Sie erklärt, warum es vernünftig ist, zu diversifizieren.

Das nächste Beispiel zeigt den das Risiko reduzierenden Effekt sehr deutlich.

Musteraufgabe 5.57 (Diversifikation) Eine Investorin bildet ein Portfolio aus drei Wertpapieren \(A, B\) und \(C\). Sie investiert 50% der zur Verfügung stehenden Mittel in Papier \(A\), 30 % in Papier \(B\) und 20 % in Papier \(C\). Die Renditen dieser Wertpapiere sind unabhängige Zufallsgrößen mit den Erwartungswerten 0.08, 0.05 und 0.03 und der gleichen Standardabweichung 0.02. Berechnen Sie Erwartungswert und Standardabweichung der Rendite dieses Portfolios.

Lösung: Die Rendite des Portfolios ist \(R=0.5\cdot R_A+0.3\cdot R_B+0.2\cdot R_C\).

Daraus ergibt sich: \[ \begin{gathered} E(R)=0.5\cdot 0.08+0.3\cdot 0.05+0.2\cdot 0.03= 0.0610\,. \end{gathered} \] und \[ \begin{aligned} V(R)&=0.5^2\cdot V(R_A)+0.3^2\cdot V(R_B)+0.2^2\cdot V(R_C)\\ &=\left[0.5^2+0.3^2+0.2^2\right]\cdot 0.02^2=0.000152\,. \end{aligned} \] Die Standardabweichung der Rendite beträgt daher \(\sqrt{0.000152}=0.012329\). Sie ist damit wesentlich geringer als die Standardabweichung der Rendite jedes der drei Wertpapiere. Das bedeutet, durch Bildung des Portfolios wurde das Anlagerisiko deutlich reduziert. □

Bemerkung 5.58 Zu dieser Aufgabe noch drei Anmerkungen bzw. Fragen:

• Wir haben in dieser Aufgabe und bei der Herleitung von (5.25) ausdrücklich angenommen, dass die Renditen der Wertpapiere unabhängige Zufallsgrößen sind. Was, wenn diese Annahme nicht zutrifft?

• In der Aufgabe waren die das Portfolio definierenden Kapitalanteile vorgegeben. Aber könnten wir diese nicht zu Entscheidungsvariablen machen, und so die Frage stellen: wie sieht ein optimales Portfolio aus?

• Für die Kapitalanteile \(\alpha, \beta\) und \(\gamma\) gilt natürlich \(\alpha+\beta+\gamma=1\), aber das bedeutet nicht, dass alle drei Kapitalanteile positiv sein müssen. Machen negative Kapitalanteile überhaupt Sinn, und was bedeuten sie?

Das sind sehr spannende Fragen, denen wir im Detail in Kapitel 9 auf den Grund gehen werden.

Musteraufgabe 5.59 Ein Investor möchte aus den zwei Wertpapieren \(A\) und \(B\), deren Renditen unabhängige Zufallsgrößen sind, ein Portfolio bilden. Die Standardabweichungen der Renditen sind ihm bekannt: \(\sigma(R_A)=0.7\) und \(\sigma(R_B)=0.8\). Wie muss er die Kapitalanteile der beiden Wertpapiere am Portfolio wählen, sodass das Anlagerisiko minimal wird?

Lösung: Es sei \(\alpha\) der Kapitalanteil von \(A\), dann ist jener von \(B\) \(1-\alpha\). Die gemeinsame Rendite ist daher \(R=\alpha R_A+(1-\alpha) R_B\). Das Maß für das Risiko ist die Varianz von \(R\): \[ \begin{aligned} V(R)&=V(\alpha R_A+(1-\alpha)R_B)=\alpha^2V(R_A)+(1-\alpha)^2V(R_B)\to\min. \end{aligned} \]

Wir bilden die erste Ableitung nach \(\alpha\) und setzen diese Null: \[ \begin{gathered} V'(R)=2\left[\alpha V(R_A)-(1-\alpha)V(R_B)\right]=0,\\[5pt] \alpha=\frac{V(R_B)}{V(R_A)+V(R_B)}=\frac{0.8^2}{0.7^2+0.8^2}=0.5664\,. \end{gathered} \] Optimal wären daher Kapitalanteile von 56.6 % für \(A\) und 43.4 % für \(B\). Dass dies tatsächlich das Minimum der Varianz garantiert, erkennen wir an der 2. Ableitung \(V''(R)=2(V(R_A)+V(R_B))>0\). □

5.3.6 Die Varianz des arithmetischen Mittels

Besonders drastisch ist die Verminderung der Varianz bei der Bildung von Mittelwerten.

Bei einem Zufallsexperiment sei \(X\) eine Zufallsgröße mit dem Erwartungswert \(E(X)=\mu\) und der Varianz \(V(X)=\sigma^2\). Wir führen \(n\) unabhängige Wiederholungen des Zufallsexperiments durch und beobachten dabei \(n\) Kopien \(X_1,\,X_2,\ldots,\,X_n\) der Zufallsgröße \(X\). Den Mittelwert dieser Zufallsgrößen bezeichnen wir mit \[ \begin{gathered} \overline{X}=\frac{X_1+X_2+\cdots+X_n}{n}\,. \end{gathered} \]

Satz 5.60 Es sei \(X\) eine Zufallsgröße mit \(E(X)=\mu\) und \(V(X)=\sigma^2\). Dann gilt \[ \begin{gathered} E(\overline{X})=\mu, \qquad V(\overline{X})=\frac{\sigma^2}{n}. \end{gathered} \]

Begründung: Für den Erwartungswert erhalten wir \[ \begin{aligned} E(\overline{X}) & = E\left(\frac{X_1+X_2+\ldots+X_n}{n}\right) \\ & = \frac{1}{n}(\underbrace{\mu+\ldots+\mu}_{n\text{ Terme}})=\frac{n\mu}{n}=\mu. \end{aligned} \] Für die Varianz gilt \[ \begin{aligned} V(\overline{X}) & = V\left(\frac{X_1+X_2+\ldots+X_n}{n}\right) \\ & = \frac{1}{n^2}(\underbrace{\sigma^2+\ldots+\sigma^2}_{n\text{ Terme}})=\frac{n\sigma^2}{n^2}=\frac{\sigma^2}{n}\,. \end{aligned} \] Beachten Sie, dass hier die Annahme der Unabhängigkeit wesentlich ist! □

Satz 5.60 ist von grundlegender Bedeutung in der Statistik. Hier ist der Erwartungswert \(\mu\) eines Merkmals (Zufallsgröße) \(X\) typischerweise unbekannt, und man möchte auf Grundlage von Stichproben Informationen über \(\mu\) gewinnen. Das arithmetische Mittel ist eine Möglichkeit dafür, und es ist eine überraschend gute. Denn Satz 5.60 hält zwei wichtige Botschaften bereit:

1. Das arithmetische Mittel ist unverzerrt, dies ist die Aussage von \(E(\overline{X})=\mu\). Wir können uns also darauf verlassen, dass \(\overline{X}\) das unbekannte \(\mu\) weder systematisch über- noch unterschätzt.

2. Mit wachsendem Stichprobenumfang \(V(\overline{X})=\sigma^2/n\to 0\), das bedeutet, dass \(\overline{X}\) immer genauer wird, je größer die Stichprobe ist. Bei einer sehr großen Anzahl von Beobachtungen stimmt der Mittelwert daher annähernd mit dem Erwartungswert überein. Dies rechtfertigt nachträglich unsere einführende anschauliche Erklärung des Erwartungswerts.

Den Umstand (b), dass die Varianz eines Mittelwerts mit wachsender Anzahl von Beobachtungen immer kleiner wird, nennt man ebenfalls das Gesetz der großen Zahlen.

Musteraufgabe 5.61 (Qualitätskontrolle) In einem Produktionsvorgang werden Werkstücke mit einer vorgeschriebenen Länge produziert. Die Standardabweichung der Länge beträgt \(3\) mm. Um die Einhaltung des Erwartungswerts der Länge zu kontrollieren, wird die durchschnittliche Länge einer Serie von \(n\) Werkstücken kontrolliert. Wie groß muss die Serie sein, damit die Standardabweichung der Durchschnittslänge \(0.5\) mm beträgt?

Lösung: Die durchschnittliche Länge einer Serie ist durch den Mittelwert gegeben und die Varianz des Mittelwertes ist \(V(\overline{X}) = \sigma ^2/ n\). Daher beträgt die Standardabweichung der Durchschnittslänge einer Serie von \(n\) Werkstücken \(3/\sqrt{n}\). Um zu erreichen, dass \[ \begin{gathered} \frac{3}{\sqrt{n}}=0.5 \end{gathered} \] ist, muss \(\sqrt{n}=6\), also \(n=36\) betragen. □

5.4 Die Normalverteilung

Die Normalverteilung ist eine der wichtigsten, wenn nicht die wichtigste Wahrscheinlichkeitverteilung. Der Begriff Normalverteilung geht vermutlich auf Lambert Adolphe Jacques Quetelet (1796-1876) zurück, einen belgischen Statistiker, der (wie andere schon vor ihm) bei seinen Untersuchungen bemerkt hatte, dass viele Häufigkeitsverteilungen von biologischen Merkmalen, wie z.B. die Körpergröße von Menschen, einen typischen glockenförmigen Verlauf zeigen.

Die Normalverteilung ist eine stetige Verteilung, die durch lediglich zwei Parameter bestimmt ist, nämlich durch ihren Erwartungswert \(\mu\) und ihre Varianz \(\sigma^2\).

Definition 5.62 Eine Zufallsgröße \(X\) heißt normalverteilt, wenn ihre Dichtefunktion gegeben ist durch: \[ \begin{gathered} f(x)=%\frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{(x-\mu)^2}{2\sigma^2}} = \frac{1}{\sigma\sqrt{2\pi}}\exp\left[-\frac{(x-\mu)^2}{2\sigma^2}\right]. \end{gathered} \tag{5.26}\] Es gilt: \(E(X)=\mu\) und \(V(X)=\sigma^2\).

Die Dichte \(f(x)\) zeigt eine schöne glöckenförmige Form, symmetrisch um den Erwartungswert \(\mu\). Je größer die Standardabweichung \(\sigma\) ist, umso flacher verläuft die Dichte, je kleiner \(\sigma\), umso stärker ist \(f(x)\) um \(\mu\) zentriert.

Abbildung 5.10: Dichte der Normalverteilung.

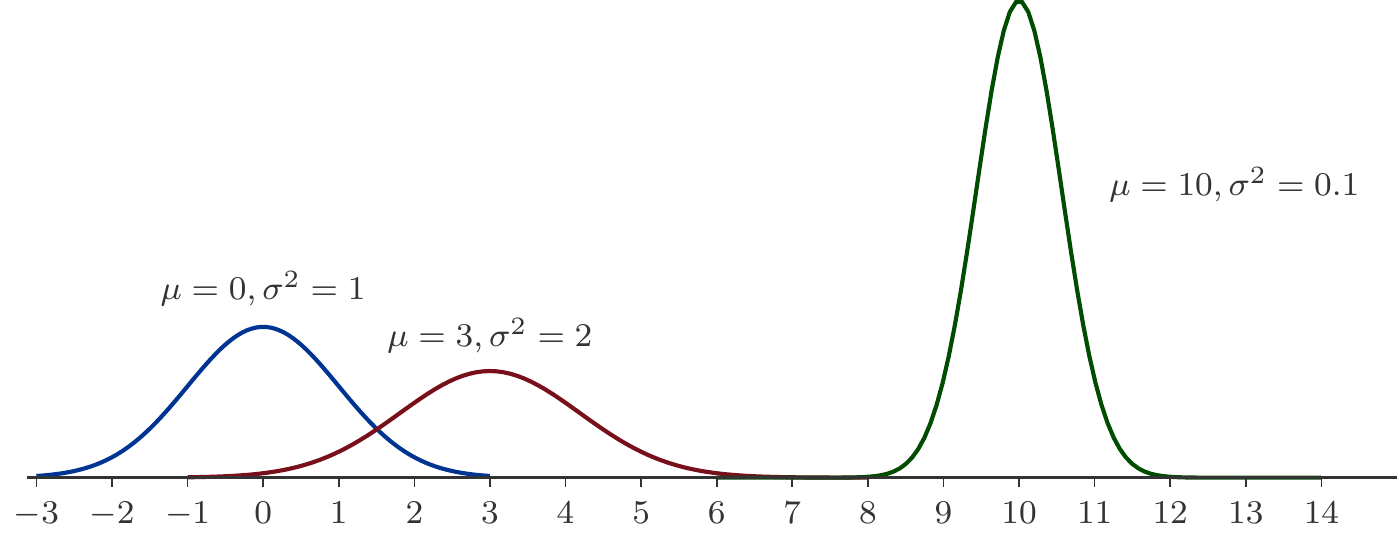
Wahrscheinlichkeiten werden, wie schon oben erläutert, durch Flächeninhalte unterhalb der Dichte definiert: \[ \begin{gathered} P(a<X\le b)=\int_a^bf(x)\,\mathrm{d}x. \end{gathered} \] Leider ist es nicht möglich, die Verteilungsfunktion \(F(x)=P(X\le x)\) mit Hilfe endlich vieler Terme in geschlossener Form anzugeben. Daher müssen Wahrscheinlichkeiten auf numerischem Weg ermittelt werden. Dabei nutzt man die Tatsache aus, dass lineare Funktionen normalverteilter Zufallsgrößen selber wieder normalverteilt sind. Insbesondere ist die Zufallsgröße \(Z\), definiert durch \[ \begin{gathered} Z=\frac{X-\mu}{\sigma}, \end{gathered} \tag{5.27}\] normalverteilt mit Erwartungswert \(\mu=0\) und Standardabweichung \(\sigma=1\). Die Transformation (5.27) nennt man Standardisieren, die Verteilung von \(Z\) heißt Standardnormalverteilung.

5.4.1 Die Standardnormalverteilung

Die Dichte einer standardnormalverteilten Zufallsgröße \(Z\) wird mit \(\phi(z)\) bezeichnet: \[ \begin{gathered} \phi(z)=\frac{1}{\sqrt{2\pi}}e^{-z^2/2}. \end{gathered} \] Der Graph von \(\phi(z)\) ist in Abbildung 5.10 (links) zu sehen. Die Verteilungsfunktion ist: \[ \begin{gathered} P(Z\le a)=\Phi(a)=\int_{-\infty}^a\phi(z)\,\mathrm{d}z,\qquad a\in\mathbb R. \end{gathered} \] Die Funktionswerte \(\Phi(z)\) können mit Computerprogrammen berechnet oder in Tabellen nachgeschlagen werden, siehe Abschnitt 5.4.4. Ihre Verwendung ist denkbar einfach, es gelten die folgenden Regeln: \[ \begin{aligned} P(Z\le a) & = \Phi(a), \end{aligned} \tag{5.28}\] \[ \begin{aligned} P(a<Z\le b) & = \Phi(b)-\Phi(a). \end{aligned} \tag{5.29}\] Wegen der Symmetrie der Dichte der Standardnormalverteilung um Null gilt außerdem: \[ \begin{gathered} \Phi(0)=0.5,\qquad \Phi(-a)=1-\Phi(a)\quad\text{für alle }a\in\mathbb R. \end{gathered} \tag{5.30}\] Die folgende Musteraufgabe demonstriert, wie diese Tabelle verwendet wird.

Musteraufgabe 5.63 Eine Zufallsgröße \(Z\) sei standardnormalverteilt. Zu berechnen sind mit Hilfe von Abschnitt 5.4.4: \[ \begin{gathered} \begin{array}{clccl} (a) & P(Z\le 1) & \quad & (b) & P(Z>-0.8) \\[3pt] (c) & P(-0.5<Z\le2) & \quad & (d) & P(|Z|\le 1.2) \\[3pt] (e) & P(|Z|>2) & \quad & (f) & P(Z^2<2) \\[3pt] (g) & P(3Z-1> 2) & \quad & (h) & P(4-Z\le Z) \\[3pt] (i) & P(|2Z+1|<1) \end{array} \end{gathered} \]

Lösung:

(a) Hier suchen wir direkt den Wert der Verteilungsfunktion:

(b) Wir gehen zuerst auf das Gegenereignis:

(c) Das ist eine direkte Anwendung von Regel (5.29):

(d) Um diese Wahrscheinlichkeit berechnen zu können, ist es erst erforderlich, die Ungleichung \(|Z|\le 1.2\) zu lösen. Das ist einfach: alle reellen Zahlen im Intervall \([-1.2,1.2]\) haben die Eigenschaft \(|Z|\le 1.2\). D.h. die Ereignisse \(\{|Z|\le 1.2\}\) und \(\{-1.2\le Z\le 1.2\}\) sind äquivalent und haben daher die gleiche Wahrscheinlichkeit:

(e) ist völlig analog zu (d): wir gehen nur vorher auf das Gegenereignis: \[ \begin{aligned} P(|Z|>2)&=1-P(|Z|\le 2) = 1 - P(-2\le Z\le 2)\\[4pt] &=1-\left[\Phi(2)-\Phi(-2)\right]\\[4pt] &= 1-[0.977-0.023]=0.046 \end{aligned} \] (f) Um Tabelle 1 verwenden zu können, müssen wir zuerst die quadratische Ungleichung \(Z^2<2\) lösen. Alle reellen Zahlen im Intervall \((-\sqrt{2},\;+\sqrt{2})\) erfüllen diese Ungleichung. Daher: \[ \begin{aligned} P(Z^2<2)&= P(-\sqrt{2}<Z<\sqrt{2})\simeq \Phi(1.41)-\Phi(-1.41)\\ &=0.921-0.079=0.842,\end{aligned} \] dabei haben wir \(\sqrt{2}\) auf zwei Stellen gerundet, denn Tabelle 1 erlaubt keine höhere Genauigkeit.

(g) Wir lösen die Ungleichung \[ \begin{gathered} 3Z-1>2\implies 3Z>3\implies Z>1. \end{gathered} \] Daher: \[ \begin{aligned} P(3Z-1>2)&=P(Z>1)=1-P(Z\le 1) \\ &=1-\Phi(1)=1-0.841=0.159 \end{aligned} \]

(h) Aus \(4-Z\le Z\) folgt \(4\le 2Z\implies Z\ge 2\). Somit: \[ \begin{aligned} P(4-Z\le Z)&=P(Z\ge 2)=1-P(Z<2)\\ &=1-\Phi(2)=1-0.977=0.023 \end{aligned} \] (i) Vergleiche (d): \[ \begin{aligned} P(|2Z+1|<1)&=P(-1<2Z+1<1)=P(-2<2Z<0)\\ &=P(-1<Z<0)=\Phi(0)-\Phi(-1)\\ &=0.5-0.159=0.341 \end{aligned} \]

Quantile

Viele Anwendungsprobleme erfordern die Berechnung sogenannter Quantile der Standardnormalverteilung. Dabei geht es um die Lösung von Gleichungen der Form \[ \begin{gathered} P(Z\le z)=\Phi(z)=\alpha, \end{gathered} \] wobei \(\alpha\in(0,1)\) gegeben ist und \(z\) gesucht wird. Die Lösung dieser Aufgabe ist das \(\alpha\)-Quantil. Das \(\alpha\)-Quantil ist also jener Wert \(z\), den die Zufallsgröße mit Wahrscheinlichkeit \(\alpha\) nicht überschreitet. Mit anderen Worten, das Quantil ist die Umkehrfunktion \(\Phi^{-1}\) der Verteilungsfunktion \(\Phi\).

Definition 5.64 Das \(\alpha\)-Quantil \(\Phi^{-1}(\alpha)\) der Standardnormalverteilung erfüllt die Gleichung \[ \begin{gathered} P(Z\le \Phi^{-1}(\alpha))=\alpha,\qquad \alpha\in(0,1). \end{gathered} \] Das bedeutet: \[ \begin{gathered} \Phi(z)=\alpha\Leftrightarrow z=\Phi^{-1}(\alpha). \end{gathered} \]

Das \(\alpha\)-Quantil teilt die Fläche unterhalb der Dichte der Standardnormalverteilung in zwei Teile, von denen der linke Teil den Flächeninhalt \(\alpha\) besitzt und der rechte Teil den Flächeninhalt \(1-\alpha\). Die Abbildung 5.11 veranschaulicht den Begriff des Quantils.

Abbildung 5.11: Das \(\alpha\)-Quantil.

Da die Dichte der Standardnormalverteilung symmetrisch um Null ist, gilt: \[ \begin{gathered} \Phi^{-1}(0.5)=0,\quad \Phi^{-1}(\alpha)=-\Phi^{-1}(1-\alpha). \end{gathered} \]

Auch im Fall von Quantilen der Standardnormalverteilung benutzt man entweder Computerprogramme oder Tabellen, siehe Abschnitt 5.4.4.

Musteraufgabe 5.65 Die Zufallsgröße \(Z\) ist standardnormalverteilt.

1. Man finde jenen Wert, den \(Z\) mit der Wahrscheinlichkeit 0.9 nicht überschreitet.

2. Man finde jenen Wert, den \(Z\) mit der Wahrscheinlichkeit 0.6 überschreitet.

3. Finde ein \(a\), sodass \(P(-a<Z\le a)=0.84\).

Lösung:

(a) \(P(Z\le z)=\Phi(z)=0.9 \implies z=\Phi^{-1}(0.9)=1.2816.\)

(b) \(P(Z>z)=0.6 \implies P(Z\le z)=\Phi(z)=0.4 \implies z=\Phi^{-1}(0.4)=-0.2533.\)

(c) Wir benützen die Symmetrieregel (5.30), \(\Phi(-a)=1-\Phi(a)\): \[ \begin{aligned} P(-a<Z\le a)&=0.84\\ \Phi(a)-\Phi(-a)&=0.84\\ \Phi(a)-\left[1-\Phi(a)\right]&=0.84\qquad\text{(Symmetrieregel)}\\ 2\Phi(a)&=1.84\\ \Phi(a)&=0.92\qquad\implies a=\Phi^{-1}(0.92)=1.4051\,. \end{aligned} \]

5.4.2 Anwendungen der Normalverteilung

Man steht oft vor dem Problem, dass man Wahrscheinlichkeiten in Zusammenhang mit einer Zufallsgröße berechnen soll, ohne dass man die Verteilung der Zufallsgröße genau kennt. In solchen Fällen ist es hilfreich, wenn man weiß, dass die Zufallsgröße \(X\) annähernd normalverteilt ist mit bekanntem Erwartungswert \(\mu\) und Varianz \(\sigma^2\). In solchen Fällen werden Wahrscheinlichkeiten und Quantile durch Standardisieren \[ \begin{gathered} Z=\frac{X-\mu}{\sigma} \end{gathered} \] mit Hilfe der Standardnormalverteilung berechnet.

Musteraufgabe 5.66 (Intelligenztests) Der Intelligenzquotient (IQ) ist in einer Population in exzellenter Näherung normalverteilt mit \(\mu=100\) und \(\sigma=15\).

1. Jemand gilt als hochbegabt, wenn der \(\mathit{IQ}>130\). Wie groß ist der Anteil der Hochbegabten in der Population?

2. Welchen IQ müsste jemand im Test erreichen, um zu den Top-25 % zu gehören?

3. In welchem symmetrischen Intervall um den Erwartungswert liegen \(2/3\) der Population?

Lösung:

(a) \(P(\mathit{IQ}>130)=1-P(\mathit{IQ}\le 130)\), es genügt also die Wahrscheinlichkeit \(P(\mathit{IQ}\le 130)\) zu berechnen. Dazu standardisieren wir: \[ \begin{aligned} P(\mathit{IQ}\le 130)&=P\left(\underbrace{\frac{\mathit{IQ}-100}{15}}_{Z}\le \frac{130-100}{15}\right)=P\left(Z\le 2\right). \end{aligned} \] Die Zufallsgröße \(Z=\dfrac{\mathit{IQ}-100}{15}\) ist aber standardnormalverteilt. Das bedeutet: \[ \begin{aligned} P\left(Z\le 2\right)&=\Phi(2)=0.977, \end{aligned} \] und daher ist der Anteil der Hochbegabten \(1-0.977=0.023\), d.h. 2.3 %.

(b) Wir suchen ein kritisches Testergebnis \(a\), sodass \(P(\mathit{IQ}>a)=0.25\), oder über das Gegenereignis: \(P(\mathit{IQ}\le a)=0.75\). Wir standardisieren wieder: \[ \begin{aligned} P(\mathit{IQ}\le a)&=P\left(\frac{\mathit{IQ}-100}{15}\le \frac{a-100}{15}\right) =0.75, \end{aligned} \] oder: \[ \begin{aligned} P\left(Z\le \frac{a-100}{15}\right)&=\Phi\left(\frac{a-100}{15}\right)=0.75\,. \end{aligned} \] Die letzte Gleichung lösen wir mittels der Umkehrfunktion \(\Phi^{-1}\): \[ \begin{gathered} \frac{a-100}{15}=\Phi^{-1}(0.75)=0.6745\\ \implies a=100+15\cdot 0.6745=110.1175\,. \end{gathered} \] Jemand müsste also einen Score von wenigstens 110 erreichen um zu den besten 25 % der Population zu gehören.

(c) Das gesuchte Intervall ist von der Form \([100-a, 100+a]\). Die Wahrscheinlichkeit in dieses Intervall zu fallen, muss \(2/3\) betragen: \[ \begin{gathered} P(100-a\le \mathit{IQ}\le 100+a)=\frac{2}{3},\\[4pt] P\left(\frac{100-a-100}{15}\le \frac{\mathit{IQ}-100}{15} \le \frac{100+a-100}{15}\right)=\frac{2}{3},\\[4pt] P\left(-\frac{a}{15}\le Z\le \frac{a}{15}\right)=\frac{2}{3}\,. \end{gathered} \] Das vereinfachen wir nun mit der Symmetrieregel (5.30): \[ \begin{gathered} \Phi\left(\frac{a}{15}\right)-\Phi\left(-\frac{a}{15}\right)=\frac{2}{3},\\[4pt] \Phi\left(\frac{a}{15}\right)-\left[1-\Phi\left(\frac{a}{15}\right)\right]=\frac{2}{3},\\[4pt] \Phi\left(\frac{a}{15}\right)=\frac{5}{6}=0.8333\implies \frac{a}{15}=\Phi^{-1}(0.83)=0.9542,\\[4pt] a=15\cdot 0.9542=14.3130\simeq 14. \end{gathered} \] Das heißt: in dem Intervall \([100\pm 14]=[86,114]\) liegen ca. 2/3 der Population. □

Musteraufgabe 5.67 (Finanzmathematik) Die Rendite eines Wertpapiers sei normalverteilt mit Mittelwert 0.08 und Standardabweichung 0.05.

1. Wie groß ist die Wahrscheinlichkeit, dass die Rendite negativ ist?

2. Welchen Wert unterschreitet die Rendite mit einer Wahrscheinlichkeit von 1 Prozent?

Lösung: Es sei \(X\) die Rendite des Wertpapiers.
(a) Wir interessieren uns für \(P(X<0)\): \[ \begin{aligned} P(X<0) & = P\left(Z<\frac{0-0.08}{0.05}\right)\\ & = P(Z<-1.6) = \Phi(-1.6)=0.055. \end{aligned} \] (b) Wir suchen \(x\), sodass \(P(X<x)=0.01\). \[ \begin{gathered} P(X<x)=P\left(Z\le \frac{x-0.08}{0.05}\right)=0.01\\[4pt] \frac{x-0.08}{0.05}=\Phi^{-1}(0.01)=-2.3263\\ \implies x=0.08-0.05\cdot 2.3263 =-0.0363\,. \end{gathered} \]

□

Musteraufgabe 5.68 Der tägliche Stromverbrauch eines Betriebes (in MWh) ist etwa normalverteilt mit Mittelwert 6.5 und Varianz 4.6. Eine eigene Stromversorgung für diesen Betrieb liefert täglich 8 MWh. Wie groß ist die Wahrscheinlichkeit, dass sich der Betrieb an einem bestimmten Tag selbst versorgen kann?

Lösung: Es sei \(X\) der tägliche Stromverbrauch. Dann ist \[ \begin{gathered} P(X\le 8)=P\left(Z\le\frac{8-6.5}{\sqrt{4.6}}\right)= P(Z\le 0.7)=0.758\,. \end{gathered} \] Die Wahrscheinlichkeit, dass an einem bestimmten Tag höchstens 8 MWh verbraucht werden, liegt bei ca. \(76\%\). □

Musteraufgabe 5.69 Die jährliche Nachfrage nach einem Produkt ist eine normalverteilte Zufallsgröße mit Erwartungswert 280 und Varianz 1600. Wieviel Mengeneinheiten müssten produziert werden, damit die Wahrscheinlichkeit dafür, dass die Nachfrage die produzierte Menge überschreitet, nur 1 Prozent beträgt?

Lösung: Es sei \(X\) die jährliche Nachfrage und \(x\) sei die produzierte Menge. Wir interessieren uns für jenen Wert von \(x\), sodass \(P(X>x)=0.01\). Da \[ \begin{gathered} P(X>x)=P\left(Z>\frac{x-280}{\sqrt{1600}}\right)=0.01 \end{gathered} \] sein soll, folgt: \[ \begin{gathered} P\left(Z\le\frac{x-280}{40}\right)=0.99\implies \frac{x-280}{40}=\Phi^{-1}(0.99)=2.3263. \end{gathered} \] Daher beträgt die erforderliche Produktionsmenge: \[ \begin{gathered} x=280+40\cdot 2.3263=373.05\text{ Mengeneinheiten}. \end{gathered} \] □

5.4.3 Der zentrale Grenzwertsatz

Die Unterstellung einer Normalverteilung ist insbesondere immer dann gerechtfertigt, wenn es um die Wahrscheinlichkeitsverteilung von Summen und Mittelwerten geht. Der Grund dafür ist der zentrale Grenzwertsatz, neben dem Gesetz der großen Zahlen eine weitere fundamentale Gesetzmäßigkeit der Wahrscheinlichkeitsrechnung.

Satz 5.70 (Zentraler Grenzwertsatz) Es sei \(X\) eine Zufallsgröße mit \(E(X)=\mu\) und \(V(X)=\sigma^2\). Dann sind die Summe \(S_n\) und der Mittelwert \(\overline{X}\) von \(n\) unabhängigen Kopien der Zufallsgröße annähernd normalverteilt, wobei: \[ \begin{aligned} E(S_n)&=n\mu & V(S_n)&=n\sigma^2, \\ \end{aligned} \tag{5.31}\]

\[ \begin{aligned} E(\overline{X})&=\mu & V(\overline{X})&=\frac{\sigma^2}{n}\,. \end{aligned} \tag{5.32}\]

Für einen mathematischen Beweis dieses fundamentalen Sachverhalts der Wahrscheinlichkeitstheorie fehlen uns hier die Mittel. Es ist aber sehr einfach, den zentralen Grenzwertsatz anzuwenden.

Musteraufgabe 5.71 (Qualitätskontrolle) In einem Produktionsvorgang werden Werkstücke mit einer vorgeschriebenen Länge von \(1\) \(m\) produziert. Die Standardabweichung der Länge beträgt \(3\) mm. Um die Einhaltung des Erwartungswerts der Länge zu kontrollieren, wird die durchschnittliche Länge einer Serie von \(50\) Werkstücken kontrolliert. Wie groß ist die Wahrscheinlichkeit dafür, dass dieser Messwert im Bereich \(1000\pm 1\) mm liegt, sofern der Erwartungswert der Länge eines Werkstücks tatsächlich \(1\) \(m\) beträgt?

Lösung: Wir rechnen in der Einheit 1 mm. Wegen (5.31) gilt: \[ \begin{gathered} n=50,\qquad E(\overline{X})=1000,\qquad V(\overline{X})=\frac{3^2}{50}=0.18\,. \end{gathered} \] Die Wahrscheinlichkeit, dass \(\overline{X}\) in das vorgegebene Toleranzintervall \(1000\pm 1\) fällt, ist: \[ \begin{aligned} P(999<\overline{X}< 1001) &=P\left(\frac{999-1000}{\sqrt{0.18}}<Z< \frac{1001-1000}{\sqrt{0.18}}\right)\\[4pt] &=P(-2.36<Z< 2.36) \\[4pt] &=\Phi(2.36)-\Phi(-2.36)\\[4pt] &=0.991-0.009=0.982\,. \end{aligned} \] □

5.4.4 Berechnung der Standardnormalverteilung

Wie im Laufe dieses Abschnitts bereits mehrmals erwähnt werden für die Berechnung von Wahrscheinlichkeiten bzw. Quantilen der (Standard-) Normalverteilung in der Praxis in aller Regel Computerprogramme verwendet. Diese Programme stellen dann folgende zwei Funktionen zur Verfügung:

• Verteilungsfunktion: \(\Phi(x) = \mathsf{P}(Z \le x) = \alpha\).
• Quantilsfunktion (oder inverse Verteilungsfunktion): \(\Phi^{-1}(\alpha) = x\).

Während nämlich die Dichtefunktion \(\phi(x)\) der Standardnormalverteilung einfach mit Hilfe der Exponentialfunktion mit einem Taschenrechner berechent werden kann, ist dies bei der Verteilungsfunktion und ihrer Inversen nicht der Fall. Im Folgenden werden deshalb einige Möglichkeiten aufgelistet diese beiden Funktionen zu berechnen. Zusätzlich zu verschiedenen Computerprogrammen werden dabei auch noch Tabellen bereitgestellt, in denen man die Wahrscheinlichkeiten bzw. Quantile nachschlagen kann.

Tabellen

• Verteilungsfunktion: In der ersten folgenden Tabelle sind die Werte von \(\Phi(x)\) eingetragen für \(x\) mit zwei Nachkommastellen von \(-2.99, \dots, 2.99\).
• Quantilsfunktion: In der zweiten folgenden Tabelle sind die Werte von \(\Phi^{-1}(\alpha)\) eingetragen für \(\alpha\) mit zwei Nachkommastellen von \(0.01, \dots, 0.99\) sowie \(0.975\) und \(0.995\).

R

• Verteilungsfunktion: pnorm(x)
• Quantilsfunktion: qnorm(alpha)

Zusätzlich kann in beiden Funktionen auch ein anderer Mittelwert als die Voreinstellung mean = 0 sowie eine andere Standardabweichung als sd = 1 angegeben werden. Weitere Details sind auf ?pnorm dokumentiert.

GeoGebra (CAS-Modus)

• Verteilungsfunktion: Normal(0, 1, x)
• Quantilsfunktion: InversNormal(0, 1, alpha)

Der Erwartungswert (mew) und die Standardabweichung (sigma) müssen also immer mit angegeben werden. Der Code oben verwendet daher 0 und 1 um die Standardnormalverteilung zu erhalten.

Excel & LibreOffice

• Verteilungsfunktion: NORM.S.VERT(x, 1) (deutsch) bzw.
  NORM.S.DIST(x, 1) (englisch)
• Quantilsfunktion: NORM.S.INV(alpha)

Die 1 am Ende des Aufrufs der VERT/DIST Funktionen gibt an, dass die Verteilungsfunktion berechnet werden soll. Setzt man den Wert auf 0 wird die Dichtefunktion berechnet.

Zusätzlich zu den Funktionen mit .S. im Namen (für die Standardnormalverteilung) gibt es auch analoge Funktionen für Normalverteilungen, bei denen man Mittelwert und Standardabweichung angeben muss.

• Verteilungsfunktion: NORM.VERT(x, 0, 1, 1) (deutsch) bzw.
  NORM.DIST(x, 0, 1, 1) (englisch)
• Quantilsfunktion: NORM.INV(alpha, 0, 1)

WolframAlpha

• Verteilungsfunktion: CDF[NormalDistribution[0, 1], x]
• Quantilsfunktion: InverseCDF[NormalDistribution[0, 1], alpha]

Der Erwartungswert und die Standardabweichung müssen also immer mit angegeben werden. Der Code oben verwendet daher 0 und 1 um die Standardnormalverteilung zu erhalten.

Verteilungsfunktion der Standardnormalverteilung

	0.00	0.01	0.02	0.03	0.04	0.05	0.06	0.07	0.08	0.09
-2.9	0.002	0.002	0.002	0.002	0.002	0.002	0.002	0.001	0.001	0.001
-2.8	0.003	0.002	0.002	0.002	0.002	0.002	0.002	0.002	0.002	0.002
-2.7	0.003	0.003	0.003	0.003	0.003	0.003	0.003	0.003	0.003	0.003
-2.6	0.005	0.005	0.004	0.004	0.004	0.004	0.004	0.004	0.004	0.004
-2.5	0.006	0.006	0.006	0.006	0.006	0.005	0.005	0.005	0.005	0.005
-2.4	0.008	0.008	0.008	0.008	0.007	0.007	0.007	0.007	0.007	0.006
-2.3	0.011	0.010	0.010	0.010	0.010	0.009	0.009	0.009	0.009	0.008
-2.2	0.014	0.014	0.013	0.013	0.013	0.012	0.012	0.012	0.011	0.011
-2.1	0.018	0.017	0.017	0.017	0.016	0.016	0.015	0.015	0.015	0.014
-2.0	0.023	0.022	0.022	0.021	0.021	0.020	0.020	0.019	0.019	0.018
-1.9	0.029	0.028	0.027	0.027	0.026	0.026	0.025	0.024	0.024	0.023
-1.8	0.036	0.035	0.034	0.034	0.033	0.032	0.031	0.031	0.030	0.029
-1.7	0.045	0.044	0.043	0.042	0.041	0.040	0.039	0.038	0.038	0.037
-1.6	0.055	0.054	0.053	0.052	0.051	0.049	0.048	0.047	0.046	0.046
-1.5	0.067	0.066	0.064	0.063	0.062	0.061	0.059	0.058	0.057	0.056
-1.4	0.081	0.079	0.078	0.076	0.075	0.074	0.072	0.071	0.069	0.068
-1.3	0.097	0.095	0.093	0.092	0.090	0.089	0.087	0.085	0.084	0.082
-1.2	0.115	0.113	0.111	0.109	0.107	0.106	0.104	0.102	0.100	0.099
-1.1	0.136	0.133	0.131	0.129	0.127	0.125	0.123	0.121	0.119	0.117
-1.0	0.159	0.156	0.154	0.152	0.149	0.147	0.145	0.142	0.140	0.138
-0.9	0.184	0.181	0.179	0.176	0.174	0.171	0.169	0.166	0.164	0.161
-0.8	0.212	0.209	0.206	0.203	0.200	0.198	0.195	0.192	0.189	0.187
-0.7	0.242	0.239	0.236	0.233	0.230	0.227	0.224	0.221	0.218	0.215
-0.6	0.274	0.271	0.268	0.264	0.261	0.258	0.255	0.251	0.248	0.245
-0.5	0.309	0.305	0.302	0.298	0.295	0.291	0.288	0.284	0.281	0.278
-0.4	0.345	0.341	0.337	0.334	0.330	0.326	0.323	0.319	0.316	0.312
-0.3	0.382	0.378	0.374	0.371	0.367	0.363	0.359	0.356	0.352	0.348
-0.2	0.421	0.417	0.413	0.409	0.405	0.401	0.397	0.394	0.390	0.386
-0.1	0.460	0.456	0.452	0.448	0.444	0.440	0.436	0.433	0.429	0.425
0.0	0.500	0.500	0.500	0.500	0.500	0.500	0.500	0.500	0.500	0.500
0.1	0.540	0.544	0.548	0.552	0.556	0.560	0.564	0.567	0.571	0.575
0.2	0.579	0.583	0.587	0.591	0.595	0.599	0.603	0.606	0.610	0.614
0.3	0.618	0.622	0.626	0.629	0.633	0.637	0.641	0.644	0.648	0.652
0.4	0.655	0.659	0.663	0.666	0.670	0.674	0.677	0.681	0.684	0.688
0.5	0.691	0.695	0.698	0.702	0.705	0.709	0.712	0.716	0.719	0.722
0.6	0.726	0.729	0.732	0.736	0.739	0.742	0.745	0.749	0.752	0.755
0.7	0.758	0.761	0.764	0.767	0.770	0.773	0.776	0.779	0.782	0.785
0.8	0.788	0.791	0.794	0.797	0.800	0.802	0.805	0.808	0.811	0.813
0.9	0.816	0.819	0.821	0.824	0.826	0.829	0.831	0.834	0.836	0.839
1.0	0.841	0.844	0.846	0.848	0.851	0.853	0.855	0.858	0.860	0.862
1.1	0.864	0.867	0.869	0.871	0.873	0.875	0.877	0.879	0.881	0.883
1.2	0.885	0.887	0.889	0.891	0.893	0.894	0.896	0.898	0.900	0.901
1.3	0.903	0.905	0.907	0.908	0.910	0.911	0.913	0.915	0.916	0.918
1.4	0.919	0.921	0.922	0.924	0.925	0.926	0.928	0.929	0.931	0.932
1.5	0.933	0.934	0.936	0.937	0.938	0.939	0.941	0.942	0.943	0.944
1.6	0.945	0.946	0.947	0.948	0.949	0.951	0.952	0.953	0.954	0.954
1.7	0.955	0.956	0.957	0.958	0.959	0.960	0.961	0.962	0.962	0.963
1.8	0.964	0.965	0.966	0.966	0.967	0.968	0.969	0.969	0.970	0.971
1.9	0.971	0.972	0.973	0.973	0.974	0.974	0.975	0.976	0.976	0.977
2.0	0.977	0.978	0.978	0.979	0.979	0.980	0.980	0.981	0.981	0.982
2.1	0.982	0.983	0.983	0.983	0.984	0.984	0.985	0.985	0.985	0.986
2.2	0.986	0.986	0.987	0.987	0.987	0.988	0.988	0.988	0.989	0.989
2.3	0.989	0.990	0.990	0.990	0.990	0.991	0.991	0.991	0.991	0.992
2.4	0.992	0.992	0.992	0.992	0.993	0.993	0.993	0.993	0.993	0.994
2.5	0.994	0.994	0.994	0.994	0.994	0.995	0.995	0.995	0.995	0.995
2.6	0.995	0.995	0.996	0.996	0.996	0.996	0.996	0.996	0.996	0.996
2.7	0.997	0.997	0.997	0.997	0.997	0.997	0.997	0.997	0.997	0.997
2.8	0.997	0.998	0.998	0.998	0.998	0.998	0.998	0.998	0.998	0.998
2.9	0.998	0.998	0.998	0.998	0.998	0.998	0.998	0.999	0.999	0.999

Quantile der Standardnormalverteilung

\(\alpha\)	\(\Phi^{-1}(\alpha)\)	\(\alpha\)	\(\Phi^{-1}(\alpha)\)	\(\alpha\)	\(\Phi^{-1}(\alpha)\)
0.01	-2.3263	0.34	-0.4125	0.67	0.4399
0.02	-2.0537	0.35	-0.3853	0.68	0.4677
0.03	-1.8808	0.36	-0.3585	0.69	0.4959
0.04	-1.7507	0.37	-0.3319	0.70	0.5244
0.05	-1.6449	0.38	-0.3055	0.71	0.5534
0.06	-1.5548	0.39	-0.2793	0.72	0.5828
0.07	-1.4758	0.40	-0.2533	0.73	0.6128
0.08	-1.4051	0.41	-0.2275	0.74	0.6433
0.09	-1.3408	0.42	-0.2019	0.75	0.6745
0.10	-1.2816	0.43	-0.1764	0.76	0.7063
0.11	-1.2265	0.44	-0.1510	0.77	0.7388
0.12	-1.1750	0.45	-0.1257	0.78	0.7722
0.13	-1.1264	0.46	-0.1004	0.79	0.8064
0.14	-1.0803	0.47	-0.0753	0.80	0.8416
0.15	-1.0364	0.48	-0.0502	0.81	0.8779
0.16	-0.9945	0.49	-0.0251	0.82	0.9154
0.17	-0.9542	0.50	0.0000	0.83	0.9542
0.18	-0.9154	0.51	0.0251	0.84	0.9945
0.19	-0.8779	0.52	0.0502	0.85	1.0364
0.20	-0.8416	0.53	0.0753	0.86	1.0803
0.21	-0.8064	0.54	0.1004	0.87	1.1264
0.22	-0.7722	0.55	0.1257	0.88	1.1750
0.23	-0.7388	0.56	0.1510	0.89	1.2265
0.24	-0.7063	0.57	0.1764	0.90	1.2816
0.25	-0.6745	0.58	0.2019	0.91	1.3408
0.26	-0.6433	0.59	0.2275	0.92	1.4051
0.27	-0.6128	0.60	0.2533	0.93	1.4758
0.28	-0.5828	0.61	0.2793	0.94	1.5548
0.29	-0.5534	0.62	0.3055	0.95	1.6449
0.30	-0.5244	0.63	0.3319	0.96	1.7507
0.31	-0.4959	0.64	0.3585	0.97	1.8808
0.32	-0.4677	0.65	0.3853	0.975	1.9600
0.33	-0.4399	0.66	0.4125	0.98	2.0537
				0.99	2.3263
				0.995	2.5758

5.5 Die Binomialverteilung

5.5.1 Bernoulli-Experimente

An den Beginn dieses Kapitels stellten wir den zentralen Begriff des Zufallsexperiments. So nannten wir jedes Experiment, das wenigstens zwei mögliche Ergebnisse hat. Diesen Abschnitt des Kapitels widmen wir einer speziellen Familie von Experimenten, die genau zwei Ergebnisse haben, sogenannte Bernoulli-Experimente¹. Diese sind durch folgende Eigenschaften charakterisiert:

• Das Zufallsexperiment besteht aus Versuchen mit jeweils zwei alternativen Ergebnissen, Erfolg \(S\) (success) und Misserfolg \(F\) (failure).

• Die Wahrscheinlichkeit eines Erfolgs \(P(S)=p\) nennen wir Erfolgswahrscheinlichkeit, und \(P(F)=1-p\).

• Das Experiment wird \(n\)–mal wiederholt.

• Die Wiederholungen sind unabhängig voneinander und erfolgen unter gleichen Versuchsbedingungen, sodass \(p\) in allen Experimenten gleich ist.

Wir interessieren uns für die Anzahl der Erfolge \(S_n\) in \(n\) Experimenten. Offenbar kann die Zufallsgröße \(S_n\) nur die Werte \(0,1,\ldots,n\) annehmen.

Was ist ihre Wahrscheinlichkeitsverteilung?

Beispiel 5.72 (Stochastische Prozesskontrolle)

Im Rahmen der Qualitätskontrolle werden aus der laufenden Produktion Stichproben der Größe \(n\) gezogen. Die Werkstücke in der Stichprobe werden darauf überprüft, ob sie den Qualitätsanforderungen genügen. \(S\) sei das Ereignis, dass ein überprüftes Stück den Anforderungen nicht entspricht. Die Wahrscheinlichkeit \(p=P(S)\) heißt Ausschussrate des Prozesses. \(S_n\) ist die Anzahl der nicht entsprechenden Items in einer Stichprobe. Wenn \(S_n\) zu groß ist, dann besteht begründeter Verdacht, dass der Produktionsprozess nicht mehr unter Kontrolle ist.

Beispiel 5.73 (Abstimmungen)

Eine Komitee bestehend aus \(n\) Personen stimmt in einer geheimen Abstimmung über ein vorgelegtes Projekt ab. Erfolg \(S\) ist die Zustimmung einer Person, \(F\) die Ablehnung. \(S_n\) ist die Anzahl der für das Projekt abgegebenen Stimmen. Wie wahrscheinlich ist eine Mehrheit für das Projekt?

Beispiel 5.74 (No-shows im Tourismus)

Ein Flugzeug mit \(n\) Sitzplätzen ist ausgebucht. Aus Erfahrung wissen die Manager der Airline, dass ein Prozentsatz \(p\) von Fluggästen trotz Buchung nicht erscheinen wird, sgn. no-shows. Wenn die Wahrscheinlichkeitsverteilung von \(S_n\), der Anzahl der no-shows bekannt ist, kann gezielt überbucht werden, um die Auslastung des Flugzeugs zu verbessern.

5.5.2 Verteilung der Anzahl der Erfolge

Satz 5.75 (Binomialverteilung) Die Zufallsgröße \(S_n\), die Anzahl der Erfolge in einer Serie von \(n\) Bernoulli-Experimenten, ist binomialverteilt mit: \[ \begin{gathered} P(S_n=k)=\binom{n}{k}p^k(1-p)^{n-k},\quad k=0,1,\ldots,n, \end{gathered} \tag{5.33}\] dabei bezeichnet \(\binom{n}{k}\) den Binomialkoeffizienten: \[ \begin{gathered} \binom{n}{k}=\frac{n(n-1)(n-2)\cdots(n-k+1)}{k!}=\frac{n!}{k!(n-k)!}. \end{gathered} \] Erwartungswert und Varianz von \(S_n\) sind: \[ \begin{gathered} E(S_n)=np,\quad V(S_n)=np(1-p). \end{gathered} \tag{5.34}\]

Begründung: Wenn das Ereignis \(\{S_n=k\}\) eintritt, müssen in der Serie von \(n\) Experimenten genau \(k\) Erfolge \(S\) und \(n-k\) Misserfolge \(F\) auftreten. Eine Serie mit fixer Anordnung der Erfolge \(S\) hat daher Wahrscheinlichkeit \(p^k(1-p)^{n-k}\), wegen der Unabhängigkeit der Experimente.

Betrachten wir beispielsweise eine Versuchsfolge der Länge \(n=5\) mit den Ergebnissen (in der angegeben Reihenfolge): \[ \begin{gathered} \mathit{SFFSF}\implies P(\mathit{SFFSF})=p^2(1-p)^3. \end{gathered} \] Allerdings haben auch die Folgen SSFFF, FFFSS und noch sieben weitere Folgen die gleiche Wahrscheinlichkeit \(p^2(1-p)^3\). Hier kommt der Binomialkoeffizient ins Spiel: \[ \begin{gathered} \binom{n}{k}=\begin{array}{l} \text{Anzahl der Möglichkeiten, den $k$ Erfolgen $S$}\\ \text{Plätze in einer Serie der Länge $n$ zuzuordnen} \end{array} \end{gathered} \] Das ist einfach zu erklären: eine Liste von \(n\) Objekten kann auf \[ \begin{gathered} n!=1\cdot 2\cdot 3\cdots n \end{gathered} \] unterschiedliche Arten angeordnet (permutiert) werden. Unsere Objekte sind allerdings nur von zweierlei Art, nämlich \(S\) und \(F\), wobei die \(S\) und die \(F\) nicht untereinander unterscheidbar sind. Das bedeutet, dass die \(k!\) Permutationen der \(S\) alle die gleiche Konfiguration ergeben, ebenso sind alle \((n-k)!\) Permutationen der Misserfolge \(F\) ununterscheidbar. Um diese beiden Faktoren vermindert sich somit die Anzahl der Permutationen. Daher ist die Anzahl der Möglichkeiten, den Erfolgen und Misserfolgen Plätze in der Versuchsreihe zuzuweisen: \[ \begin{gathered} \frac{n!}{k!(n-k)!}=\binom{n}{k}, \end{gathered} \] damit ist (5.33) gezeigt. Um Erwartungswert und Varianz zu finden, verwenden wir am besten Indikatorgrößen: \[ \begin{gathered} X_i=\left\{\begin{array}{cl} 1 & \text{wenn $i$-ter Versuch Erfolg $S$}\\[4pt] 0 & \text{wenn $i$-ter Versuch Misserfolg $F$} \end{array} \right.,\quad i=1,2,\ldots,n \end{gathered} \] Wegen (5.20) ist für \(i=1,2,\ldots,n\); \[ \begin{gathered} E(X_i)=1\cdot p+0\cdot(1-p)=p,\quad E(X_i^2)=1^2\cdot p+0^2(1-p)=p, \end{gathered} \] und wegen des Verschiebungssatzes (Satz 5.50): \[ \begin{gathered} V(X_i)=p-p^2=p(1-p). \end{gathered} \] Nun ist aber \(S_n=X_1+X_2+\ldots+X_n\). Wegen der Linearität des Erwartungswerts (Satz 5.40): \[ \begin{aligned} E(S_n)&=E(X_1+X_2+\ldots+X_n)\\ &=E(X_1)+E(X_2)+\ldots+E(X_n)\\ &=np. \end{aligned} \] Und weil die \(X_i\) unabhängige Zufallsgrößen sind, ist das Additionsgesetz (Satz 5.56) anwendbar: \[ \begin{aligned} V(S_n)&=V(X_1+X_2+\ldots+X_n)\\ &=V(X_1)+\ldots+V(X_n)\\ &=np(1-p). \end{aligned} \] □

Abbildung 5.12 zeigt die Wahrscheinlichkeitsfunktion (5.33) der Binomialverteilung für \(n=10\) und verschiedene Werte der Erfolgswahrscheinlichkeit \(p\).

Abbildung 5.12: Binomialverteilung für \(n=10\) und verschiedene \(p\).

Musteraufgabe 5.76 (Statistische Prozesskontrolle) Ein Produktionsprozess gilt als unter Kontrolle, wenn er mit einer Ausschussrate von maximal 1.5 % arbeitet. Um das zu überprüfen, wird aus der laufenden Produktion eine Stichprobe der Größe \(n=10\) gezogen und die ausgewählten Items auf Einhaltung der Qualitätsstandards überprüft. Dabei zeigte sich, dass zwei kontrollierte Items nicht entsprachen.

Wie wahrscheinlich ist es, mindestens zwei unbrauchbare Items in der Stichprobe zu finden, wenn der Prozess unter Kontrolle ist?

Lösung: Wir definieren Erfolg \(S\) als das Ereignis {kontrollierter Item entspricht nicht den Vorgaben}. Wenn der Prozess unter Kontrolle ist, dann beträgt die Erfolgswahrscheinlichkeit \(p=0.015\). Es sei \(S_{10}\) die Anzahl der unbrauchbaren Items in einer Stichprobe der Größe \(n=10\).

Wir suchen \(P(S_{10}\ge 2)\). Mittels (5.33): \[ \begin{aligned} &P(S_{10}\ge 2)\\ &=1 - P(S_{10}\le 1)\\[4pt] &=1-\left[P(S_{10}=0)+P(S_{10}=1)\right]\\[4pt] &=1-\left[\binom{10}{0}0.015^0(1-0.015)^{10}+\binom{10}{1} 0.015^1(1-0.015)^{9}\right]\\[4pt] &=1-\left[0.85973 + 0.13092\right]=0.00935\,. \end{aligned} \] Es ist also sehr unwahrscheinlich, zwei oder mehr defekte Items in einer 10-er Stichprobe zu finden, wenn der Prozess mit Ausschussrate 1.5% läuft. Dieses Ergebnis ist somit ein starkes Indiz dafür, dass die Hypothese \(p=0.015\) nicht länger aufrecht erhalten werden kann. □

Musteraufgabe 5.77 (Abstimmungsverhalten) Der fünfköpfige Vorstand eines Vereins muss kurzfristig über einen Antrag eines Vereinsmitglieds abstimmen.

1. Wenn die Vorstandsmitglieder völlig indifferent und unentschlossen sind (Zustimmungswahrscheinlichkeit \(p=0.5\)), mit welcher Wahrscheinlichkeit findet der Antrag eine Mehrheit?

2. Vier der Vorstandsmitglieder sind indifferent (\(p=0.5\)), ein Mitglied des Vorstands ist aber definitiv gegen den Antrag. Wie wahrscheinlich ist es nun, dass der Antrag mit Mehrheit angenommen wird?

Es wird angenommen, dass geheim abgestimmt wird und damit Unabhängigkeit gewährleistet ist.

Lösung:

(a) Es sei \(S_5\) die Anzahl der Stimmen für den Antrag. Dieser wird mehrheitlich angenommen, wenn \(S_5\ge 3\) ist: \[ \begin{aligned} P(S_5\ge 3)&=P(S_5=3)+P(S_5=4)+P(S_5=5)\\[5pt] &=\binom{5}{3}0.5^5+\binom{5}{4}0.5^5+\binom{5}{5}0.5^5\\[5pt] &=0.312500 + 0.156250 + 0.031250 = 0.5\,. \end{aligned} \] Wie zu erwarten hat der Antrag eine fifty-fifty Chance angenommen zu werden.

(b) Da jetzt einer definitiv gegen den Antrag stimmen wird, müssen von den vier Verbleibenden mindestens drei für den Antrag stimmen: \[ \begin{aligned} P(S_4\ge 3)&=P(S_4=3)+P(S_4=4)\\[5pt] &=\binom{4}{3}0.5^4+\binom{4}{4}0.5^4=0.25+0.0625=0.3125\,. \end{aligned} \] Die Chancen des Antrags sind nun deutlich gesunken. □

Musteraufgabe 5.78 Der Intelligenzquotient sei normalverteilt mit \(\mu=100\) und \(\sigma=15\). Ein Kind gilt als hochbegabt, wenn es bei einem Test einen IQ von über 130 erzielt. Eine Schulklasse mit 20 Kindern wird getestet. Wir wahrscheinlich ist es, dass in dieser Klasse mehr als ein hochbegabtes Kind zu finden ist?

Lösung: Wir berechnen zuerst die Wahrscheinlichkeit, dass der Intelligenzquotient \(Q>130\) ist: \[ \begin{aligned} P(Q>130)&=1-P(Q\le130)\\ &=1-\Phi\left(\frac{130-100}{15}\right)=1-\Phi(2)=0.023\,. \end{aligned} \] Ein Kind der Klasse kann nun hochbegabt sein (Erfolg) mit Wahrscheinlichkeit \(0.023\) oder es ist nicht hochbegabt. Unabhängigkeit vorausgesetzt ist die Anzahl der Hochbegabten in der Klasse binomialverteilt mit \(n=20\) und \(p=0.023\). Wir suchen \(P(S_{20}>1)\): \[ \begin{aligned} P(S_{20}>1)&=1-P(S_{20}\le 1)\\[5pt] &=1-\left[P(S_{20}=0)+P(S_{20}=1)\right]\\[5pt] &=1-\left[\binom{20}{0}0.023^0\cdot 0.977^{20}+\binom{20}{1}0.023^1\cdot 0.977^{19}\right]\\[5pt] &=1-[0.62790 + 0.29563]=0.07647\,. \end{aligned} \] □

5.5.3 Approximation durch die Normalverteilung

Die Berechnung von Wahrscheinlichkeiten der Binomialverteilung ist oft sehr mühsam, vor allem weil die Binomialkoeffizienten extrem große Zahlen werden, selbst für moderate Werte von \(n\). Da aber die Zufallsgröße \(S_n\) als Summe von unabhängigen Zufallsgrößen darstellbar ist (siehe Formeln bei Abbildung 5.12), kann man den zentralen Grenzwertsatz, dh. eine Näherung durch die Normalverteilung, nutzen.

Genauer: wir approximieren die Verteilungsfunktion von \(S_n\), d.h. die Wahrscheinlichkeit \(P(S_n\le k)\), durch die Verteilungsfunktion einer Zufallsgröße \(X\), die normalverteilt ist mit Mittelwert und Varianz, wie wir sie in Satz 5.75 gefunden haben, nämlich: \[ \begin{gathered} \mu=np,\quad \sigma^2=np(1-p). \end{gathered} \] Um die Genauigkeit zu erhöhen, ist es zweckmäßig eine Stetigkeitskorrektur von \(0.5\) zu \(k\) zu addieren, sodass: \[ \begin{gathered} P(S_n\le k)\approx P(X\le k+0.5)=\Phi\left(\frac{k+0.5-\mu}{\sigma}\right). \end{gathered} \tag{5.35}\] Diese Approximation liefert in der Regel schon dann recht brauchbare Werte, wenn die Varianz \(\sigma^2>9\) ist.

Musteraufgabe 5.79 Eine Fluglinie setzt auf vielen ihrer Strecken Flugzeuge des Typs A320-200 ein, die über ein Platzangebot von 180 Sitzen verfügen. Aus Erfahrung ist bekannt, dass 7.5% der Passagiere trotz gültigen Tickets nicht zum Abflug erscheinen, sgn. no-shows.

1. Wie wahrscheinlich ist es, dass bei ausgebuchter Maschine mehr als 10 Plätze frei bleiben?

2. Mit wievielen Plätzen darf der Flug überbucht werden, sodass mit Wahrscheinlichkeit 99 % kein Fluggast mit gültigem Ticket abgewiesen werden muss?

Lösung:

(a) Die Anzahl \(S_n\) von no-shows unter \(n\) Buchungen ist binomialverteilt mit \(p=0.075\). Für \(n=180\) errechnen wir zuerst: \[ \begin{gathered} \mu=180\cdot 0.075=13.5,\quad \sigma^2=180\cdot 0.075\cdot0.925=12.4875>9. \end{gathered} \] Da die Varianz \(\sigma^2>9\) ist, erwarten wir eine Approximation von akzeptabler Genauigkeit: \[ \begin{aligned} P(S_{180}>10)&=1-P(S_{180}\le 10)\approx 1-\Phi\left(\frac{10+0.5-13.5}{\sqrt{12.4875}} \right)\\[5pt] &=1-\Phi(-0.85)=1-0.198=0.802\,. \end{aligned} \] Der exakte Wert dieser Wahrscheinlichkeit, errechnet mit einem Computer Programm, ist \(P(S_{180}>10)=0.79911\). Der Approximationsfehler beträgt nur 0.0029 !

(b) Es sei \(m\) die Anzahl der über das Limit 180 verkauften Tickets. Dann ist die Gesamtzahl der Buchungen \(N=180+m\). Wieder sei \(S_N\) die Anzahl der no-shows. Das Ereignis {kein Fluggast muss abgewiesen werden} kann nur eintreten, wenn \(S_N\ge m\), denn dann ist die Zahl der no-shows wenigstens so groß wie die Zahl der Überbuchungen. Dieses \(S_N\) ist approximativ normalverteilt mit Erwartungswert \[ \begin{gathered} \mu=Np=(180+m)\cdot 0.075=13.5+0.075m \end{gathered} \] und Varianz \[ \begin{aligned} \sigma^2&=Np(1-p)=(180+m)\cdot 0.0.75\cdot(1-0.075)\\[5pt] &=12.487500 + 0.069375 m. \end{aligned} \] Nun formulieren wir eine Gleichung für das unbekannte \(m\) aus der Forderung \(P(S_N\ge m)=0.99\): \[ \begin{gathered} P(S_N\ge m)=1-P(S_N\le m-1)=0.99\\[5pt] \implies P(S_N\le m-1)=0.01\,. \end{gathered} \] Jetzt die Approximation mit dem zentralen Grenzwertsatz: \[ \begin{gathered} P(S_N\le m-1)\approx\Phi\left(\frac{m-1+0.5-(13.5+0.075m)}{ \sqrt{12.4875 + 0.069375 m}}\right)=0.01\\[5pt] \frac{0.925 m - 14}{\sqrt{12.4875 + 0.069375\, m}}=\Phi^{-1}(0.01)=-2.3263\\[5pt] 0.925 m - 14=-2.3263\sqrt{12.4875 + 0.069375\, m}\,. \end{gathered} \] Um die Wurzel loszuwerden quadrieren wir beide Seiten der Gleichung, bedenken dabei aber, dass Quadrieren keine Äquivalenztransformation ist. Tatsächlich erhalten wir (nach Vereinfachung) die quadratische Gleichung: \[ \begin{gathered} 0.855625 \,m^2 - 26.27543472\, m + 128.4217498=0. \end{gathered} \] Sie besitzt die beiden Lösungen: \[ \begin{gathered} m_1=6.10\simeq 6,\quad m_2=24.61\simeq 25. \end{gathered} \] Wir nehmen die Lösung \(m=6\) und damit akzeptieren wir \(N=186\) Buchungen.

Sie können leicht nachrechnen, dass bei \(N=180+25=205\) Buchungen mit Wahrscheinlichkeit 99% mindestens ein Fluggast abgewiesen werden müsste. □

5.6 Weitere Übungsaufgaben

1. Ein Spieler beteiligt sich an einem symmetrischen Glücksspiel. Es sei \(W\) die Wartezeit (Anzahl der Einzelspiele) bis zum ersten Gewinn. Man berechne \(P(3<W\le 8)\).

   Lösung: \(P(3<W\le 8)=P(S_3=0)-P(S_8=0)=0.1211\)

2. Ein Würfel wird viermal geworfen, wie wahrscheinlich ist es mindestens einmal eine Sechs zu werfen? Zwei Würfel werden 24 mal geworfen, wie wahrscheinlich ist es, mindestens eine Doppelsechs zu werfen?

   Lösung: \(0.5177>0.4914\), De Méré’s Paradox (1654)

3. Eine Familie hat zwei Kinder. Es ist bekannt, dass eines davon ein Mädchen ist. Mit welcher Wahrscheinlichkeit sind beide Kinder Mädchen?

   Lösung: \(1/3\)

4. Man weiß aus Umfragen, dass 40 Prozent der Fernsehzuschauer regelmäßig die Nachrichtensendung ZIB 2 sehen und 80 Prozent die ZIB 1. 90 Prozent der Zuschauer sehen wenigstens eine der beiden Sendungen. Wie groß ist die Wahrscheinlichkeit, dass ein zufällig ausgewählter Zuschauer sich beide Sendungen ansieht?

   Lösung: 0.3

5. In einer technischen Untersuchung werden an PKWs folgende Ereignisse erhoben: \(R=\){Der PKW weist Rostschäden auf} und \(S=\){Der PKW wird mit dem Markenprodukt XY gepflegt}. Es stellt sich heraus, dass \(P(R) = 0.37\) und \(P(S) = 0.71\). Außerdem ist \(P(R\cap S) = 0.11\).

   1. Man bestimme die Wahrscheinlichkeit, dass ein mit XY gepflegtes Fahrzeug Rostschäden besitzt.

   2. Man bestimme die Wahrscheinlichkeit, dass ein Fahrzeug mit Rostschäden mit XY gepflegt wird.

   3. Man bestimme die Wahrscheinlichkeit, dass ein Fahrzeug ohne Rostschäden mit XY gepflegt wird.

   4. Man bestimme die Wahrscheinlichkeit, dass ein Fahrzeug mit Rostschäden nicht mit XY gepflegt wird.

   Lösung:

   (a) \(P(R|S)=0.1549\), (b) \(P(S|R)=0.2973\), (c) \(P(S|R')=0.9524\)
   (d) \(P(S'|R)=0.7027\)

6. Eine Umfrage ergab, dass 18 Prozent aller Studenten männlichen Geschlechts sind und rauchen. 42 Prozent aller Studenten rauchen. 68 Prozent aller Nichtraucher unter den Studenten sind weiblichen Geschlechts.

   1. Wie groß ist die Wahrscheinlichkeit, dass eine Studentin raucht?

   2. Wie groß ist die Wahrscheinlichkeit, dass ein Student nicht raucht?

   Lösung: (a) \(P(R|W)=0.3783\), (b) \(P(R'|M)=0.5077\)

7. Im Jahr 2010 gehörten 19 von den 28 EU-Staaten dem Euro an. Von diesen wiederum haben lediglich vier die im Maastricht Vertrag festgelegte Defizitgrenze von 3% des BIP eingehalten. Von den 9 EU-Staaten, die nicht dem Euro angehörten, haben 7 die Defizitgrenze nicht eingehalten.

   1. Wieviel Prozent der Euroländer waren Maastricht-Sünder?

   2. Wieviel Prozent der Maastricht-Sünder waren Euro-Länder?

   3. Wie beurteilen Sie die Kopplung zwischen den Merkmalen \(E=\) {Mitglied in der Euro-Zone} und \(M=\) {Einhaltung der 3%-Grenze}?

   Lösung: (a) \(P(M'|E)=0.7895\), (b) \(P(E|M')=0.6818\), (c) \(E\) und \(M\) sind praktisch unabhängig.

8. In einem Unternehmen sind 40 Frauen und 75 Männer beschäftigt. 62 Mitarbeiter bzw. Mitarbeiterinnen verfügen über einen Studienabschluss, davon sind 25 weiblich.

   Welche der folgenden Aussagen sind richtig?

   1. 26.1 % der Mitarbeiter sind weiblich und haben einen Studienabschluss.

   2. 37.5 % der Frauen haben keinen Studienabschluss.

   3. 40.3 % der Mitarbeiter mit Studienabschluss sind weiblich.

   Lösung: Aussagen (2) und (3) sind richtig.

9. Für zwei Ereignisse \(A\) und \(B\), die bei einem Experiment beobachtet werden können, wurde folgende Vierfeldertafel ermittelt: \[ \begin{gathered} \begin{array}{l|cc|r} & A & A' &\\ \hline B & 0.40 & 0.10 & 0.50\\ B' & 0.20 & 0.30 & 0.50\\ \hline & 0.60 & 0.40 & \end{array} \end{gathered} \] Welche der folgenden Aussagen sind richtig?

   1. \(P(A\cap B)=0.40\)

   2. \(P(A'|B)=0.25\)

   3. \(P(A'|B')=0.60\)

   Lösung: Aussagen (1) und (3) sind richtig.

10. In Europa haben 9 % der Männer eine Rot-Grün Sehschwäche, aber nur 0.8 % der Frauen. Was ist der Anteil der Frauen an den Menschen mit Rot-Grün Sehschwäche (Bevölkerungsanteil der Frauen: 50%)?

    Lösung: 8.2 %

11. Eine diskrete Zufallsgröße \(X\) besitzt die Wahrscheinlichkeitsfunktion: \[ \begin{gathered} \begin{array}{c|ccccc} X & 0 & 1 & 2 & 3 & 4\\ \hline P(X=x) & 0.1 & 0.1 & 0.4 & 0.3 & 0.1 \end{array} \end{gathered} \] Berechnen Sie Erwartungswert und Varianz von \(X\).

    Lösung: \(\mu = 2.2 , \sigma^2= 1.16\)

12. Ein Unternehmen produziert mit linearer Kostenfunktion. Die variablen Kosten betragen 17 GE pro Stück, die Fixkosten eine Mio. GE pro Monat. Dabei ist die monatliche Produktionsmenge \(X\) eine Zufallsgröße mit Erwartungswert 21 000 Stück. Der erzielbare Marktpreis \(P\) ist ebenfalls eine Zufallsgröße, unabhängig von \(X\), mit \(E(P)=80\) GE. Berechnen Sie den erwarteten monatlichen Gewinn, unter der Annahme, dass die gesamte Produktion verkauft werden kann.

    Lösung: \(323\,000\)

13. Eine Investorin bildet ein Portfolio, in das sie vier Wertpapiere \(A,B,C,D\) hineinnimmt mit Kapitalanteilen von 25 %, 40 %, 10 % und 25 %. Die Renditen dieser Wertpapiere sind unabhängige Zufallsgrößen. Von diesen vier Papieren kennt sie die erwarteten Renditen und die Standardabweichungen der Renditen. \[ \begin{gathered} \begin{array}{c|cccc} & A & B & C & D\\ \hline E(R_i) & 0.08 & 0.12 & 0.06 & 0.09\\ \sigma(R_i) & 0.06 & 0.09 & 0.01 & 0.08 \end{array} \end{gathered} \] Berechnen Sie die erwartete gemeinsame Rendite des Portfolios und deren Standardabweichung.

    Lösung: \(E(R)=0.0965\), \(\sigma(R)=0.0438\)

14. Ein Investor möchte ein Portfolio bilden, das ihm minimales Risiko garantiert. 10 % des Kapitals sollen dabei risikofrei investiert werden in Wertpapier \(C\), das vertraglich garantiert 6 % Rendite bringt. Das übrige Kapital soll auf zwei Wertpapiere \(A\) und \(B\) optimal verteilt werden. Folgende Daten stehen zur Verfügung: \[ \begin{gathered} \begin{array}{c|ccc} & A & B & C\\ \hline E(R_i) & 0.14 & 0.16 & 0.06\\ \sigma(R_i) & 0.08 & 0.09 & 0.00 \end{array} \end{gathered} \] Die Renditen von \(A\) und \(B\) sind unabhängige Zufallsgrößen. Was sind die Kapitalanteile von \(A\) und \(B\) im optimalen Portfolio, was ist die erwartete gemeinsame Rendite?

    Lösung: Anteil \(A\) : 50.3 %, Anteil \(B\): 39.7 %, \(E(R)=0.14\).

15. Eine Handelsfirma produziert Packungen mit Kaffeebohnen, deren Abfüllgewicht den Erwartungswert \(\mu=250\) \(g\) und die Standardabweichung \(\sigma=16\) \(g\) hat. Bei der Qualitätskontrolle werden Kartons mit jeweils 8 Packungen gewogen. Wie groß sind Erwartungswert und Standardabweichung des durchschnittlichen Gewichts einer Packung in einem Karton?

    Lösung: \(E(\overline{X})=E(X)=250\), \(\sigma(\overline{X})=\sqrt{32}=5.6569\)

16. Der Benzinverbrauch von PKW (in Liter, pro 100 km) sei normalverteilt mit Mittelwert 8.2 und Varianz 2.4.

    1. Wie groß ist der Anteil der PKW, die mehr als 10 Liter verbrauchen?

    2. Welcher Verbrauch wird von 25 Prozent der PKW überschritten?

    Lösung: (a) \(P(X>10)=0.123\), (b) 9.24 Liter/100 km.

17. Die Betriebsdauer eines Gerätes bis zum 1. Ausfall (in Monaten) ist normalverteilt mit \(\mu = 24.15\) und \(\sigma^2 = 121\). Ein Händler garantiert, das Gerät zu ersetzen, wenn es innerhalb der ersten 6 Monate ausfällt. Wieviele Garantiefälle sind bei 6000 Geräten zu erwarten?

    Lösung: 294

18. Auf einem unfallträchtigen Autobahnteilstück wurden umfangreiche Radarmessungen der Geschwindigkeiten durchgeführt. Dabei ergab sich, dass die gefahrenen Geschwindigkeiten in guter Näherung normalverteilt sind mit Mittelwert 95 km/h und Standardabweichung 12 km/h. Aus Gründen der Verkehrssicherheit besteht auf der Strecke ein Tempolimit von 100 km/h. Was ist der Anteil der Fahrzeuge, die das Tempolimit überschreiten? Welche Geschwindigkeit wird von 1 % der Fahrzeuge überschritten?

    Lösung: \(0.337\), \(123\) km/h

19. In der Fertigpackungsverordnung 1993 (FPVO) wird in § (1) festgelegt, dass bei Behältnissen mit einem Nennfüllvolumen von 500 Milliliter die Abweichung von diesem Wert maximal \(\pm\) 2 % des Volumens betragen darf. Angenommen, die Füllmengen einer Abfüllanlage sind normalverteilt mit Erwartungswert 500 ml und Standardabweichung 3.8 ml. Mit welcher Wahrscheinlichkeit werden die Vorgaben der FPVO eingehalten?

    Lösung: \(0.992\)

20. Vor der Kassa eines Kinos hat sich eine Warteschlange gebildet, Herr A steht an der 21. Stelle. Die Zeit, die ein Besucher an der Kassa braucht, um seine Eintrittskarte zu kaufen, ist eine Zufallsgröße mit Erwartungswert 63 Sekunden und Standardabweichung 60 Sekunden. Die Wartezeit von A ist die Summe der Bedienzeiten aller Besucher vor ihm in der Schlange. Wie wahrscheinlich ist es, dass A länger als eine halbe Stunde warten muss? Approximieren Sie diese Wahrscheinlichkeit mit Hilfe des zentralen Grenzwertsatzes.

    Lösung: \(0.022\)

21. Ein Verkehrsflugzeug verfügt über vier Triebwerke. Die Wahrscheinlichkeit, dass ein Triebwerk während eines Transatlantikfluges ausfällt oder wegen technischer Probleme abgeschaltet werden muss, ist \(0.001\). Wie wahrscheinlich ist es, dass während eines Transatlantikfluges zwei oder mehr Triebwerke ausfallen?

    Lösung: \(0.000005992\)

22. Die Wahrscheinlichkeit eines schweren Unfalls betrage bei einem technischen Verfahren 1:10 000 im Laufe eines Jahres. Wie groß ist die Wahrscheinlichkeit dafür, dass beim Betrieb von 30 Anlagen im Laufe von 10 Jahren der Unfall mindestens einmal auftritt?

    Lösung: \(0.0296\)

23. Ein Bankunternehmen weiß, dass 18 Prozent der privaten Kreditnehmer die Überziehung des Gehaltskontos als Finanzierungsform wählen, obwohl dafür Zinsen von 13 % pro Jahr berechnet werden. Wie groß ist die Wahrscheinlichkeit, dass von 8 zufällig ausgewählten Kunden mindestens einer das Gehaltskonto überzieht?

    Lösung: \(0.7956\)

24. Eine Wiener Familie baut ihr Wochenendhaus in romantischer Lage an einem Fluss. Der Fluss wurde seinerzeit so reguliert, dass er mit der Wahrscheinlichkeit 0.06 innerhalb eines Jahres über die Ufer tritt.

    1. Wie wahrscheinlich ist es, in den nächsten 20 Jahren genau 3 Jahre mit Überschwemmungen zu erleben.

    2. Wie wahrscheinlich ist es, in den nächsten 20 Jahren höchstens 3 Jahre mit Überschwemmungen zu erleben.

    Lösung: (a) \(0.086\), (b) \(0.971\)

25. Die Partei Grüne erreichte bei der Nationalratswahl 2017 einen Stimmenanteil von 3.8 %. Im Rahmen einer Analyse nach der Wahl wird eine Zufallsstichprobe gezogen. Wie groß muss der Umfang der Stichprobe mindestens sein, damit sie mit einer Sicherheit von 99% wenigstens einen Grün-Wähler enthält?

    Lösung: \(n\ge 119\)

26. Die Servicezeit \(T\) (Scannen der Waren, Bezahlvorgang) eines Kunden bei einer Kassa in einem Supermarkt ist exponentialverteilt mit \(P(T>t)=e^{-0.0125t}\) (Zeit in Sekunden). Wie wahrscheinlich ist es, dass von 10 zufällig ausgewählten Kunden maximal drei länger als zwei Minuten an der Kassa verbringen?

    Lösung: \(0.835\)

27. Ein Produktionsprozess läuft unter idealen Bedingungen mit einer Ausschussrate von 2.2 %. Zu Zwecken der Qualitätskontrolle werden in gewissen Zeitabständen aus der laufenden Produktion Stichproben der Größe \(n=20\) gezogen und die Produkte auf ihre Qualität überprüft. Die Werkmeisterin hat den Auftrag, den Prozess anzuhalten, wenn von den 20 kontrollierten Items mehr als zwei Ausschussware sind.

    1. Wie wahrscheinlich ist es, dass der Prozess angehalten wird, wenn die Maschine mit Ausschussrate 2.2 % arbeitet?

    2. Wie wahrscheinlich ist dieses Ereignis, wenn durch eine Störung die Ausschussrate tatsächlich auf 8 % gestiegen ist?

    Lösung: (a) \(0.0092\), (b) \(0.2121\)

---

1. Jakob I. Bernoulli (1655–1705), Schweizer Mathematiker und Physiker mit wichtigen Beiträgen zur Wahrscheinlichkeitstheorie. Von ihm stammt eine erste Form des Gesetzes der großen Zahlen.