1 Lineare und quadratische Funktionen
1.1 Lineare Funktionen
Unter den reellen Funktionen sind die linearen die einfachsten. Ihre Bedeutung ist aber nicht allein ihrer Einfachheit geschuldet. Lineare Funktionen werden oft auch dazu verwendet, komplizierte Funktionen zu approximieren.
1.1.1 Funktionsterme
Definition 1.1 Funktionen \(f:\mathbb R \rightarrow \mathbb R\) mit einem Funktionsterm der Form \(f(x)=kx\) oder \(f(x)=kx+d\) heißen lineare Funktionen.
Eine lineare Funktion hat als Definitionsbereich die Menge \(\mathbb R\) aller reellen Zahlen. Man unterscheidet zwischen homogenen linearen Funktionen mit dem Funktionsterm \(f(x)=kx\) und inhomogenen linearen Funktionen mit einem Funktionsterm \(f(x)=kx+d\), bei dem \(d\not=0\).
Die Funktionsterme \(f(x)=3x\), \(g(x)=-0.5x\), \(h(x)=4.37x\) definieren homogene lineare Funktionen. Der Funktionsterm \(s(x)=-7x+2\) definiert eine inhomogene lineare Funktion.
1.1.2 Funktionsgraphen
Wie sieht der Funktionsgraph von linearen Funktionen aus? Was ist das Besondere an den Graphen von linearen Funktionen? Es wird sich herausstellen, dass die Funktionsgraphen von linearen Funktionen durch einen geradlinigen Verlauf gekennzeichnet sind.
Was aber heißt geradlinig? Anschaulich ist das völlig klar, aber worin äußert sich die Geradlinigkeit mathematisch am Funktionsterm einer linearen Funktion? Um diese Fragen zu beantworten, erinnern wir uns an den Begriff des Steigungsverhältnisses.
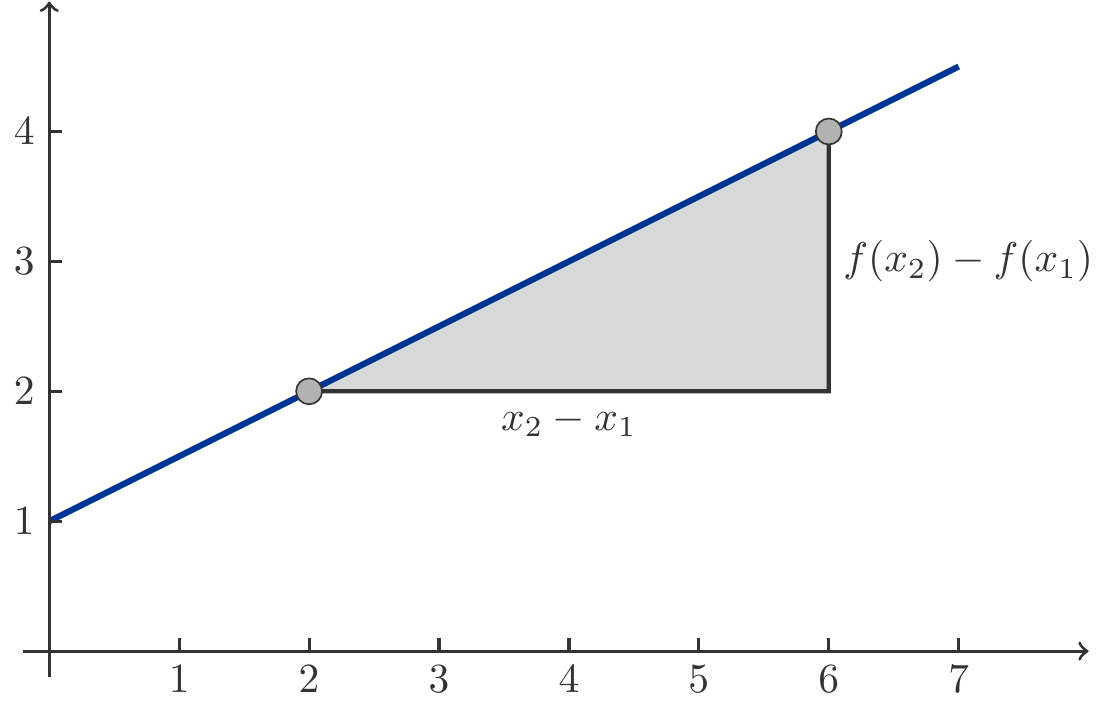
Bemerkung 1.3 (Steigungsverhältnis) Betrachten wir zunächst eine völlig beliebige reelle Funktion \(f\). Es seien \(x_1\) und \(x_2\) zwei Punkte der Definitionsmenge und \(f(x_1)\) bzw. \(f(x_2)\) seien die Werte der Funktion an diesen Punkten. Wie stark ändert sich die Funktion \(f\) beim Übergang der Variablen \(x\) von \(x_1\) nach \(x_2\)?
Eine erste Antwort besteht darin, die Differenz \(f(x_2)-f(x_1)\) anzugeben. Das ist tatsächlich die Änderung der Funktionswerte zwischen \(x_1\) und \(x_2\). Allerdings ist diese Größe kein sehr interessantes Maß für die Stärke der Veränderung, denn die Differenz hängt natürlich auch von der Schrittweite \(x_2-x_1\) ab. Um die Veränderungen der Funktion bei großen und kleinen Schritten fair miteinander vergleichen zu können, sollten wir eher die durchschnittliche Veränderung \[ \begin{gathered} \frac{f(x_2)-f(x_1)}{x_2-x_1} \end{gathered} \] heranziehen. Diese durchschnittliche Veränderung nennt man auch das Steigungsverhältnis oder den Differenzenquotienten der Funktion zwischen \(x_1\) und \(x_2\). Bei einer beliebigen reellen Funktion kann sich dieses Steigungsverhältnis natürlich ändern, wenn man die Punkte \(x_1\) und \(x_2\) ändert.

Es sei nun \(f(x)=kx+d\) eine lineare Funktion. Nimmt man zwei beliebige Zahlen \(x_1\) und \(x_2\) aus dem Definitionsbereich und berechnet man das Steigungsverhältnis zwischen diesen Punkten, dann erhält man (vgl. Abbildung 1.1) \[ \begin{gathered} \frac{f(x_2)-f(x_1)}{x_2-x_1}=\frac{(kx_2+d)-(kx_1+d)}{x_2-x_1}=k. \end{gathered} \tag{1.1}\]
Diese Gleichung bedeutet, dass das Steigungsverhältnis des Graphen einer linearen Funktion unabhängig von der Wahl der Zahlen \(x_1\) und \(x_2\) immer gleich groß ist. Am Funktionsgraphen äußert sich diese Eigenschaft dadurch, dass er einen geradlinigen Verlauf zeigt. Das konstante Steigungsverhältnis ist jene mathematische Eigenschaft, die für den geradlinigen Verlauf verantwortlich ist.
Eine lineare Funktion \(f(x)=kx+d\) hat zwei Parameter \(k\) und \(d\), die beide einen Einfluss auf das geometrische Erscheinungsbild des Funktionsgraphen haben. Wir wissen bereits aus (1.1), dass der Parameter \(k\) das Steigungsverhältnis, kurz die Steigung des Funktionsgraphen angibt. Die geometrische Bedeutung des Parameters \(d\) ist ebenso einfach zu sehen. Es ist \(f(0)=k\cdot 0 +d=d\). Also ist \(d\) der Funktionswert an der Stelle \(x=0\). Mit anderen Worten: Der Funktionsgraph der linearen Funktion \(f(x)=kx+d\) schneidet die senkrechte Koordinatenachse im Punkt \((0,d)\).
Bemerkung 1.4 (Geradengleichungen) Als Ergebnis unserer Überlegungen haben wir gesehen, dass der Funktionsgraph einer linearen Funktion stets eine Gerade ist. Allerdings ist die Umkehrung davon nicht richtig! Nicht jede Gerade ist der Funktionsgraph einer linearen Funktion. Es gibt ja auch Geraden, die senkrecht verlaufen. Solche Geraden haben kein Steigungsverhältnis und können daher nicht Funktionsgraphen von linearen Funktionen sein.
Beliebige Geraden werden in einem Koordinatensystem durch lineare Gleichungen der Form \(ax+by+c=0\) beschrieben. Eine allgemeine Gerade ist eine Punktmenge der Form \[ \begin{gathered} g=\{(x,y): ax+by+c=0\}. \end{gathered} \]
Wenn \(b\ne 0\) ist, dann ist die Gerade \(g\) ein Funktionsgraph. Wir können nämlich dann \(f(x):=y=-\frac{a}{b}x-\frac{c}{b}\) ausrechnen, die sgn. Normalform, und sehen so, dass \[ \begin{gathered} g=\{(x,y): ax+by+c=0\}=\{(x,y): y=f(x)\}, \end{gathered} \]
dass also \(g\) der Funktionsgraph einer linearen Funktion ist. Wenn aber \(b=0\) ist, dann definiert die Gleichung \(ax+c=0\) keine Funktion, denn es muss dann \(x=-\frac{c}{a}\) konstant sein und \(y\) darf jeden beliebigen Wert annehmen. Also erfüllt jedes Paar \((-\frac{c}{a},y)\) mit beliebigem \(y\in\mathbb R\) die Gleichung und der entsprechende Punkt liegt auf der Geraden, die nun senkrecht verläuft. Solche Geraden können nicht als Funktionsgraphen auftreten.
Bemerkung 1.5 (Berechnung der Parameter \(k\) und \(d\)) Wie viele Beispiele in diesem Kapitel zeigen werden, ist es eine immer wiederkehrende Aufgabe, die Parameter \(k\) und \(d\) aus geeigneten Informationen zu berechnen. Eine typische Situation ist folgende: es sind zwei Punkte \(P=(x_0,y_0)\) und \(Q=(x_1,y_1)\) gegeben, deren Koordinaten die Funktionsgleichung \(y=kx+d\) einer linearen Funktion erfüllen, wobei \(k\) und \(d\) unbekannt sind. Geometrisch betrachtet verläuft der Graph der Funktion durch die beiden Punkte \(P\) und \(Q\).
Wir gehen so vor: \(k\) ist das Steigungsverhältnis, also: \[ \begin{gathered} k=\frac{y_1-y_0}{x_1-x_0}=\frac{\Delta y}{\Delta x}, \end{gathered} \tag{1.2}\]
Aus der Gleichung \(y=kx+d\) ergibt sich unmittelbar \(d\), wenn wir den Punkt \(P\) oder \(Q\) einsetzen: \[ \begin{aligned} d &= y_0-k x_0=y_1-kx_1\;. \end{aligned} \tag{1.3}\]
Musteraufgabe 1.6 Bestimmen Sie die Funktionsgleichung jener linearen Funktion, deren Graph durch die Punkte \(P=(3,8)\) und \(Q=(7,4)\) verläuft.
Lösung: Aus (1.2) und (1.3) ergibt sich: \[ \begin{gathered} k=\frac{4-8}{7-3}=-1,\quad d=8-(-1)\cdot 3=11\;. \end{gathered} \] Daher ist \(y=-x+11\). □
1.1.3 Kosten und Erlöse
Wir besprechen nun einige wirtschaftliche Anwendungen von linearen Funktionen. Bei diesen Beispielen zeigt sich, dass der mathematisch maximal mögliche Definitionsbereich einer linearen Funktion meist nicht identisch ist mit dem Definitionsbereich, auf dem die Funktion eine wirtschaftlich sinnvolle Interpretation besitzt. Meist sind nur nichtnegative Werte \(x\ge 0\) im wirtschaftlichen Zusammenhang sinnvoll.
Lineare Kostenfunktionen
In vielen Bereichen entstehen Kosten, die eine lineare Funktion der verbrauchten Menge irgendwelcher Ressourcen sind.
Die Kosten, die ein Haushalt für den Verbrauch an elektrischem Strom zu entrichten hat, sind eine lineare Funktion der verbrauchten Strommenge (gemessen in Kilowattstunden). Diese lineare Kostenfunktion \(C(x)=kx+d\) setzt sich zusammen aus dem Grundpreis \(d\), dem Tarifpreis \(k\) für eine Kilowattstunde und der verbrauchten Menge \(x\).
Für jemanden, der über keinen Vertrag mit großzügiger Flat Rate verfügt, sind die Telefonkosten pro Monat eine lineare Funktion der verbrauchten Gesprächsminuten. Diese lineare Kostenfunktion \(C(x)=kx+d\) setzt sich zusammen aus der monatlichen Grundgebühr \(d\), dem Tarifpreis \(k\) für eine Minute und der Anzahl \(x\) von Gesprächsminuten pro Monat.
Auch bei der Produktion von Gütern sind lineare Kostenfunktionen ein einfaches, aber wichtiges mathematisches Modell. Es sei \(C(x)=kx+d\) eine beliebige lineare Kostenfunktion, wobei \(x\) die produzierte Gütermenge angibt. Dann sind \(C(0)=d\) die Fixkosten, die auch dann anfallen, wenn nicht produziert wird. Die variablen Kosten betragen somit \(V(x)=C(x)-C(0)=kx\). Das sind die mengenabhängigen Kosten.
Wie hoch sind die Produktionskosten einer Mengeneinheit (Stückkosten), wenn eine lineare Kostenfunktion vorliegt?
Diese Frage besitzt zwei unterschiedliche Antworten je nachdem, was man unter den Produktionskosten einer Mengeneinheit versteht. Eine mögliche Interpretation versteht unter den Stückkosten die durchschnittlichen Kosten \[ \begin{gathered} \overline{C}(x)=\frac{C(x)}{x}, \end{gathered} \] die durch Produktion einer Mengeneinheit verursacht werden. Bei einer linearen Kostenfunktion betragen die durchschnittlichen Kosten \[ \begin{gathered} \overline{C}(x)=\frac{C(x)}{x}=\frac{kx+d}{x}=k+\frac{d}{x}. \end{gathered} \] \(\overline{C}(x)\) ist freilich keine lineare Funktion mehr (siehe Abbildung 1.2).
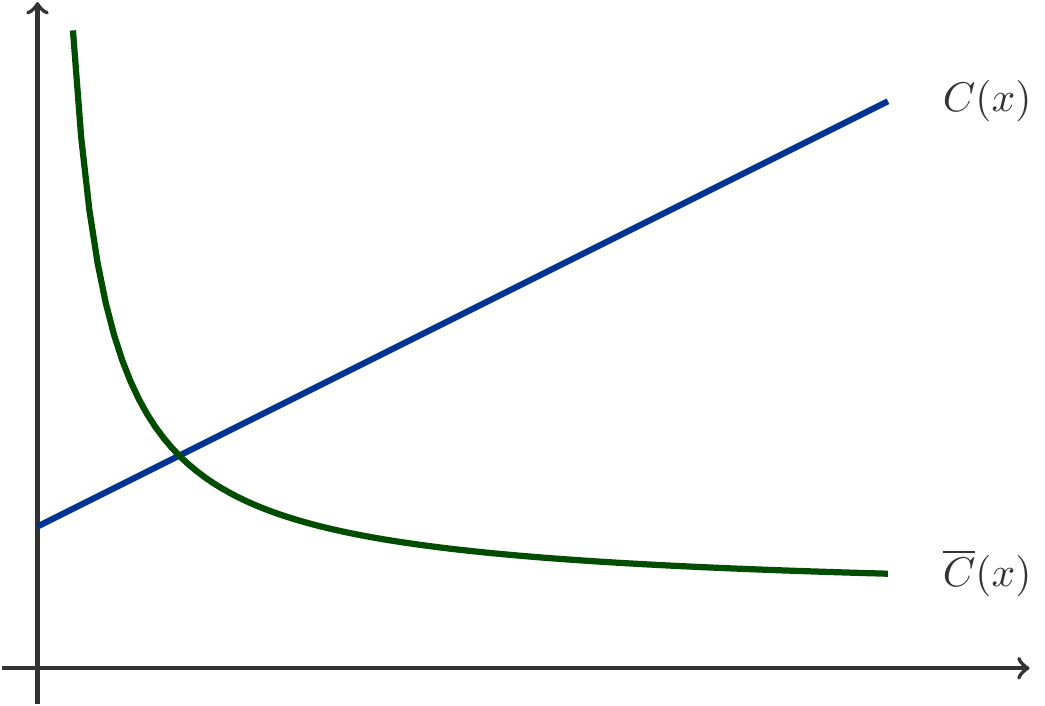
Die durchschnittlichen Kosten enthalten also einen Anteil der Fixkosten \(d/x\), der mit wachsender Menge \(x\) immer geringer wird.
Eine andere mögliche Interpretation von Stückkosten meint jene Kosten, die durch die Produktion einer weiteren Mengeneinheit verursacht werden. Produzieren wir also beispielsweise die Menge \(x\) und wollen wir eine weitere Mengeneinheit produzieren, dann verursacht dies zusätzliche Kosten in der Höhe \(C(x+1)-C(x)\). Diese Mehrkosten einer zusätzlichen Mengeneinheit nennt man auch marginale Kosten. Die marginalen Kosten betragen bei einer linearen Kostenfunktion \[ \begin{gathered} C(x+1)-C(x)=k(x+1)+d-(kx+d)=k. \end{gathered} \] Beim linearen Kostenmodell sind also die marginalen Kosten unabhängig davon, wie viel gerade produziert wird. Gleichgültig, ob wenig oder viel produziert wird, betragen die marginalen Kosten eines weiteren Stücks gleich viel. Bei einer höheren Produktion sinken die durchschnittlichen Kosten, während die marginalen Kosten immer gleich bleiben.
Sehen wir uns nun ein numerisches Beispiel an.
Musteraufgabe 1.7 Die Kostenfunktion laute \(C(x)=5x+3000\). Die momentane Produktion betrage \(x=10\,000\) Mengeneinheiten. Wie hoch sind die durchschnittlichen Stückkosten und wie hoch sind die marginalen Kosten?
Lösung: Die durchschnittlichen Kosten betragen \[ \begin{gathered} \overline{C}(10000)=\frac{C(10000)}{10000}= \frac{5\cdot 10000+3000}{10000}=5.3\;. \end{gathered} \] Dagegen betragen die marginalen Kosten genau \(5\). □
Die Eigenschaft, dass die marginalen Kosten konstant sind, ist kennzeichnend für eine lineare Kostenfunktion. Sie zeigt auch die Anwendungsgrenzen des linearen Kostenmodells. Der Verlauf der marginalen Kosten ist in der Praxis meist nicht konstant.
Erlösfunktionen
Der Verkaufspreis einer Mengeneinheit eines Gutes betrage \(p\). Mit \(x\) bezeichnen wir die verkaufte Menge. Dann beträgt der Erlös (englisch: revenue), der beim Verkauf der Menge \(x\) erzielt wird \[ \begin{gathered} R(x)=px. \end{gathered} \] Der Erlös ist also eine homogene lineare Funktion. Der Funktionsgraph ist eine Gerade, die durch den Punkt \((0,0)\) geht und die Steigung \(p\) besitzt.
Dass der Preis für die Marktteilnehmer eine gegebene Konstante ist, ist typisch für das Marktmodell der vollständigen Konkurrenz, auch Polypol genannt. In der Mikroökonomie versteht man darunter einen Markt, auf dem viele Anbieter vielen Nachfragern gegenüberstehen, so vielen jedenfalls, dass keiner der Marktteilnehmer über ausreichend Marktmacht verfügt, um durch autonome Aktionen den Marktpreis nachhaltig zu beeinflussen. Auf einem Monopolmarkt freilich sind die Verhältnisse völlig anders, wie wir in Abschnitt 1.2.2 sehen werden.
Rentabilität im linearen Kostenmodell
Es sei \(C(x)=kx+d\) eine lineare Kostenfunktion und \(R(x)=px\) sei die Erlösfunktion. Die Produktion ist rentabel, wenn der Erlös die Kosten übersteigt, dh. wenn \(R(x)>C(x)\). Im Fall \(R(x)<C(x)\) ist die Produktion unrentabel. Es ist wichtig, den Rentabilitätsbereich, dh. die Menge aller rentablen Produktionsmengen \(x\ge 0\) zu kennen.
Die Rentabilitätsbedingung lautet \(R(x)>C(x)\), dh. \(px>kx+d\) oder \[ \begin{gathered} (p-k)x>d. \end{gathered} \] Die Differenz \(p-k\) zwischen dem Preis und den marginalen Stückkosten nennt man den Deckungsbeitrag, der mit dem Produkt erzielt werden kann. Die Fixkosten \(d\) sind sicher nichtnegativ und auch die Produktionsmengen \(x\) sind nur als nichtnegative Zahlen sinnvoll. Die Rentabilitätsbedingung kann nur dann erfüllt werden, wenn der Deckungsbeitrag \(p-k>0\) positiv ist, also wenn \(p>k\) ist. Die Bedingung ist auch ökonomisch klar, denn eine rentable Produktion ist nur dann möglich, wenn der erzielbare Preis des Gutes die Stückkosten übersteigt.
Aber selbst dann, wenn \(p>k\), ist nicht jede Produktionsmenge rentabel. Die Rentabilitätsbedingung \((p-k)x>d\) besagt, dass die Menge \(x\) mindestens so groß sein muss, dass die Fixkosten \(d\) durch \((p-k)x\) zumindest ausgeglichen werden. Diese Mindestmenge, bei der ein Ausgleich der Fixkosten erfolgt, erhält man demnach, indem man die Gleichung \((p-k)x=d\) löst, und sie beträgt: \[ \begin{gathered} x_0=\frac{d}{p-k}=\frac{\text{Fixkosten}}{\text{Deckungsbeitrag}}. \end{gathered} \] Das ist die Gewinnschwelle oder der Break-even-Point.
Im allgemeinen erhält man den Break-even-Point \(x_0\) rechnerisch durch Lösen der Gleichung \(R(x)=C(x)\). Der daraus resultierende Rentabilitätsbereich lautet dann \(\{x:\;x>x_0\}=(x_0,\infty)\).
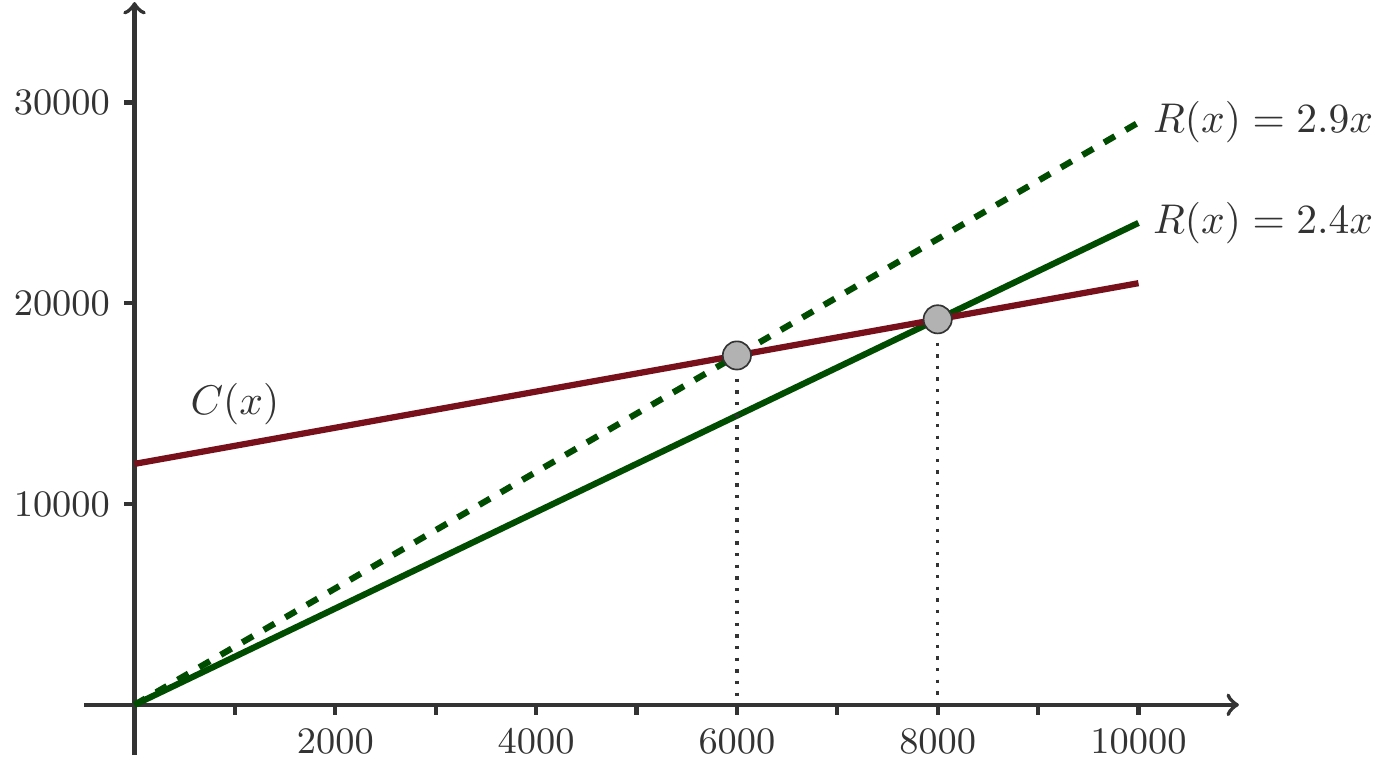
Musteraufgabe 1.8 Die Privatbrauerei Naturgold plant die Einführung eines neuen Produkts, eines Starkbiers, das unter dem Namen Favoritner Black Bock vertrieben werden soll. Lt. Planung werden die wöchentlichen Fixkosten der Produktion 12 000 GE betragen. Die variablen Kosten betragen pro Flasche Black Bock 0.9 GE, der Verkaufspreis wird mit 2.4 GE pro Flasche festgesetzt.
Wie lautet der Break-even-Point?
Wie müsste der Preis festgesetzt werden, damit der Break-even bei 6000 Flaschen erreicht wird?
Lösung: Aus dem Text der Angabe entnehmen wir die variablen Kosten pro Flasche \(k=0.9\) und die Fixkosten \(d=12\,000\). Daher lautet die Kostenfunktion: \(C(x) = 0.9x + 12\,000\). Die Erlösfunktion ist \(R(x)=p\cdot x=2.4 x\). Die Gewinnfunktion ergibt sich daraus als \[ \begin{gathered} \pi(x) = R(x) - C(x)= 2.4x - (0.9x + 12\,000) = 1.5x - 12\,000.\end{gathered} \] Wir berechnen den Rentabilitätspunkt durch Gleichsetzen von Erlös und Kosten: \[ \begin{aligned} %% {alignat*}{2} R(x) = C(x)\quad\Rightarrow&\quad& 2.4x =&\; 0.9x + 12\,000\\[4pt] \quad\Rightarrow&\quad &x=&\; \frac{12\,000}{2.4-0.9}=8000\;\text{Flaschen pro Woche}.\end{aligned} \] Wenn der Break-even bei \(x=6000\) Flaschen pro Woche erreicht werden soll, dann erfordert das einen Verkaufspreis \(p\): \[ \begin{gathered} 6000=\frac{12\,000}{p-0.9}\implies p-0.9=2\implies p=2.9\,. \end{gathered} \] □
Musteraufgabe 1.9 Ein Unternehmen rechnet für die Produktion eines neuen Produktes mit Stückkosten von 45 GE. Die einmaligen Fixkosten für die Anschaffung der Produktionsmaschinen betragen 15000 GE. Pro Monat können 250 Stück des Produkts produziert werden. Wie soll der Preis pro Stück festgesetzt werden, wenn man nach vier Monaten einen Gewinn von 40000 GE erwirtschaftet haben will?
Lösung: Die Kostenfunktion lautet \(C(x)=45x+15000\), die Erlösfunktion ist \(R(x)=px\). Mit \(\pi(x)=R(x)-C(x)\) bezeichnen wir den erzielten Gewinn bei einem Absatz von \(x\) ME. Der angestrebte Gewinn soll nach 4 Monaten, also mit \(x=1000\) Stück erzielt werden. Das bedeutet \[ \begin{aligned} \pi(1000)=40000&=R(1000)-C(1000)\\ &=1000p-(45\cdot 1000+15000)\\ &=1000p - 60000.\end{aligned} \] Daraus ergibt sich \(p=100\). □
Musteraufgabe 1.10 Ein Unternehmen plant die Einführung eines neuen Produktes, für das 60 000 GE als Fixkosten veranschlagt sind. Die Produktion eines Stücks verursacht Kosten von 150 GE. Bei 1200 Stück soll der Break-even-Point erreicht werden. Aufgrund eines Patentstreits muss die Produktion nach Erzeugung von 300 Stück abgebrochen werden. Welcher Schaden ist dem Unternehmen dadurch entstanden?
Lösung: Die Kostenfunktion lautet \(C(x)=150x+60\,000\). Damit die Menge \(x=1200\) dem Break-even-Point entspricht, muss für diese Menge \(C(x)=R(x)\) gelten, dh. \[ \begin{gathered} 150\cdot 1200+60\,000=px=p\cdot 1200\implies 1200p=240000.\end{gathered} \] Daraus ergibt sich der notwendige Preis als \(p=200\). Wenn nun bei \(x=300\) der Verkauf gestoppt wird, dann entsteht als Schaden \[ \begin{gathered} C(300)-R(300)=150\cdot 300+60\,000-200\cdot 300=45\,000. \end{gathered} \] □
Musteraufgabe 1.11 Ein Transportunternehmer kauft einen neuen LKW zu \(784\,000\) GE. Die jährlichen Fixkosten, wozu auch die Rückzahlungsraten für den Ankauf zählen, betragen \(25\)% der Anschaffungskosten. Wenn der LKW eingesetzt wird, fallen pro Betriebstag \(480\) GE Personalkosten und \(590\) GE Treibstoffkosten an. Es können täglich \(8\) Transporte mit dem LKW durchgeführt werden; pro Transport beträgt der Erlös \(440\) GE. Nach wie vielen Tagen im Laufe eines Betriebsjahres ist der Einsatz des LKWs kostendeckend?
Lösung: Zunächst formulieren wir die Kostenfunktion \(C(x)\), wobei \(C(x)\) die Kosten sind, die bei einem Einsatz von \(x\) Tagen anfallen: \[ \begin{gathered} C(x)=480x+590x+784000\cdot 0.25=1070x+196000.\end{gathered} \] Anschließend stellen wir die Erlösfunktion \(R(x)\) auf, wobei \(R(x)\) die Einnahmen sind, die bei einem Einsatz von \(x\) Tagen erzielt werden: \[ \begin{gathered} R(x)=8\cdot 440\cdot x=3520x\,.\end{gathered} \] Um den Rentabilitätspunkt zu berechnen, setzen wir Erlös und Kosten gleich: \[ \begin{gathered} C(x)=R(x)\quad\Rightarrow\quad 1070x+196000=3520x \quad \Rightarrow \quad x=80\;\text{Tage}.\end{gathered} \] □
1.2 Quadratische Funktionen
Neben den linearen Funktionen bilden die quadratischen Funktionen eine weitere einfache, aber sehr wichtige Klasse von reellen Funktionen.
1.2.1 Funktionsterme
Definition 1.12 Unter einer quadratischen Funktion versteht man eine reelle Funktion mit einem Funktionsterm der Form \[ \begin{gathered} f(x)=ax^2+bx+c.\end{gathered} \tag{1.4}\]
Offenbar sind lineare Funktionen Spezialfälle von quadratischen Funktionen, wenn nämlich \(a=0\) ist. Daher nehmen wir im Folgenden an, dass \(a\ne 0\). Während der Graph einer linearen Funktion eine Gerade ist, ist der Formenreichtum bei quadratischen Funktionen ungleich größer: ihr Graph ist eine Parabel (siehe Abbildung 1.4).

Ist \(a>0\), so ist die Parabel nach oben offen (man sagt auch, sie ist konvex), und die Funktion nimmt im Scheitel \(x=S\) ihr Minimum an. Falls \(a<0\), dann ist die Parabel nach unten offen (konkav), und der Scheitel ist das Maximum der Funktion. Die Lage des Scheitelpunkts kann leicht ermittelt werden durch die bekannte Scheitelpunktformel: \[ \begin{gathered} S=-\frac{b}{2a}.\end{gathered} \tag{1.5}\]
Musteraufgabe 1.13 Bestimme den Scheitel der quadratischen Funktion \(f(x)=2x^2-4x+7\).
Lösung: Es ist \(a=2\) und \(b=-4\). Daher lautet die \(x\)-Koordinate des Scheitels \(S=-b/2a=4/(2\cdot 2)=1\). Um die \(y\)-Koordinate auszurechnen, setzen wir einfach die \(x\)-Koordinate in den Funktionsterm ein: \[ \begin{gathered} f(1)=2-4+7=5 \end{gathered} \] Also ist \((1,5)\) der Scheitel von \(f(x)\). □
1.2.2 Lineares Marktmodell (Monopol)
Wir werden in diesem Abschnitt typische Anwendungen kennenlernen, bei der die Analyse einer quadratischen Funktion im Vordergrund steht. Es geht um die Erlös- und Gewinnoptimierung eines Monopolisten. Dabei legen wir eine lineare Kostenfunktion und eine lineare Nachfragefunktion zugrunde. Das Problem der Gewinnoptimierung führt dann auf eine quadratische Funktion.
Erlösoptimierung
Ein Monopolist ist ein Anbieter, der sein Produkt als einziger auf dem Markt anbietet. Er kann den Preis seines Produkts beliebig wählen. Er steuert damit die Nachfrage nach seinem Produkt.
Angenommen, die Nachfragefunktion des Marktes lautet \(D(p)=-ap+\alpha\). Wenn der Monopolist den Preis \(p\) festlegt, dann beträgt sein Erlös \[ \begin{gathered} R(p)=p\cdot D(p)=-ap^2 + \alpha p.\end{gathered} \] Der Erlös ist also eine quadratische Funktion des Preises, deren Scheitel ein Maximum ist. Um den Erlös zu maximieren, muss der Monopolist den Preis \(p\) so wählen, dass \(p\) genau dem Scheitel von \(R(p)\) entspricht.
Sehen wir uns ein Beispiel an.
Musteraufgabe 1.14 Der Betreiber eines Skilifts besitzt in einem wunderschönen Skigebiet ein lokales Monopol. Vor zwei Jahren hatte der Betreiber bei einem Preis von 45 GE pro Stück 750 Tageskarten pro Tag verkaufen können. Als er im vergangenen Jahr den Preis auf 40 GE pro Karte senkte, stieg der Absatz auf 800 Karten pro Tag. Bei welchem Kartenpreis erzielt er die höchsten Einkünfte pro Tag?
Lösung: Zur Bestimmung der Erlösfunktion \(R(p) = p\cdot D(p)\) benötigen wir zunächst die Nachfragefunktion \(D(p) = -ap+\alpha\). Sie verläuft durch die Punkte \(P=(45,750)\) und \(Q=(40,800)\). Wir berechnen die Parameter \(a\) und \(\alpha\) mittels (1.2) und (1.3): \[ \begin{gathered} \text{Anstieg }=-a=\frac{\Delta q}{\Delta p}=\frac{800-750}{40-45}=-10\implies a=10\\ \text{mit Punkt }P:\quad\alpha=D(p)+ap\implies \alpha=750+45\cdot 10=1200. \end{gathered} \] So erhalten wir \(D(p) = -10p+1200\). Dies liefert uns die Erlösfunktion: \[ \begin{gathered} R(p) = -10p^{2}+1200p \end{gathered} \] Der Scheitel dieser quadratischen Funktion liegt in \[ \begin{gathered} p_{\max} = -\dfrac{1200}{2\cdot (-10)} = 60.\end{gathered} \] Daher wird bei einem Preis von \(60\) GE pro Tageskarte wird der größte Erlös erzielt.
Wir beantworten noch einige weitere Fragen.
Wie groß ist dann die Nachfrage? \[ \begin{gathered} D(p_{\max}) = D(60) = -10\cdot 60 + 1200 = 600.\end{gathered} \] Es werden also bei diesem Preis \(600\) Karten nachgefragt.
Bei welchem Preis verschwindet die Nachfrage? \[ \begin{gathered} D(p) = 0 \quad\Rightarrow\quad -10p+1200 = 0 \quad\Rightarrow\quad p = 120.\end{gathered} \] Dieses \(p\) wird auch Prohibitivpreis genannt.
Abbildung 1.5 illustriert unsere Rechnung.

Musteraufgabe 1.15 Eine Tanzschule bietet Partnerkurse zum Preis von 5260 GE pro Person an. Eine Preiserhöhung um 460 GE führt zum Verlust eines Paares. Bei einem Preis von 10580 GE pro Person gibt es keinen Interessenten mehr. Bei welchem Preis erzielt die Tanzschule ihren höchsten Erlös?
Lösung: Es sei \(q\) die Anzahl der Personen, die am Kurs teilnehmen. Der Angabe entnehmen wir zwei Punkte, durch die die Nachfragefunktion verlaufen muss: \(P(10580,0)\) und \(Q(10120,2)\), denn würde der Prohibitivpreis von 10580 um 460 reduziert, hätten wir ein Paar, d.h. zwei Teilnehmer mehr. Mittels (1.2) und (1.3), wobei \(k=-a\) und \(d=\alpha\): \[ \begin{gathered} k=-a=\frac{2-0}{10120-10580}=-\frac{1}{230}\implies a=\frac{1}{230},\\[5pt] d=\alpha=0-\left(-\frac{1}{230}\right)\cdot 10580=46\implies \alpha =46.\end{gathered} \] Somit lautet die Nachfragefunktion: \[ \begin{gathered} D(p) = -\frac{p}{230}+46,\end{gathered} \] und die Erlösfunktion: \[ \begin{gathered} R(p) = -\frac{p^2}{230}+46p.\end{gathered} \] Sie hat den Scheitel in \[ \begin{gathered} p_{\max} = -\frac{46}{-2/230}=5290.\end{gathered} \] Mit anderen Worten: bei einem Preis von \(5\,290\) GE pro Person ist der Erlös am größten.
Wie viele Personen werden bei dieser Preissetzung am Tanzkurs teilnehmen? \[ \begin{gathered} D(p_{\max}) = D(5290) = -\dfrac{1}{230}\cdot 5290 + 46=23\text{ Personen}.\end{gathered} \] Es werden \(23/2\) Personen, also 11–12 Paare, den Tanzkurs besuchen. □
Gewinnoptimierung
In diesem Abschnitt lernen wir anhand konkreter Beispiele, wie für einfache Monopol- und Konkurrenzmärkte mit linearer oder quadratischer Kostenfunktion das Problem der Gewinnoptimierung mit elementaren Hilfsmitteln gelöst werden kann. Im Falle komplizierterer Kostenfunktionen sind wir allerdings auf Methoden der Differentialrechnung angewiesen, die wir erst in Kapitel 3 diskutieren werden.
Ein Beherbergungsbetrieb hat tägliche Fixkosten von 8000 GE. Die variablen Kosten pro Bett betragen 100 GE. Wenn \(q\) gleich der Anzahl der belegten Betten ist, dann lautet die Kostenfunktion \[ \begin{gathered} C(q)=100q+8000.\end{gathered} \] Der Betrieb habe lokal eine Monopolstellung und kann daher durch den Übernachtungspreis die Nachfrage beeinflussen. Man weiß aus Erfahrung, dass beim Preis von 300 GE 40 Betten belegt werden. Eine Preissenkung um 20 GE würde die Belegzahl um ein Bett erhöhen. Zur Analyse der Gewinnsituation wird ein lineares Marktmodell zugrunde gelegt, indem man unterstellt, dass sich Preisveränderungen bei jedem Ausgangspreis ungefähr gleich auswirken.
Es sei \(p\) der Übernachtungspreis für ein Bett und \(D(p)=-ap+\alpha\) die Nachfragefunktion. Auf die übliche Weise ermitteln wir: \[ \begin{gathered} D(p)=-0.05p+55.\end{gathered} \] Der Gewinn \(\pi(p)\) ist die Differenz zwischen Erlösen und Kosten: \[ \begin{gathered} \pi(p)=R(p)-C(p).\end{gathered} \] Beachten Sie, dass hier die Kosten als Funktion des Preises auftreten, d.h. wir müssen in der Kostenfunktion \(C(q)\) die Variable \(q\) ausdrücken durch die eben ermittelte Nachfragefunktion \(q=D(p)\): \[ \begin{aligned} C(p)&=100q+8000=100(-0.05p+55)+8000\\ &=-5p+13500.\end{aligned} \] Die Erlöse ergeben sich wie immer aus dem Produkt Preis mal abgesetzter Menge: \[ \begin{gathered} R(p)=pD(p)=p(-0.05p+55)=-0.05p^2+55p.\end{gathered} \] Nun sind wir in der Lage, die Gewinnfunktion \(\pi(p)\) anzugeben: \[ \begin{aligned} \pi(p)&=R(p)-C(p)\\ &=-0.05p^2+55p-(-5p+13500)\\ &=-0.05p^2+60p-13500.\end{aligned} \] Dies ist eine quadratische Funktion, deren Maximum im Scheitel liegt. So können wir berechnen, wie das Unternehmen den Preis festsetzen muss, um maximalen Gewinn zu erzielen. Mit der Scheitelpunktformel finden wir: \[ \begin{gathered} p_{\text{opt}}=-\frac{60}{2(-0.05)}=600.\end{gathered} \] Dieser optimale Übernachtungspreis unterscheidet sich freilich von jenem Preis, der maximalen Erlös garantiert. Letzterer ergibt sich aus \(R(p)\): \[ \begin{gathered} p_{\text{max(R)}}=-\frac{55}{2(-0.05)}=550.\end{gathered} \] Siehe Abbildung 1.6 zur Illustration.

Musteraufgabe 1.17 Ein Fabrikant kann von einer Ware bei einem Preis von 120 GE 816 Stück, bei einem Preis von 240 GE aber nur 612 Stück absetzen. Dem Fabrikanten entstehen Fixkosten von 79600 GE und zusätzlich pro Stück Kosten von 60 GE. Berechnen Sie den Preis, bei dem der Fabrikant seinen größten Gewinn erzielt.
Lösung: Die Nachfragefunktion verläuft durch die Punkte \(P(120,816)\) und \(Q(240,612)\). Mit Hilfe von (1.2) und (1.3), errechnen wir: \[ \begin{gathered} D(p) = -1.7p+1020.\end{gathered} \] Die Erlösfunktion ist daher: \[ \begin{gathered} R(p) = pD(p)=-1.7p^2+1020p.\end{gathered} \] Es sei \(q\) die abgesetzte Menge. Der Angabe entnehmen wir die Kostenfunktion: \[ \begin{gathered} C(q)=60q+79600.\end{gathered} \] In der Kostenfunktion \(C(q)\) setzen wir erneut \(q=D(p)\): \[ \begin{gathered} C(p)=60(-1.7p+1020)+79600=-102p+140800.\end{gathered} \] Das ergibt schließlich die Gewinnfunktion: \[ \begin{aligned} \pi(p)&=R(p)-C(p)\\ &=-1.7p^2+1020p-(-102p+140800)\\ &=-1.7p^2+1122p-140800.\end{aligned} \] Sie besitzt ihr Maximum in: \[ \begin{gathered} p_{\text{opt}}=-\frac{1122}{2(-1.7)}=330.\end{gathered} \] In den folgenden Aufgaben behandeln wir die Situation eines Konkurrenzmarktes (Polypol), in dem Anbieter eine quadratische Kostenfunktion haben.
Musteraufgabe 1.18 Ein Unternehmen produziert ein Gut, das es zu einem Preis von 76 GE absetzen kann. Die Fixkosten der Produktion betragen 51700 GE, die variablen Kosten sind in Abhängigkeit von der produzierten Menge \(q\) \[ \begin{gathered} C_v(q)=\frac{1}{404} q^2+46q\;.\end{gathered} \] Bei welcher Produktionsmenge erzielt das Unternehmen den größten Gewinn?
Lösung: Der Gewinn als Funktion der abgesetzten Menge lautet: \[ \begin{aligned} \pi(q)&=R(q)-C(q)\\ &=76q-\left[\frac{1}{404} q^2+46q+51700\right]\\ &=-\frac{q^2}{404}+30q-51700.\end{aligned} \] Der Gewinn wird maximal bei \[ \begin{gathered} q_{\text{opt}}=-\frac{30}{2(-1/404)}=6060.\end{gathered} \] □
Musteraufgabe 1.19 Ein Unternehmen produziert ein Gut, dessen Preis durch staatliche Verordnung auf 120 GE festgesetzt wurde. Die Fixkosten der Produktion betragen 60000 GE, die variablen Kosten sind in Abhängigkeit von der produzierten Menge \(q\) \[ \begin{gathered} C_v(q)= 0.0019q^2+59q.\end{gathered} \] Das Unternehmen muss eine spezifische Mengensteuer von 20 GE pro abgesetzter Mengeneinheit abführen. Wie hoch ist der Gewinn, den das Unternehmen maximal erzielen kann?
Eine (auch nur teilweise) Überwälzung der Steuer auf die Konsumenten ist nicht möglich.
Lösung: Es sei \(t\) der Betrag in GE/ME, der als Mengensteuer1 beim Unternehmen eingehoben wird. Der Gewinn wird um die abzuführende Mengensteuer gemindert, also um den Betrag \(t\cdot q\). So lautet die Gewinnfunktion nun \[ \begin{aligned} \pi(q)&= R(q)-C(q)-t\cdot q\\ &=120q-[0.0019q^2+59q +60000]-t\cdot q\\ &=-0.0019q^2+(61-t)q-60000.\end{aligned} \] Die Scheitelpunktformel liefert die gewinnmaximierende Absatzmenge in Abhängigkeit von dem Steuersatz \(t\): \[ \begin{gathered} q^\ast(t) = \frac{-(61-t)}{2(-0.0019)}=\frac{61-t}{0.0038}.\end{gathered} \] Bei einem Steuersatz von \(t=20\) GE ergibt das: \[ \begin{gathered} q^\ast(20)=\frac{41}{0.0038}\simeq 10789.4737\text{ ME} \end{gathered} \] Durch Einsetzen in die Gewinnfunktion \(\pi(q)\) erhalten wird den Gewinn, den das Unternehmen maximal erzielen kann: \[ \begin{aligned} \pi(q^\ast(20)) &=-0.0019\cdot 10789.4737^2+41\cdot 10789.4737-60000\\ &=161184.2105\,. \end{aligned} \] Wenn der Staat diese Mengensteuer nicht einhebt, dann sind Angebot und Gewinn wesentlich höher. Durch eine einfache Kontrollrechnung können wir uns davon überzeugen, dass ohne Mengensteuer \((t=0)\): \[ \begin{gathered} q^\ast(0)=\frac{61}{0.0038}\simeq 16052.6316\quad\text{und}\quad \pi(q^\ast(0))=429605.2632\,.\end{gathered} \] Die Mengensteuer führt also nicht nur zu einer deutlichen Reduktion der abgesetzten und damit ebenso der produzierten Menge, es ergibt sich auch ein massiver Rückgang des Unternehmensgewinns. □
Bemerkung 1.20 (Überwälzung der Steuer) In diesem Beispiel wurde ausdrücklich angenommen, dass aufgrund gesetzlicher Maßnahmen die Unternehmen die Steuer nicht einmal teilweise auf die Nachfrager überwälzen können. Wenn diese Maßnahmen nicht getroffen werden, bewirkt die Steuer eine Änderung der Lage der Angebotsfunktion der Unternehmen. Bei gleichem Preis wird weniger angeboten. Dies bewirkt, dass auch die Konsumenten einen Teil der Steuerlast tragen müssen. Dieses Problem wird ausführlich in der Theorie des partiellen Marktgleichgewichts der Mikroökonomie behandelt.
Musteraufgabe 1.21 Ein Unternehmen der chemischen Industrie besitzt aufgrund eines Patents ein Monopol auf Pflanzenschutzmittel. Die Nachfragefunktion nach diesem Produkt im Großhandel lautet \[D(p): \;q= -1.4924p+2443\] Die Fixkosten betragen \(603015\) GE, die variablen Kosten sind gegeben durch \[C_v(q)= 0.6518q^2-667q\] Im Rahmen der Agrarförderung beschließt die Regierung, das Herbizid mit einem Betrag von 632 GE pro Tonne zu subventionieren um ein ausreichendes Angebot sicherzustellen. Um wieviele Tonnen nimmt durch diese Maßnahme die am Markt angebotene Menge zu?
Lösung: Wir drücken zuerst in der Nachfragefunktion den Preis als Funktion der Angebotsmenge \(q\) aus dadurch, dass wir \(p\) als Funktion von \(q\) ausrechnen: \[ \begin{gathered} D(p): \quad q= -1.4924p+2443\quad\implies\quad p= -0.6701q+1637\,. \qquad \mbox{(A)}\end{gathered} \] Das ist vorteilhaft, weil die Kosten ebenfalls als Funktion der Menge \(q\) gegeben sind. Wir bezeichnen nun mit \(s\) die Höhe der Subvention. Die Gewinnfunktion lautet somit: \[ \begin{aligned} \pi(q)&=\text{Erlös}-\text{Kosten}+ \text{Subvention}\\ &=( -0.6701q+1637)\cdot q- (0.6518q^2-667 q +603015) +s\cdot q\\ &=-1.3219q^2 +(2304+s) q-603015.\end{aligned} \] Daraus ergibt sich das gewinnmaximierende \(q^\ast\) als Funktion von \(s\): \[ \begin{gathered} q^\ast(s)=\frac{2304+s}{2.6438}.\end{gathered} \] Werden keine Subventionen gewährt, der Fall \(s=0\), dann beträgt das Angebot \[ \begin{gathered} q^\ast(0)=\frac{2304}{2.6438}=871.47.\end{gathered} \] Bei einer Subvention von 632 GE pro Tonne hingegen: \[ \begin{gathered} q^\ast(632)=\frac{2304+632}{2.6438}=1110.52\,.\end{gathered} \] Durch die Subvention erhöht sich also das Marktangebot um \[ \begin{gathered} \Delta q=q^\ast(632)-q^\ast(0)=1110.52-871.47=239.05\:\text{ME}.\end{gathered} \] Wie stellt sich der Preis für die Konsumenten dar? Es wäre naïv gedacht, der Preis würde sich um den Betrag der Subvention \(s=632\) pro Tonne reduzieren. Wir haben es immerhin mit einem Monopolmarkt zu tun! Wir setzen diese Mengen in die Nachfragefunktion (A) ein. Ohne Subvention beträgt die Nachfrage \(q=871.47\) Tonnen. Bei dieser Nachfrage beträgt der Preis pro Tonne: \[ \begin{gathered} s=0: \qquad p = -0.6701\cdot 871.47+1637= 1053.03 \,.\end{gathered} \] Wenn subventioniert wird, beläuft sich die Nachfrage auf \(q=1110.52\) Tonnen. Bei dieser Menge verlangt der Monopolist einen Preis von: \[ \begin{gathered} s=632: \qquad p = -0.6701\cdot 1110.52+1637= 892.84\,.\end{gathered} \] Der Preis pro Tonne ist also lediglich um 160.19 GE niedriger, die Differenz auf 632 GE (immerhin ca. 472 GE) kommt dem Monopolanbieter zugute. □
1.3 Arithmetische Folgen
1.3.1 Folgen
Folgen sind Funktionen, die natürlichen Zahlen \(n\) reelle Zahlen \(x_n\) zuordnen. Wir nennen \(n\) den Index der Folge und \(x_n\) das \(n\)-te Glied der Folge. Die einfachste denkbare Folge ist eine konstante Folge. Eine solche Folge hat die Form \(x_n=c\) für alle \(n=0,1,2,\ldots\).
Interessanter als konstante Folgen sind Zahlenfolgen, deren Werte sich zwar ändern, wobei aber die Veränderung selbst konstant ist. Die Folgenglieder solcher Folgen verändern sich vom Index \(n\) zum Index \(n+1\) immer in der gleichen Weise. Wenn man die Veränderung der Folgenglieder durch die Differenzen misst und diese konstant ist, dann entstehen so die arithmetischen Folgen.
Definition 1.22 Eine Zahlenfolge \(x_n\) ist eine arithmetische Folge, wenn die Differenzen \(\Delta x_n=x_n-x_{n-1}\) zwischen aufeinander folgenden Gliedern konstant sind.
Hier einige Beispiele:
Die Folge mit dem allgemeinen Glied \(x_n=n\) ist eine arithmetische Folge, weil die Differenz \(\Delta x_n=x_n-x_{n-1}=n-(n-1)=1\) konstant ist.
Die Folge mit dem allgemeinen Glied \(x_n=2n+1\) ist eine arithmetische Folge, weil die Differenz \(\Delta x_n=x_n-x_{n-1}=2n+1-(2(n-1)+1)=2\) konstant ist.
Die Folge mit dem allgemeinen Glied \(x_n=7-3n\) ist eine arithmetische Folge, weil die Differenz \(\Delta x_n=x_n-x_{n-1}=7-3n-(7-3(n-1))=-3\) konstant ist.
Die Folge mit dem allgemeinen Glied \(x_n=n^2\) ist keine arithmetische Folge, weil die Differenz \(\Delta x_n=x_n-x_{n-1}=n^2-(n-1)^2=2n-1\) von \(n\) abhängig, also nicht konstant ist.
Folgenterme
Man kann am Term des allgemeinen Folgengliedes \(x_n\) erkennen, ob es sich um eine arithmetische Folge handelt.
Satz 1.23 Eine Folge mit dem allgemeinen Glied \(x_n\) ist genau dann eine arithmetische Folge, wenn das allgemeine Glied die Form \[ \begin{gathered} x_n=x_0+nd\end{gathered} \tag{1.6}\] hat, dh. wenn der Term des allgemeinen Gliedes der Term einer linearen Funktion (von \(n\)) ist.
Begründung: Es sei \(x_n\) eine beliebige arithmetische Folge mit dem Anfangsglied \(x_0\) und der konstanten Differenz \(\Delta x_n=d\). Dann erhält man die Glieder der Folge durch \[ \begin{gathered} \begin{array}{lclcl} x_1&=&&&x_0+d\\ x_2&=&x_1+d&=&x_0+2d\\ x_3&=&x_2+d&=&x_0+3d\\ &&\ldots&&\\ x_n&=&&=&x_0+nd \end{array}\end{gathered} \] Also ist das allgemeine Folgenglied \(x_n=x_0+nd\) durch einen linearen Funktionsterm zu berechnen.
Manchmal ist es naheliegender, die Folge mit \(x_1\) beginnen zu lassen. In diesem Fall ändert sich das Bildungsgesetz (1.6) geringfügig. Weil \(x_1=x_0+d\) und damit \(x_0=x_1-d\), wird (1.6) zu \[ \begin{gathered} x_n=x_1+(n-1)d.\end{gathered} \tag{1.7}\] Damit haben wir verstanden, warum jede arithmetische Folge einen linearen Funktionsterm für das allgemeine Folgenglied besitzt. Ist aber auch umgekehrt jede Folge mit einem linearen Term eine arithmetische Folge?
Es sei \(x_n=bn+c\) eine beliebige Folge mit einem linearen Funktionsterm. Wir wollen uns davon überzeugen, dass diese Folge tatsächlich eine arithmetische Folge ist. Zu diesem Zweck bilden wir die Differenzen und erhalten \[ \begin{gathered} x_n-x_{n-1}=bn+c-(b(n-1)+c)=b.\end{gathered} \] Die Differenzen sind tatsächlich konstant (von \(n\) unabhängig) und deshalb ist \(x_n\) eine arithmetische Folge. □
Graphische Darstellung
Es gibt also, wie wir gesehen haben, einen engen Zusammenhang zwischen arithmetischen Folgen und linearen Funktionen. Dieser Zusammenhang wird besonders deutlich, wenn man den Graphen einer arithmetischen Folge zeichnet. Ist \(x_n=x_0+nd\) eine arithmetische Folge, dann liegen nämlich alle Punkte \((n,x_n)\) auf dem Graphen der linearen Funktion \(f(t)= x_0+td\). Die Abbildung 1.7 illustriert diesen Sachverhalt.

Der qualitative Verlauf des Graphen einer arithmetischen Folge hängt vom Vorzeichen der Differenz \(d\) ab. Wir fassen die ziemlich offensichtlichen Tatsachen in einem Satz zusammen.
Satz 1.24 Es sei \(x_n=x_0+nd\) eine arithmetische Folge.
(1) Ist \(d>0\), dann ist die Folge \((x_n)\) streng monoton wachsend, dh. \(x_n>x_{n-1}\) für alle \(n=1,2,\ldots\).
(2) Ist \(d<0\), dann ist die Folge \((x_n)\) streng monoton fallend, dh. \(x_n<x_{n-1}\) für alle \(n=1,2,\ldots\).
(3) Ist \(d=0\), dann ist die Folge \((x_n)\) konstant, dh. \(x_n=x_0\) für alle \(n=1,2,\ldots\).
Anwendungen
Wir sehen uns nun eine einfache Anwendung von arithmetischen Folgen an.
Ein Unternehmen will im dritten Jahr 7500 Stück eines Produktes herstellen und nach 10 Jahren das Produktionsniveau von 25 000 Stück erreichen. Die Produktionssteigerungen sollen jährlich konstant sein. Mit welcher Stückzahl muss im ersten Jahr begonnen werden und wieviel muss die jährliche Steigerung ausmachen?
Man kann diese Aufgabe sicherlich ohne jeden Bezug auf arithmetische Folgen ausschließlich mit dem Hausverstand lösen. Es ist aber nützlich, bereits bei einer so einfachen Aufgabe die mathematische Struktur des Problems deutlich zu machen.
Wir bezeichnen die Produktionszahlen der einzelnen Jahre mit \(x_1,x_2,\ldots, x_{10}\). Wenn die Produktionssteigerungen jährlich konstant sein sollen, bedeutet das, dass die Differenzen dieser Folge konstant sind. Daher handelt es sich um eine arithmetische Folge. Die Folgenglieder \(x_3=7500\) und \(x_{10}=25\,000\) sind vorgeschrieben. Wir sollen das Glied \(x_1\) und die Differenz \(\Delta x_n=d\) berechnen.
Da nun \(x_{10}-x_3=25000-7500=17500\) und überdies \[ \begin{gathered} x_{10}-x_{3}=(x_0+10d)-(x_0+3d)=7d,\end{gathered} \] folgt \(17\,500=7d\) und daher \(d=2500\). Die jährliche Produktionssteigerung muss also \(2500\) Stück ausmachen. Um das allgemeine Folgenglied auszurechnen, berechnen wir die Größe \(x_1\) aus \[ \begin{gathered} x_3=x_0+3d=x_1+2d \quad \Rightarrow \quad x_1=x_3-2d=2500.\end{gathered} \] Daher lautet unsere Folge \[ \begin{gathered} x_n=x_0+nd=x_1+(n-1)d=2500+2500(n-1)=2500n,\end{gathered} \] und der Startwert der Produktion im Jahr \(n=1\) ist \(x_1=2500\).
1.3.2 Summierung von Folgen
Summenformel
Wir geben nun eine Formel an, mit der man die Summe einer arithmetischen Folge direkt berechnen kann.
Satz 1.26 Die Summe der ersten \(n\) Glieder einer arithmetischen Folge \(x_1,x_2,\ldots,x_n\) beträgt \[ \begin{gathered} S_n=x_1+x_2+\cdots+x_n=n\cdot\dfrac{x_1+x_n}{2}.\end{gathered} \tag{1.8}\] Das ist der \(n\)-fache Mittelwert aus dem ersten und dem letzten Folgenglied.
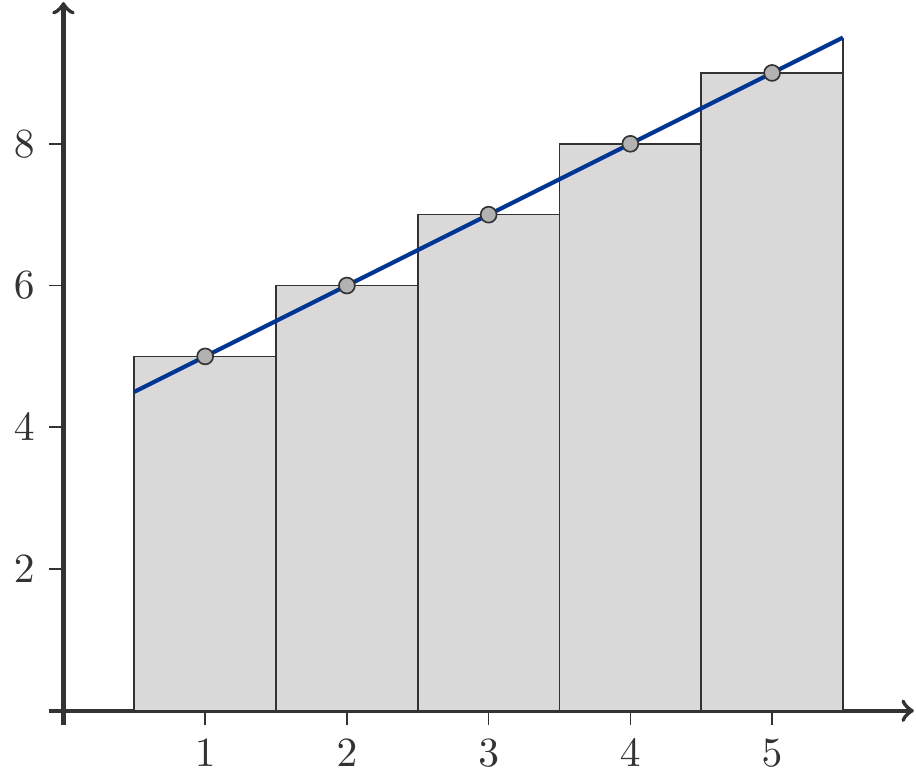
Bemerkung 1.27 In der Abbildung 1.8 sind die ersten fünf Glieder der arithmetischen Folge \[ \begin{gathered} x_1=5,\;x_2=6,\,x_3=7,\;x_4=8,\;x_5=9\end{gathered} \] durch fünf Balken veranschaulicht, deren Grundlinie gleich Eins ist und deren Höhe mit dem jeweiligen Folgenglied übereinstimmt.
Die Summe der fünf Folgenglieder ist daher identisch mit der Summe der Flächeninhalte der fünf Balken. Dieser gesamte Flächeninhalt ist aber zugleich identisch mit dem Flächeninhalt unter jener Geraden, die die fünf Folgenglieder verbindet. Wenn wir diesen Flächeninhalt geometrisch berechnen, erhalten wir genau die Formel (1.8): Länge der Grundlinie \(\times\) durchschnittliche Höhe: \[ \begin{gathered} \frac{x_1+x_5}{2}\cdot 5=\frac{5+9}{2}\cdot 5=35.\end{gathered} \]
Nun zum Beweis der Summenformel (1.8). Der Beweistrick ist Teil der abendländischen Kulturgeschichte und gehört daher zur Allgemeinbildung.
Wir schreiben die Summe zweimal, in jeweils umgekehrter Reihenfolge, an und addieren übereinander stehende Folgenglieder: \[ \begin{gathered} \begin{array}{l@{\;=\;}l@{\;+\;}l@{\;+\cdots+\;}l} S_n & x_1 &x_2 &x_n\\ S_n &x_n&x_{n-1}&x_1\\ \hline 2S_n & (x_1+x_n) & (x_2+x_{n-1}) & (x_n+x_1) \end{array}\end{gathered} \tag{1.9}\] Jetzt kommt die Pointe der Überlegung: Die Summen \(x_1+x_n\), \(x_2+x_{n-1}\), …, \(x_n+x_1\) sind alle gleich groß! In der Tat, weil \(x_2=x_1+d\) und \(x_n=x_{n-1}+d\), folgt beispielsweise, dass \[ \begin{gathered} x_2+x_{n-1}=(x_1+d)+x_{n-1}=x_1+(d+x_{n-1})=x_1+x_n. \end{gathered} \] Ähnlich zeigt man, dass alle übrigen Glieder der dritten Zeile von (1.9) auch gleich \(x_1+x_n\) sind. Dadurch wird die dritte Zeile von (1.9) zu \[ \begin{gathered} 2S_n=n(x_1+x_n),\end{gathered} \] was bereits mit unserer behaupteten Formel äquivalent ist. □
Bemerkung 1.28 Es gibt noch andere Möglichkeiten, die Summe von \(n\) aufeinander folgenden Gliedern einer arithmetischen Folge aufzuschreiben. Wenn eine arithmetische Folge mit \(x_1\) beginnt, dann ist \(x_n=x_1+(n-1)d\). Also gilt \[ \begin{gathered} S_n=n\cdot\dfrac{x_1+x_n}{2}=\dfrac{n}{2}(2x_1+(n-1)d).\end{gathered} \]
Anwendungen
Wo treten bei wirtschaftlichen Anwendungen Summen von arithmetischen Folgen auf? Wir beginnen zunächst mit einem einfachen Anwendungsbeispiel.
Musteraufgabe 1.29 Eine Bibliothek verleiht kostenlos Bücher an Studenten, die maximale Entlehnzeit beträgt 14 Tage. Wird diese Zeit überschritten, dann verrechnet die Bibliothek eine Strafgebühr von 6 GE pro Buch für den ersten Tag, und diese tägliche Strafgebühr erhöht sich von Tag zu Tag um weitere 2 GE. Wie hoch fällt die Strafe aus, wenn ein Buch um 8 Tage zu spät zurückgegeben wird?
Lösung: Die täglichen Strafgebühren bilden eine arithmetische Folge mit dem Anfangswert \(x_1=6\) und der Differenz \(d=2\), also \(x_n=6+2(n-1)\). Die für 8 Tage fällige Strafgebühr beträgt daher: \[ \begin{gathered} S_8=\frac{8}{2}\left(x_1+x_8\right)=4(6+6+2\cdot 7)=104.\end{gathered} \] □
Musteraufgabe 1.30 Die Baulandreserve einer Kleinstadt beträgt gegenwärtig 343000 \(m^2\). Während im laufenden Jahr exakt 12000 \(m^2\) verbaut werden, nimmt durch Zuzug und andere Faktoren die neu verbaute Fläche Jahr für Jahr um 2400 \(m^2\) zu. Nach wievielen Jahren verfügt die Stadt über keine Baulandreserve mehr?
Lösung: Die im ersten Jahr verbaute Fläche beträgt \(x_1=12000 \;m^2\), die im \(n\)-ten Jahr verbaute Fläche ist \(x_n=12000+2400(n-1)\; m^2\). Somit beträgt der Verbrauch an Bauland im Laufe von \(n\) Jahren: \[ \begin{gathered} \begin{array}{c@{\;=\;}l} S_n&x_1+x_2+\cdots+x_n=n\dfrac{24000+2400(n-1)}{2}\\[10pt] &12000n+1200n^2-1200n=1200n^2+10800n\,. \end{array}\end{gathered} \] Die Baulandreserve ist verbraucht, wenn \(S_n\) den Wert 343000 erreicht. Es ist also die quadratische Gleichung zu lösen: \[ \begin{gathered} 1200n^2+10800n-343000=0\,.\end{gathered} \] Diese Gleichung lösen wir mit der Auflösungsformel für quadratische Gleichungen: \[ \begin{gathered} ax^2+bx+c=0\implies x_{1,2}=\frac{-b\pm\sqrt{b^2-4ac}}{2a}.\end{gathered} \] Damit finden wir die beiden Lösungen: \[ \begin{aligned} &n_{1,2}=\frac{-10800\pm\sqrt{10800^2-4\cdot 1200\cdot (-343000)}}{2 \cdot 1200} \\ &\implies\left\{\begin{array}{ccr} n_1 &=& 12.995\\ n_2&=&-21.995 \end{array}\right.\end{aligned} \] Nur die positive Lösung \(n_1=12.995\approx 13\) ist für uns interessant. Die Baulandreserve ist also nach ziemlich genau 13 Jahren verbraucht. □
Arithmetisch degressive Abschreibungen sind eine weitere Anwendung.
Musteraufgabe 1.31 Ein Wirtschaftsgut mit einem Anschaffungswert von 241 800 GE soll innerhalb von 12 Jahren arithmetisch degressiv abgeschrieben werden. Das heißt, die Abschreibungsbeträge bilden eine fallende arithmetische Folge \(x_1,x_2,\ldots,x_{12}\) mit \(x_{13}=0\). Wie sind die Abschreibungsbeträge zu wählen?
Lösung: Die vollständige Abschreibung innerhalb von 12 Jahren bedeutet, dass die Summe der Abschreibungsbeträge dem Anschaffungswert entsprechen soll. Bezeichnet man den letzten Abschreibungsbetrag mit \(d\), dann lautet die Folge der Abschreibungsbeträge \[ \begin{gathered} 12d,\,11d,\,10d,\ldots,\, 2d,\,d. \end{gathered} \] Also muss gelten: \[ \begin{aligned} 241\,800 &=12d+11d+10d+\cdots+2d+d\\[5pt] &=12\cdot\frac{12d+d}{2}=78d.\end{aligned} \] Daher ist \(d=3100\). Der erste Abschreibungsbetrag ist \(x_1=12d=37200\). Er sinkt jährlich um \(d=3100\), dh. \[ \begin{gathered} x_n=x_1-(n-1)d=37200-(n-1)3100,\end{gathered} \] bis er schließlich bei \(x_{12}=d=3100\) endet. □
Die folgende Aufgabe stammt aus einem der bekanntesten Werke Leonhard Eulers, Vollständige Anleitung zur Algebra. Dieses Buch, das weite Verbreitung fand, ist 1770 erschienen. Auf Seite 163 findet sich:
Musteraufgabe 1.32 Jemand kauft ein Pferd unter der Bedingung, dass er für den ersten Hufnagel 5 Groschen, für den zweiten 8, für den dritten 11, und immer 3 Groschen mehr für jeden folgenden zahlen soll. Es sind aber im Ganzen 32 Nägel. Wieviel muss er für das Pferd bezahlen?
Lösung: Es sei \(x_n\) der Beitrag des \(n\)-ten Hufnagels zum Kaufpreis. Die \(x_n\) bilden eine arithmetische Folge mit \(x_1=5\) und \(d=3\), sowie \(x_n=5+3(n-1)\). Der Kaufpreis selbst ergibt sich als Summe: \[ \begin{aligned} P&=x_1+x_2+\ldots+x_{32}=32\,\frac{x_1+x_{32}}{2}=16(5+5+31\cdot 3)\\[4pt] &= 1648 \text{ Groschen}.\end{aligned} \] Da zu Eulers Zeiten 30 Groschen einem Thaler entsprachen, betrug der Kaufpreis 54 Thaler und 28 Groschen. □
1.4 Weitere Übungsaufgaben
-
In einem Betrieb werden Rohre erzeugt. Die fixen Kosten für diese Produktion betragen 59400 GE, die variablen Kosten sind 157 GE pro Meter erzeugten Rohres. Beim Verkauf von einem Meter Rohr wird ein Erlös von 190 GE erzielt. Bei wieviel Metern Rohr wird der Break-even-Point erreicht?
Lösung: \(1800\)
-
Ein Hotel mit 930 Zimmern macht einen Gewinn von 210 GE pro Tag und belegtem Zimmer. Ein unbelegtes Zimmer verursacht einen Verlust von 100 GE pro Tag. Wieviele Zimmer müssen mindestens belegt sein, damit das Hotel ohne Verlust arbeiten kann?
Lösung: \(300\)
-
Die fixen Kosten für die Anschaffung der Betriebsmittel zur Erzeugung einer Ware betragen 259578 GE. An einem Tag werden 69 Stück produziert, die Herstellungskosten pro Stück betragen 33 GE. Ein Stück wird um 90 GE verkauft. Nach wievielen Produktionstagen erreicht das Unternehmen den Break-even-Point?
Lösung: \(66\)
-
Ein Unternehmen rechnet für die Produktion eines neuen Produkts mit Stückkosten von 52 GE. Die Fixkosten betragen 413480 GE. Pro Monat können 440 Stück hergestellt werden. Wie teuer soll die Ware verkauft werden, wenn man nach 11 Monaten einen Gewinn von 177000 GE erwirtschaftet haben will?
Lösung: \(174\)
-
Eine Firma bringt ein neues Produkt auf den Markt, dessen Produktionskosten pro Stück 70 GE betragen, die kalkulierten monatlichen Fixkosten belaufen sich auf 78000 GE. Die Marketingabteilung des Unternehmens setzt den Preis des Produkts so fest, dass der Break-even-Point bei einer Ausbringung von 2000 Stück erreicht würde. Wegen eines zu spät erkannten Konstruktionsfehlers muss allerdings die Produktion schon nach 500 Stück eingestellt werden. Wie hoch ist der Verlust, der dem Unternehmen dadurch entstanden ist?
Lösung: \(58500\)
-
Eine Arbeitsagentur hat 600 Handwerker unter Vertrag. Kann ein Handwerker als Leiharbeiter vermittelt werden, dann beträgt der Tagesgewinn, der mit diesem Handwerker erzielt wird, 460 GE. Ein Handwerker, der nicht beschäftigt wird, verursacht hingegen einen Verlust von 140 GE pro Tag. Wieviele der Handwerker müssen pro Tag mindestens als Leiharbeiter vermittelt werden, sodass die Agentur keine Verluste macht?
Lösung: \(140\)
-
Ein Monopolist setzt ein Gut ab, dessen Nachfrage in linearer Weise vom festgesetzten Preis abhängt. Der Monopolist erzielt maximalen Erlös bei einem Preis von 100 GE. Bei diesem Preis beträgt die Nachfrage 20 Stück. Wie groß wäre der Erlös bei einem Preis von 160 GE?
Lösung: \(1280\)
-
Ein Unternehmen produziert ein Gut, das es zu einem gesetzlich festgelegten Preis von 138 GE absetzen kann. Die Fixkosten der Produktion betragen 176000 GE, die variablen Kosten sind in Abhängigkeit von der produzierten Menge \(q\) \[ \begin{gathered} C_v(q)= 0.0053q^2+31q. \end{gathered} \] Das Unternehmen muss eine Wertsteuer von 19 % des Verkaufserlöses abführen. Wie hoch ist der maximal erzielbare Gewinn des Unternehmens, wenn aufgrund gesetzlicher Maßnahmen eine Überwälzung der Steuer auf die Konsumenten nicht möglich ist?
Hinweis: Bei einem Umsatz von \(p\cdot q\) und einem Steuersatz von \(t\) beträgt der vom Unternehmen abzuführende Steuerbetrag \(t\cdot p\cdot q\).
Lösung: \(131802.28\)
-
Ein Unternehmen kann sein Produkt zu einem Preis von 100 GE absetzen. Es produziert mit der Kostenfunktion (\(x\) Produktionsmenge): \[ C(x)=x^2+6x+1480. \] Bei welcher Absatzmenge \(x_0\) erreicht das Unternehmen die Gewinnzone?
Lösung: \(20\)
-
Ein Unternehmen produziert mit Kostenfunktion \(C(x)=24x+61200\). Zur Zeit verfügt es über eine monatliche Produktionskapazität von 3600 Einheiten. Welcher Marktpreis pro Einheit muss erzielbar sein, damit das Unternehmen seinen maximal erzielbaren Output kostendeckend absetzen kann?
Lösung: \(41\)
-
Ein Unternehmen betreibt im Stadtzentrum eine Tiefgarage mit Stellplätzen für PKWs ausschließlich für Dauerparker, die Mindestlaufzeit eines Vertrags beträgt 1 Monat. In der Garage ist Platz für maximal 88 PKWs. Eine Auslastung von 75% wird erzielt, wenn das Monatsentgelt pro PKW 600 GE beträgt. Würde das Monatsentgelt um 100 GE erhöht, führte das zum Verlust eines Kunden. Wieviel soll für einen Stellplatz pro Monat verlangt werden, sodass der Erlös des Garagenbetreibers maximal wird?
Lösung: \(3600\)
-
Ein Unternehmen produziert ein Gut, das es zu einem Preis von 90 GE absetzen kann. Die Fixkosten der Produktion betragen 48200 GE, die variablen Kosten sind in Abhängigkeit von der produzierten Menge \(q\) \[ \begin{gathered} C_v(q)=\frac{1}{338} q^2+58q\,. \end{gathered} \] Bei welcher Produktionsmenge erzielt das Unternehmen den größten Gewinn?
Lösung: \(5408\)
-
Ein Monopolanbieter besitzt Nachfragefunktion \(D(p)\) und Kostenfunktion \(C(q)\) gegeben durch \[ \begin{aligned} D(p): \;q &= -1.8665p+1230,\\ C(q) &= 0.4275q^2-168 q+79528 \end{aligned} \] Bei welcher Produktionsmenge \(q\) erzielt er maximalen Gewinn?
Lösung: gerundet \(429\)
-
Ein Investitionsgut im Wert von \(252\,000\) GE soll innerhalb von \(5\) Jahren arithmetisch degressiv abgeschrieben werden. Berechnen Sie den ersten und den letzten Abschreibungsbetrag.
Lösung: \(x_1=84000, x_5=16800\).
-
Jemand verpflichtet sich, 30 Jahre lang am Ende jeden Jahres einen Betrag zu zahlen, der Jahr für Jahr um einen konstanten Wert erhöht wird. Die Zahlung beträgt im 5. Jahr 3900 GE, im 20. Jahr 5400 GE. Wieviel ist insgesamt in den 30 Jahren zu bezahlen, ohne Berücksichtigung von Zinsen?
Lösung: \(148500\)
-
14500 Stück einer Ware sollen innerhalb von 29 Tagen verkauft werden. Am ersten Tag werden 150 Stück verkauft. Um wieviel Stück muss die verkaufte Stückzahl täglich gesteigert werden, damit nach 29 Tagen alle Waren verkauft sind?
Lösung: \(25\)
-
Im ersten Jahr beträgt die Ausbeute einer Edelmetallmine 2500 Tonnen pro Jahr, allerdings sinkt diese pro Jahr gleichmäßig um 125 Tonnen. Bei der aktuellen Kostenstruktur des Bergbauunternehmens liegt der Break-even-Point bei 1625 Tonnen. Wieviele Jahre kann die Mine noch wirtschaftlich betrieben werden?
Lösung: \(8\)
-
Die Finanzbehörden bewilligen der Firma X AG, die neu angeschaffte Schleudergussmaschine arithmetisch degressiv abzuschreiben. Berechnen Sie den 9. Abschreibungsbetrag, wenn die Anschaffungskosten der Maschine 376200 GE betragen und sie eine Nutzungsdauer von 11 Jahren hat.
Lösung: \(17100\)
-
In einem Paketverteilerzentrum sollen 9700 Pakete innerhalb von 25 Stunden den einzelnen Zustellern zugeteilt werden. In der ersten Stunde gelingt es, lediglich 40 Pakete zuzuteilen. Um wieviel Stück muss die Anzahl der zugeteilten Pakete pro Stunde gesteigert werden, sodass nach 25 Stunden alle Pakete zugeteilt sind?
Lösung: \(29\)
Die Mineralölsteuer ist ein prominentes Beispiel für eine Mengensteuer.↩︎