3  Differentialrechnung

3.1 Die Ableitung einer Funktion

3.1.1 Der Begriff der Ableitung

Bei unseren Untersuchungen über lineare Funktionen in Abschnitt 1.1 haben wir das Steigungsverhältnis einer Funktion auf einem Intervall kennengelernt. Der Name Steigungsverhältnis weist auf eine geometrische Eigenschaft hin, und wir kennen auch die geometrische Deutung dieser Eigenschaft am Funktionsgraphen. Wir kommen jetzt in Zusammenhang mit nichtlinearen Funktionen wieder auf das Steigungsverhältnis zurück.

Differenzenquotienten

Es sei \(f\) eine reelle Funktion und \([x_0,x]\) ein Intervall, das ganz im Definitionsbereich von \(f\) enthalten ist. Das Steigungsverhältnis der Funktion \(f\) auf dem Intervall berechnet man durch den Differenzenquotienten \[ \begin{gathered} \frac{f(x)-f(x_0)}{x-x_0} \end{gathered} \tag{3.1}\] der Funktion auf dem Intervall \([x_0,x]\). Dieser Differenzenquotient ist eine sehr wichtige Größe. An seine geometrische Deutung als Steigungsverhältnis auf dem Intervall \([x_0,x]\) haben wir schon erinnert. Will man den Differenzenquotienten ohne Bezug auf geometrische Vorstellungen deuten, dann interpretiert man ihn als durchschnittliche Änderung der Funktion auf dem Intervall \([x_0,x]\). Der Zähler der Formel (3.1) gibt die gesamte Änderung \(f(x)-f(x_0)\) der Funktion auf dem Intervall an, und wenn man die gesamte Änderung durch die Länge \(x-x_0\) des Intervalls teilt, erhält man die durchschnittliche Änderung.

Abbildung 3.1: Zum Differenzenquotienten.

Bei linearen Funktionen enthält der Differenzenquotient tatsächlich die gesamte Information, die man überhaupt erhalten kann, wenn man sich dafür interessiert, wie stark sich die Funktion ändert. Es spielt keine Rolle, welches Intervall man für die Berechnung des Differenzenquotienten verwendet. Für lineare Funktionen liefert jedes Intervall den gleichen Wert, weil das Steigungsverhältnis konstant ist.

Bei nichtlinearen Funktionen ist das aber anders. Je nachdem, welches Intervall man der Berechnung des Differenzenquotienten zugrundelegt, ergibt sich ein anderer Wert. Dies ist nicht überraschend, weil bei nichtlinearen Funktionen das Steigungsverhältnis variabel ist. Um einen vollständigen Überblick zu gewinnen, müssten wir daher für alle denkbaren Intervalle, auf denen die Funktion definiert ist, die Differenzenquotienten (die Steigungsverhältnisse) angeben. Dies ist aber sehr umständlich und wir sind deshalb daran interessiert, wie man sich auf einfachere Weise einen Überblick über die variablen Werte der Steigungsverhältnisse einer nichtlinearen Funktion verschaffen kann.

Das Problem wäre dann einfacher, wenn es gelingt, eine Größe zu definieren, deren inhaltliche Bedeutung so etwas wie das Steigungsverhältnis der Funktion in einem bestimmten Punkt darstellt. Dies ist nicht ganz einfach, denn einen Differenzenquotienten in einem Punkt \(x_0\), also \[ \begin{gathered} \frac{f(x_0)-f(x_0)}{x_0-x_0} \end{gathered} \tag{3.2}\] gibt es nicht. Der Quotient ist sinnlos, weil sowohl der Zähler als auch der Nenner gleich Null sind. Aber wenn wir uns auf den Standpunkt stellen, statt eines Punktes würde auch ein sehr kleines Intervall um den Punkt \(x_0\) das gleiche leisten, dann befinden wir uns auf der richtigen Fährte.

Der Grenzübergang

Wir betrachten eine Funktion \(y=f(x)\) und wollen das Steigungsverhältnis im Punkt \(x_0\) berechnen. Da es, wie schon erwähnt, nicht möglich ist, einen Differenzenquotienten an der Stelle \(x_0\) auszurechnen, untersuchen wir kleine Intervalle, die den Punkt \(x_0\) als einen Randpunkt besitzen. Es sei also \(x\) ein Punkt in der Nähe von \(x_0\), der aber von \(x_0\) verschieden ist. Wir wollen wissen, welche Werte der Differenzenquotient annimmt, wenn wir mit dem Punkt \(x\) immer näher an \(x_0\) heranrücken. Sehen wir uns ein Beispiel an.

Beispiel 3.1 (Steigungsverhältnis in einem Punkt)

Es sei \(f(x)=x^2\). Wir untersuchen die Differenzenquotienten für Intervalle, die \(x_0=2\) als einen Randpunkt besitzen. Der zweite Randpunkt der Intervalle sei \(x\). Wir wählen \(x\) sowohl rechts als auch links von \(x_0\) und rücken mit \(x\) immer näher an \(x_0\) heran. Dieses Heranrücken bewerkstelligen wir durch zwei Zahlenfolgen. Die erste Folge (linke Tabelle) hat das Bildungsgesetz \(x_n=2+1/(n+1)\), die zweite Folge (rechte Tabelle) \(x_n=2-1/(n+1)\), jeweils mit \(n=1,2,3,\ldots\). Beide Folgen streben gegen den Limes \(x_0=2\).

Die dabei entstehenden Werte des Differenzenquotienten \(\frac{f(x_n)-f(x_0)}{x_n-x_0}\) sind in den folgenden Tabellen enthalten.

\[ \begin{gathered} \begin{array}{rcc} \hline n& x_n & \text{Differenzenquotient}\\ \hline 1 & 2.500 &4.500 \\ 2 & 2.250 &4.250 \\ 3 & 2.125 &4.125 \\ 4 & 2.063 &4.063 \\ 5 & 2.031 &4.031 \\ 6 & 2.016 &4.016 \\ 7 & 2.008 &4.008 \\ 8 & 2.004 &4.004 \\ 9 & 2.002 &4.002 \\ 10 & 2.001 &4.001 \\ \hline \end{array}\qquad \begin{array}{rcc} \hline n & x_n & \text{Differenzenquotient}\\ \hline 1 & 1.500 &3.500 \\ 2 & 1.750 &3.750 \\ 3 & 1.875 &3.875 \\ 4 & 1.938 &3.938 \\ 5 & 1.969 &3.969 \\ 6 & 1.984 &3.984 \\ 7 & 1.992 &3.992 \\ 8 & 1.996 &3.996 \\ 9 & 1.998 &3.998 \\ 10 & 1.999 &3.999 \\ \hline \end{array} \end{gathered} \]

Wir sehen aus den Tabellen, dass sich die Werte des Differenzenquotienten offenbar an die Zahl 4 annähern; sie konvergieren gegen 4! Wir haben das dadurch erreicht, dass wir für die Randpunkte \(x\) der Intervalle den Beginn einer konvergenten Folge mit dem Limes \(x_0=2\) eingesetzt haben. Es liegt daher nahe, den Grenzwert der Differenzenquotienten als Wert für das Steigungsverhältnis der Funktion \(f(x)=x^2\) im Punkt \(x_0=2\) festzulegen.

Definition der Ableitung

Die folgende Definition legt nun fest, was wir unter dem Steigungsverhältnis einer Funktion an einem Punkt verstehen wollen. Die mathematische Bezeichnung für dieses Konzept ist die Ableitung.

Definition 3.2 Es sei \(f\) eine Funktion auf einem Intervall und \(x_0\) sei ein innerer Punkt des Intervalls.

Wenn für jede konvergente Folge \(x_n, n=1,2,\ldots\) und \(x_n\not=x_0\), mit dem Grenzwert \(x_0\) die Folge der Differenzenquotienten \[ \begin{gathered} \frac{f(x_n)-f(x_0)}{x_n-x_0} \end{gathered} \] konvergiert und zwar immer gegen den gleichen Grenzwert, dann nennen wir die Funktion \(f\) differenzierbar an der Stelle \(x_0\). Der Grenzwert selbst heißt Ableitung der Funktion \(f\) an der Stelle \(x_0\) und wird mit \(f'(x_0)\) bezeichnet.

Man verwendet häufig die Schreibweise \[ \begin{gathered} f'(x_0):= \lim_{x\to x_0} \frac{f(x)-f(x_0)}{x-x_0}. \end{gathered} \tag{3.3}\] Damit soll ausgedrückt werden, dass ein Grenzwert der Differenzenquotienten für jede Folge \(x_n\to x_0\) existiert, und dass dieser Grenzwert \(f'(x_0)\) genannt wird. Es sind noch andere Schreib- und Sprechweisen in Gebrauch. Den Vorgang der Berechnung einer Ableitung \(f'(x_0)\) nennt man das Differenzieren der Funktion. Man nennt die Ableitung \(f'(x_0)\) häufig den Differentialquotienten und bezeichnet sie dann durch \[ \begin{gathered} f'(x_0)=\frac{df}{dx}(x_0). \end{gathered} \] Damit soll die Verwandtschaft der Ableitung mit einem Differenzenquotienten angedeutet werden. Geht man von einer Funktionsgleichung \(y=f(x)\) aus, so ist es sogar üblich die Ableitung in der Form \[ \begin{gathered} f'(x_0)=\frac{dy}{dx}(x_0) \end{gathered} \] zu schreiben, obwohl damit die Funktion \(f\) in der Bezeichnung völlig verlorengeht. Man soll daher diese Bezeichnung nur dann verwenden, wenn dadurch keine Missverständnisse entstehen können.

Ableitung und Monotonie

Aus der Definition der Ableitung ergeben sich unmittelbar die folgenden Aussagen über das Vorzeichen der Ableitung:

• Ist die Funktion \(f\) auf dem Definitionsintervall monoton wachsend, dann ist die Ableitung \(f'(x_0)\ge 0\).

• Ist die Funktion \(f\) auf dem Definitionsintervall monoton fallend, dann ist die Ableitung \(f'(x_0)\le 0\).

Man kann noch Genaueres über die Beziehung zwischen der Monotonie der Funktion \(f\) und dem Vorzeichen der Ableitung sagen. Dies wird im Abschnitt 3.4.1 geschehen.

Erste Beispiele

Bevor wir uns ausführlich mit der anschaulichen Deutung der Ableitung auseinandersetzen, sehen wir uns einige konkrete Beispiele an. In diesen Beispielen berechnen wir Ableitungen durch einen Grenzübergang, wie er in der Definition der Ableitung beschrieben wird. Diese Art, Ableitungen zu berechnen, ist aber nicht die einfachste und auch nicht die übliche Vorgangsweise. Vielmehr kann man Ableitungen wesentlich schneller und einfacher mit den Regeln des sogenannten Differentialkalküls berechnen. Diese Regeln werden wir etwas später kennenlernen. Die Beispiele, die wir uns jetzt ansehen werden, dienen nur dem Zweck, die Definition der Ableitung besser zu verstehen.

Beispiel 3.3 (Ableitung einer linearen Funktion)

Es sei \(f(x)=ax+b\) eine lineare Funktion. Dann hat jeder Differenzenquotient den Wert \[ \begin{gathered} \frac{f(x)-f(x_0)}{x-x_0}=\frac{ax+b-ax_0-b}{x-x_0} =\frac{a(x-x_0)}{x-x_0}=a. \end{gathered} \] Das haben wir auch schon in Kapitel 1 gesehen. Beim Grenzübergang \(x\to x_0\) ist daher die Folge der Differenzenquotienten eine konstante Folge mit dem Limes \[ \begin{gathered} \lim_{x\to x_0} \frac{f(x)-f(x_0)}{x-x_0}=\lim_{x\to x_0}a=a. \end{gathered} \] Also beträgt die Ableitung einer linearen Funktion stets \(f'(x_0)=a\), gleichgültig in welchem Punkt \(x_0\) man die Ableitung bildet.

Beispiel 3.4 (Ableitung einer quadratischen Funktion)

Es sei \(f(x)=2x^2+3x+1\) eine quadratische Funktion. Wir berechnen die Ableitung an einem Punkt \(x_0\) durch einen Grenzübergang beim Differenzenquotienten.

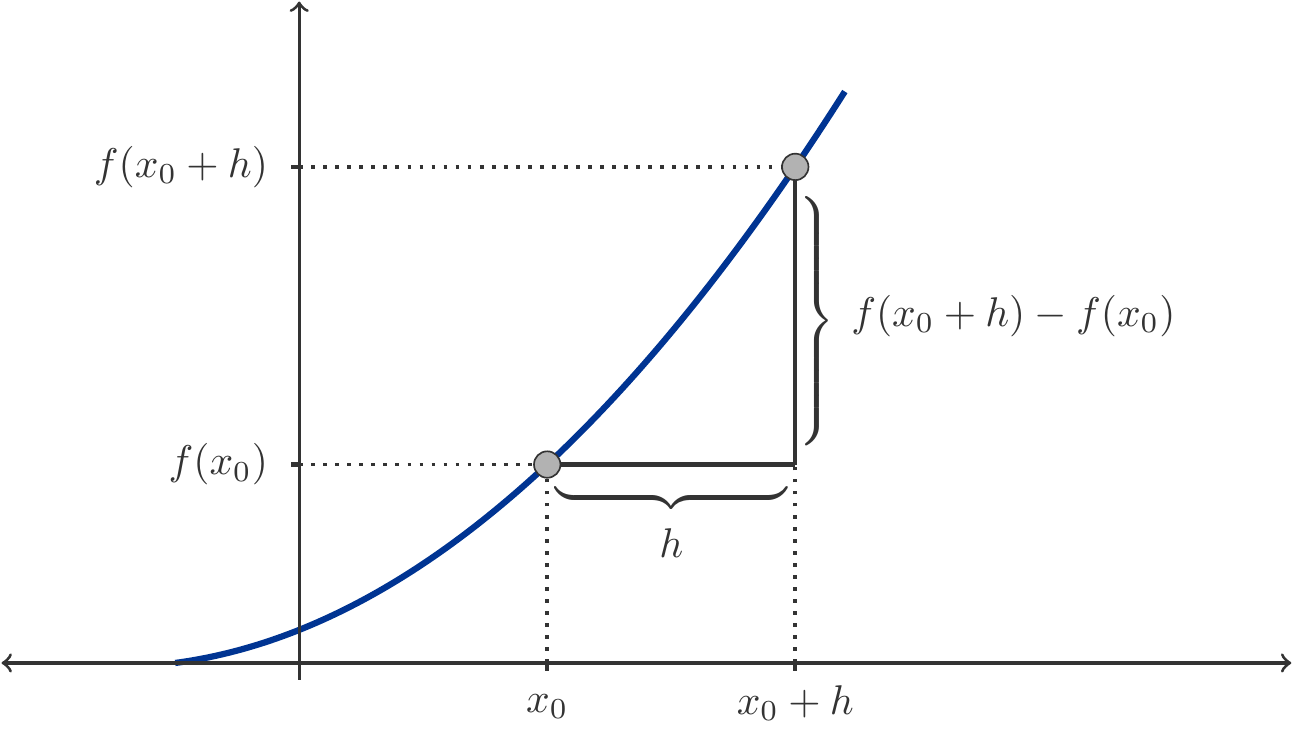
Es ist günstig und meistens wesentlich übersichtlicher, wenn man den Abstand zwischen den Randpunkten des Intervalls durch einen Buchstaben abkürzt, z.B. \(h:=x-x_0\). Dann ist \(x=x_0+h\) und der Grenzübergang \(x\to x_0\) ist äquivalent mit \(h\to 0\) (vgl. Abbildung 3.2).

Mit dieser Schreibweise lautet der Differenzenquotient \[ \begin{aligned} \frac{f(x)-f(x_0)}{x-x_0}&= \frac{f(x_0+h)-f(x_0)}{h}\\ &= \frac{2(x_0+h)^2+3(x_0+h)+1-2x_0^2-3x_0-1}{h}\\ &= \frac{4x_0h+2h^2+3h}{h}\\ &= 4x_0+2h+3. \end{aligned} \] Wir führen nun den Grenzübergang \(h\to 0\) und erhalten \[ \begin{aligned} f'(x_0) &=\lim_{h\to 0}\frac{f(x_0+h)-f(x_0)}{h} \\ &= \lim_{h\to 0} (4x_0+2h+3)=4x_0+3. \end{aligned} \] In diesem Beispiel hängt die Ableitung sehr wohl vom Punkt \(x_0\) ab. Für verschiedene Punkte \(x_0\) erhalten wir verschiedene Werte der Ableitung.

Abbildung 3.2: Differenzenquotient, \(f(x)=2x^2+3x+1\).

Beispiel 3.5 (Ableitung von \(f(x)=1/x\))

Es sei \(\displaystyle f(x)=\frac{1}{x}\). Der Differenzenquotient an einer Stelle \(x_0\not=0\) hat die Form \[ \begin{aligned} \frac{f(x_0+h)-f(x_0)}{h} &= \frac{\dfrac{1}{x_0+h}-\dfrac{1}{x_0}}{h} \\ &= \frac{x_0-(x_0+h)}{h(x_0+h)x_0} \\ &= -\frac{1}{(x_0+h)x_0}. \end{aligned} \tag{3.4}\] Durch den Grenzübergang \(h\to 0\) erhalten wir \[ \begin{aligned} f'(x_0) &= \lim_{h\to 0}\frac{f(x_0+h)-f(x_0)}{h} \\ &= -\lim_{h\to 0} \frac{1}{(x_0+h)x_0}=-\frac{1}{x_0^2}. \end{aligned} \tag{3.5}\]

Beispiel 3.6 (Ableitung von \(f(x)=\sqrt{x}\))

Es sei \(f(x)=\sqrt{x}\). Der Differenzenquotient an einer Stelle \(x_0>0\) lautet \[ \begin{gathered} \frac{f(x_0+h)-f(x_0)}{h}=\frac{\sqrt{x_0+h}-\sqrt{x_0}}{h}. \end{gathered} \] Um den Limes des Differenzenquotienten für \(h\to 0\) zu bestimmen, müssen wir eine trickreiche Umformung vornehmen. Wir erweitern den Bruch durch Multiplikation mit \(\sqrt{x_0+h}+\sqrt{x_0}\) in Nenner und Zähler und nutzen die bekannte Beziehung \((a-b)(a+b)=a^2-b^2\): \[ \begin{gathered} \dfrac{\sqrt{x_0+h}-\sqrt{x_0}}{h}= \dfrac{(\sqrt{x_0+h}-\sqrt{x_0})(\sqrt{x_0+h}+\sqrt{x_0})}{h(\sqrt{x_0+h}+\sqrt{x_0})}\\ =\dfrac{x_0+h-x_0}{h(\sqrt{x_0+h}+\sqrt{x_0})}=\dfrac{1}{\sqrt{x_0+h}+\sqrt{x_0}}. \end{gathered} \] Nun können wir den Grenzübergang \(h\to 0\) durchführen und erhalten \[ \begin{gathered} f'(x_0)=\dfrac{1}{2\sqrt{x_0}}. \end{gathered} \tag{3.6}\]

3.1.2 Die geometrische Deutung der Ableitung

Wir wenden uns nun der Deutung des Begriffs der Ableitung zu. Historisch ist der Begriff der Ableitung gleichzeitig durch die Lösung eines geometrischen und durch die Lösung eines dynamischen Problems entstanden. In diesem Abschnitt lernen wir die geometrische Deutung kennen.

Es sei \(f\) eine Funktion, die an der Stelle \(x_0\) differenzierbar ist und die Ableitung \(f'(x_0)\) besitzt. Die geometrische Deutung der Ableitung orientiert sich an der geometrischen Deutung des Differenzenquotienten. Der Differenzenquotient für das Intervall \([x_0,x]\) ist das Steigungsverhältnis der Funktion auf dem Intervall \([x_0,x]\). Verbindet man die Punkte \(P=(x_0,f(x_0))\) und \(Q=(x,f(x))\) durch eine Gerade, so entsteht eine Sekante des Funktionsgraphen, dh. eine Gerade, die den Funktionsgraphen in zwei Punkten schneidet (vgl. Abbildung 3.3).

Abbildung 3.3: Sekante eines Funktionsgraphen.

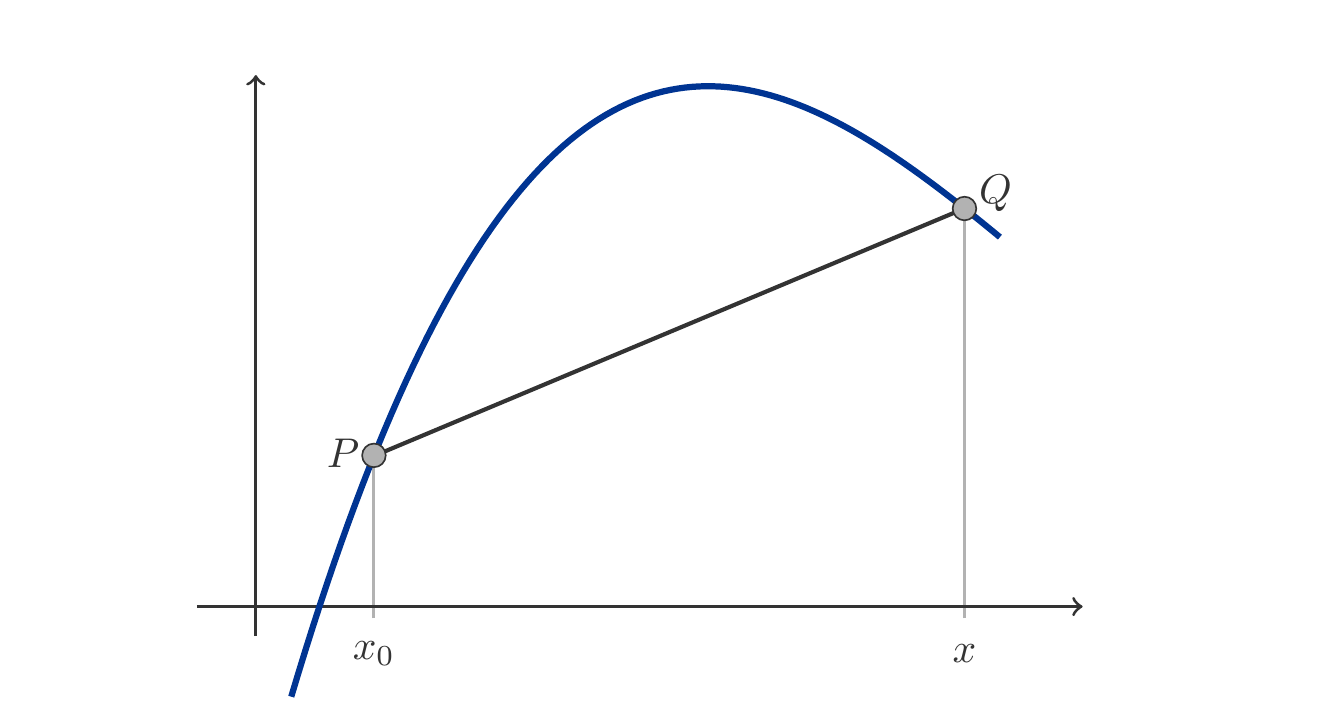
Wenn wir nun die \(x\)-Koordinate von \(Q\) eine Folge von Werten \(x_1,x_2,x_3,\ldots\) durchwandern lassen, die gegen \(x_0\) konvergiert, dann verändert sich die Sekante. Sie gewinnt immer mehr Ähnlichkeit mit der Tangente im Punkt \(P\), dh. mit der Geraden, die den Funktionsgraphen im Punkt \(P\) berührt. Der Vorgang ist in der Abbildung 3.4 veranschaulicht.

Abbildung 3.4: Grenzübergang beim Differenzenquotienten.

Die Tangente an den Funktionsgraphen im Punkt \(P=(x_0,f(x_0))\) ist eine Gerade, die durch den Punkt \(P\) geht. Unter den unendlich vielen Geraden, die ebenfalls durch den Punkt \(P\) gehen, ist die Tangente die einzige, deren Steigungsverhältnis mit der Ableitung \(f'(x_0)\) der Funktion \(f\) an der Stelle \(x_0\) übereinstimmt. Die Gleichung der Tangente lautet daher¹ \[ \begin{gathered} y=f'(x_0)(x-x_0)+f(x_0). \end{gathered} \tag{3.7}\] Wir können also als geometrische Deutung der Ableitung formulieren:

Satz 3.7 Die Ableitung einer differenzierbaren Funktion an einer Stelle \(x_0\) ist gleich der Steigung der Tangente an den Funktionsgraphen an der Stelle \(x_0\).

Existenz der Ableitung

Die eben diskutierten Beispiele und geometrischen Überlegungen mögen bei Leserinnen und Lesern den Eindruck erweckt haben, dass Funktionen, die eine Ableitung besitzen, nicht wirklich etwas Besonderes sind. Aber das trifft keinesfalls zu. Im Gegenteil: in Definition 3.2 werden zwei sehr strenge Bedingungen formuliert. Die Folge der Differenzenquotienten muss für jede gegen \(x_0\) strebende Zahlenfolge \(x_n\) konvergieren, und das immer gegen den gleichen Grenzwert. Dies ist keineswegs selbstverständlich.

Eine notwendige Voraussetzung für die Existenz der Ableitung einer Funktion ist ihre Stetigkeit. Stetigkeit ist ein Grundkonzept der modernen Mathematik, und es ist ein schwieriges Konzept. Daher wollen wir es hier dabei belassen, eine anschauliche Vorstellung zu entwickeln. Dabei bedienen wir uns bei Leonhard Euler, der 1748 geschrieben hat:

Eine Funktion ist stetig auf einem Intervall, wenn man dort ihren Graphen mit dem Bleistift zeichnen kann, ohne den Stift absetzen zu müssen.

Euler meinte damit, dass der Graph der Funktion keine Risse oder Löcher haben darf, dass kleine Änderungen der Variablen \(x\) nur kleine Änderungen des Funktionswertes \(f(x)\) bewirken. Die Funktion \(f(x)\) in Abbildung 3.5 ist im Punkt \(x=0\) nicht stetig. Sie besitzt dort eine Sprungstelle.

Abbildung 3.5: Eine Funktion mit einer Unstetigkeitstelle.

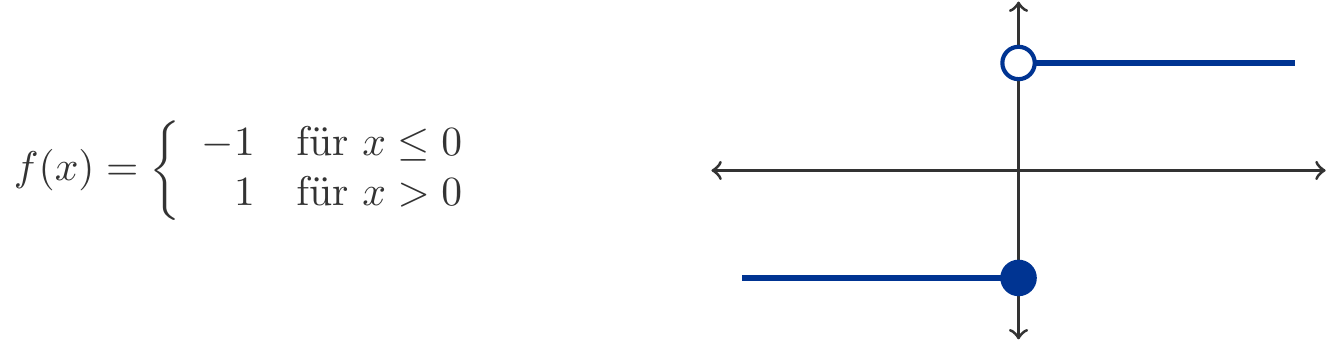
Funktionen der Art, wie sie in Abbildung 3.5 dargestellt wurde, sind keineswegs pathologische Ausnahmen. In Kapitel 5 werden wir Verteilungsfunktionen von diskreten Zufallsgrößen begegnen, die genau so ein Verhalten zeigen.

Doch Stetigkeit alleine reicht noch nicht aus. Damit eine Funktion in allen Punkten eines Intervalls differenzierbar ist, muss sie dort nicht nur stetig, sondern auch glatt sein. Was bedeutet das Attribut glatt in diesem Zusammenhang? Es heißt, dass eine Funktion zum Beispiel keine Knickstellen haben darf.

Abbildung 3.6: \(f(x)=|x|\) ist im Punkt \(x_0=0\) nicht differenzierbar.

Die scheinbar harmlose Funktion \(f(x)=|x|\) ist gar nicht so harmlos. Ihr Graph in Abbildung 3.6 passt in das Eulersche Bild der Stetigkeit. Aber in \(x_0=0\) besitzt \(f(x)\) einen Knick. Und es ist völlig offensichtlich: In diesem Punkt lässt sich die Lage der Tangente nicht eindeutig bestimmen. Tatsächlich ist jede lineare Funktion \(y=kx\) eine Tangente in \(x_0=0\), sofern \(-1\le k\le 1\) ist.

3.2 Differenzieren

Es sei \(y=f(x)\) eine Funktion, die auf einem Intervall \((a,b)\) differenzierbar ist. Um für jeden Punkt \(x\in(a,b)\) die Ableitung \(f'(x)\) auszurechnen, müssten wir für jedes \(x\) den Limes der Differenzenquotienten bilden. Aber es geht oft auch einfacher. Es gibt einfache Regeln, wie man die Ableitung einer elementaren Funktion als Formel angeben kann, ohne einen Limes bilden zu müssen. Diese sogenannten Regeln für das Differenzieren können mechanisch angewendet werden (Differentialkalkül) und daher auch Maschinen anvertraut werden.

Wir lernen in diesem Abschnitt die Regeln für das Differenzieren kennen und wir wollen auch imstande sein, sie bei einfachen Aufgaben anzuwenden. Es ist nicht das Wesen der Differentialrechnung, möglichst komplizierte Funktionsterme von Hand fehlerlos differenzieren zu können. Dies überlassen wir getrost Computerprogrammen. Wir wollen aber die Prinzipien verstehen, auf denen das Differenzieren beruht.

Die meisten Funktionsterme, mit denen man beim Differenzieren konfrontiert ist, bestehen aus sehr einfachen Bauteilen, die durch Operationen wie Addition und Multiplikation verknüpft sind. Außerdem entstehen Funktionsterme durch Verkettung, durch Bildung von inversen Funktionen und durch Bildung von Potenzen. Wenn wir wissen, wie man mit diesen Operationen beim Differenzieren umgeht, dann sind wir für viele Situationen gerüstet.

3.2.1 Elementare Ableitungsregeln

Beginnen wir mit Regeln, die wir schon kennen. Die Ableitung einer linearen Funktion \(f(x)=ax+b\) ist \(f'(x)=a\) für alle \(x\in\mathbb R\). Die Ableitung ist einfach das Steigungsverhältnis, das ja für eine lineare Funktion konstant ist. Der genaue Nachweis wurde im Beispiel 3.3 geführt. Für das Weitere sind zwei Spezialfälle von Bedeutung:

Satz 3.8 Die Ableitung einer konstanten Funktion \(f(x)=b\) ist \(f'(x)=0\) für alle \(x\in\mathbb R\).

Die Ableitung der Funktion \(f(x)=x\) ist \(f'(x)=1\) für alle \(x\in\mathbb R\).

Wir interessieren uns zunächst für all jene Funktionen, die wir aus linearen Funktionen durch Multiplikation und Addition neu gewinnen können. Zu diesem Zweck überlegen wir uns ganz allgemein, wie sich Addieren und Multiplizieren von Funktionstermen auf die Bildung von Ableitungen auswirken. Die Summenregel und die Produktregel beantworten diese Fragen.

Satz 3.9 (Summenregel) Sind \(y=f(x)\) und \(y=g(x)\) differenzierbare Funktionen, dann ist auch ihre Summe \(f(x)+g(x)\) eine differenzierbare Funktion und es gilt \[ \begin{gathered} (f(x)+g(x))'=f'(x)+g'(x). \end{gathered} \tag{3.8}\]

Man kann die Summenregel dadurch begründen, dass man einen genauen formalen Beweis führt, bei dem man die Differenzenquotienten untersucht und den Grenzübergang zur Ableitung laut Definition 3.2 führt. Wir verzichten aber auf diese Art des strengen Beweisens. Wir versuchen vielmehr, die Summenregel anschaulich zu verstehen, und das ist mindestens ebenso wichtig wie der formale Beweis. Ein anschauliches Verständnis erreicht man durch eine heuristische Überlegung².

Um die Summenregel zu verstehen, erinnern wir uns, dass wir bei kleinen Änderungen von \(x\) nach \(x+h\) die Änderung der Funktionswerte durch die Ableitung approximieren (näherungsweise ausrechnen) können: \[ \begin{gathered} \begin{array}{lcl} f(x+h)-f(x) &\approx& f'(x)h, \\ g(x+h)-g(x) &\approx& g'(x)h. \end{array} \end{gathered} \tag{3.9}\] Diese lokale Linearisierung ist überhaupt der Schlüssel für jeglichen intuitiven Umgang mit den Begriffen der Differentialrechnung. Wenn wir dann die Änderung der Summenfunktion \(f+g\) ausrechnen, ergibt sich durch Addition der beiden Gleichungen in (3.9): \[ \begin{aligned} & \left[f(x+h) + g(x+h)\right] - \left[f(x)+g(x) \right] \\ = & \left[f(x+h)-f(x) \right] + \left[g(x+h)-g(x) \right]\\ \approx & \left[f'(x)+g'(x) \right]h. \end{aligned} \] Wir sehen: Weil die Änderung einer Summe gleich ist der Summe der Änderungen der Glieder, ist es plausibel, dass auch die Ableitung einer Summe gleich ist mit der Summe der Ableitungen.

Wir sehen uns einen einfachen, aber wichtigen Spezialfall an.

Beispiel 3.10 (Additive Konstante)

Es sei \(y=f(x)\) eine differenzierbare Funktion und es sei \(c\in\mathbb R\) eine Zahl. Wie lautet die Ableitung von \(h(x)=f(x)+c\)?

Die Antwort findet man leicht mit der Summenregel. Die Funktion \(h\) ist ja eine Summe von zwei differenzierbaren Funktionen. Daher gilt \[ \begin{gathered} h'(x)=(f(x)+c)'=f'(x)+(c)'=f'(x)+0=f'(x). \end{gathered} \] Damit ist klar: Eine additive Konstante verschwindet beim Differenzieren.

Die Produktregel ist etwas komplizierter als die Summenregel. Wir beginnen mit einer heuristischen Überlegung um zu verstehen, was überhaupt passiert.

Beispiel 3.11

Es seien \(A,\,a,\,B,\,b\) irgendwelche Zahlen. Es ist uns geläufig, dass \[ \begin{gathered} (A+a)(B+b)=AB+aB+Ab+ab. \end{gathered} \tag{3.10}\] Jetzt stellen wir uns vor, dass \(A\) und \(B\) zwei Zahlen sind, die im Vergleich zu \(a\) und \(b\) sehr groß sind. Also z.B. \(A=1000\), \(B=3000\), \(a=15\) und \(b=20\). Wir interessieren uns für den Unterschied der Produkte \((A+a)(B+b)\) und \(AB\). Für unser Zahlenbeispiel können wir den Unterschied einfach ausrechnen: \[ \begin{gathered} (A+a)(B+b)-AB=3065300-3000000=65300. \end{gathered} \] Wenn wir aber allgemein wissen wollen, aus welchen Bestandteilen sich diese Differenz zusammensetzt, müssen wir (3.10) anwenden und erhalten \[ \begin{gathered} (A+a)(B+b)-AB=aB+Ab+ab, \end{gathered} \] und in unserem Zahlenbeispiel \[ \begin{gathered} 65300=45000+20000+300. \end{gathered} \] Wir sehen daraus, dass der dritte Summand \(ab\) wenig beiträgt. Die bestimmenden Anteile sind \(aB\) und \(Ab\), also \[ \begin{gathered} (A+a)(B+b)-AB\approx aB+Ab. \end{gathered} \] Die Abbildung 3.7 zeigt diesen Sachverhalt sehr anschaulich.

Wir werden sehen, dass die Produktregel für das Differenzieren genau nach dieser Formel erfolgt: Änderung des ersten Faktors mal Wert des zweiten Faktors plus Wert des ersten Faktors mal Änderung des zweiten Faktors.

Abbildung 3.7: Zur Produktregel.

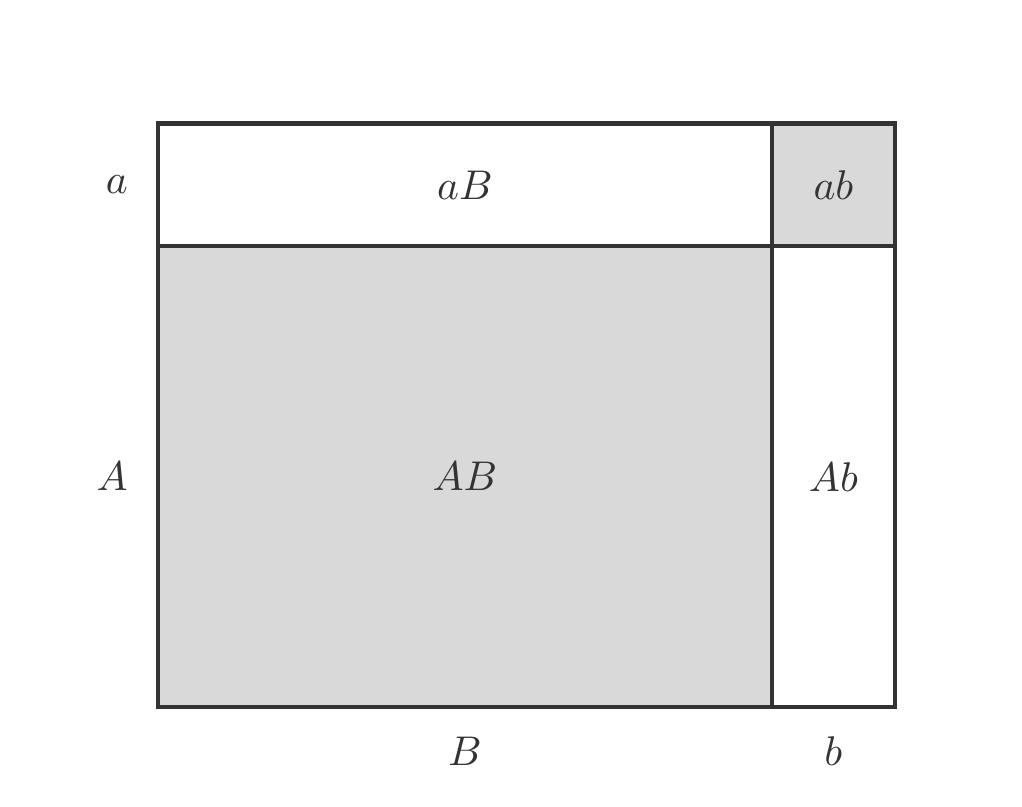
Wir nehmen wieder an, dass wir es mit Funktionen zu tun haben, für die die Gleichungen (3.9) gelten, die wir aber jetzt leicht verändert in der Form \[ \begin{gathered} \begin{array}{lcl} f(x+h) &\approx& f(x)+f'(x)h, \\ g(x+h) &\approx& g(x)+g'(x)h. \end{array} \end{gathered} \] schreiben. Wenn wir nun die Änderung der Produktfunktion \(fg\) ausrechnen, ergibt sich \[ \begin{aligned} & f(x+h)g(x+h) \\ \approx & [f(x)+f'(x)h][g(x)+g'(x)h]\\ = & f(x)g(x)+f'(x)g(x)h+f(x)g'(x)h+f'(x)g'(x)h^2. \end{aligned} \] Die geometrische Interpretation dieser Entwicklung eines Produkts in vier Summanden ist in der Abbildung 3.7 angedeutet. Da wir es immer mit kleinen Änderungen \(h\) zu tun haben, ist \(h^2\) besonders klein und daher ist der vierte Summand vernachlässigbar. Wir erhalten also schließlich \[ \begin{gathered} f(x+h)g(x+h)-f(x)g(x)\approx [f'(x)g(x)+f(x)g'(x)]h \end{gathered} \] Dies führt uns zur Vermutung, dass die Ableitung des Produkts \(f(x)g(x)\) gleich \(f'(x)g(x)+f(x)g'(x)\) sein müsste.

Satz 3.12 (Produktregel) Sind \(y=f(x)\) und \(y=g(x)\) differenzierbare Funktionen, dann ist auch ihr Produkt \(f(x)\cdot g(x)\) eine differenzierbare Funktion und es gilt \[ \begin{gathered} \ [f(x)g(x)]'=f'(x)g(x)+f(x)g'(x). \end{gathered} \tag{3.11}\]

Wir sehen uns wieder einen sehr einfachen, aber wichtigen Spezialfall an.

Beispiel 3.13 (Konstanter Faktor)

Es sei \(y=f(x)\) eine differenzierbare Funktion und es sei \(c\in\mathbb R\) eine Zahl. Wie lautet die Ableitung von \(h(x)=cf(x)\)?

Die Antwort findet man leicht mit der Produktregel. Die Funktion \(h(x)\) ist ja ein Produkt von zwei differenzierbaren Funktionen. Daher gilt \[ \begin{gathered} \begin{array}{rcrcll} h'(x)=[cf(x)]' & = & (c)' f(x) & + & cf'(x) & \\ & = & 0\;\;f(x) & + & cf'(x) & = cf'(x). \end{array} \end{gathered} \] Damit ist klar: Ein konstanter Faktor bleibt beim Differenzieren unverändert erhalten.

Diese beiden Regeln, die Summenregel und die Produktregel, reichen aus, eine große Zahl von Funktionen, insbesondere alle Polynome, erfolgreich zu differenzieren.

Das nächste Beispiel ist eigentlich nicht mehr ein Spezialfall der Produktregel, sondern eine eigenständige Regel für das Differenzieren. Es geht um Potenzfunktionen mit positiven ganzzahligen Exponenten.

Beispiel 3.14 (Ableitung von Potenzfunktionen)

Wir wollen \(f(x)=x^n\) mit natürlichen Exponenten \(n\in\mathbb N\) differenzieren. Einen Spezialfall davon kennen wir schon. Für \(n=1\) ist \(f(x)=x\) und es gilt \(f'(x)=1\).

Untersuchen wir nun die Funktion \(f(x)=x^2\). Der Differenzenquotient lautet \[ \begin{gathered} \frac{f(x+h)-f(x)}{h}=\frac{(x+h)^2-x^2}{h}=2x+h. \end{gathered} \] Nach dem Grenzübergang \(h\to 0\) ergibt sich \(f'(x)=2x\).

Wir behaupten nun, die allgemeine Regel für die Ableitung von Potenzfunktionen lautet \[ \begin{gathered} f(x)=x^n \quad\Rightarrow\quad f'(x)=nx^{n-1}. \end{gathered} \tag{3.12}\] Wie wir gesehen haben, ist diese Regel sicher für die Fälle \(n=1\) und \(n=2\) richtig. Wir beweisen sie nun für den Fall \(n=3\). Dazu verwenden wir die Produktregel: \[ \begin{gathered} (x^3)'=(x^2\cdot x)'=(x^2)'x+x^2(x)'=2x\cdot x+x^2\cdot 1=3x^2. \end{gathered} \] Also stimmt unsere Regel auch für \(n=3\). Man kann nun so weitergehen, um die Regel für alle \(n\in\mathbb N\) nachzuweisen. Wenn wir sie für \(n=k-1\) nachgewiesen haben, dann folgt automatisch nach der Produktregel \[ \begin{aligned} (x^k)' = (x^{k-1}\cdot x)' & = (x^{k-1})'x+x^{k-1}(x)' \\ & = (k-1)x^{k-2}\cdot x+x^{k-1}\cdot 1=kx^{k-1}. \end{aligned} \] Also ist die Regel dann auch für \(n=k\) richtig.

Nun sind wir in der Lage, beliebige Polynome zu differenzieren: \[ \begin{gathered} \begin{array}{ll} f(x)=a & f'(x)=0\\ f(x)=ax+b & f'(x)=a\\ f(x)=ax^2+bx+c &f'(x)=2ax+b\\ \ldots \end{array} \end{gathered} \]

Wenn ein Funktionsterm als Produkt von zwei Funktionen darstellbar ist, dann ist es meist einfacher, die Produktregel direkt anzuwenden als den Funktionsterm zu entwickeln (auszumultiplizieren).

Musteraufgabe 3.15 Gesucht ist die Ableitung der Funktion \(h(x)=x^4(5x^2-1)\).

Lösung: Wir setzen \(f(x)=x^4\) und \(g(x)=5x^2-1\). Dann gilt \[ \begin{aligned} h'(x) & =f'(x)g(x)+f(x)g'(x) \\ & =4x^3(5x^2-1)+x^4\cdot 10x=30x^5-4x^3. \end{aligned} \] □

Wir beenden unser Anwendungen der Produktregel mit einem Beispiel, dessen Lösung wir schon kennen.

Beispiel 3.16 (Ableitung von \(f(x)=1/x\))

Wir wissen aus dem Beispiel 3.5, dass die Funktion \(f(x)=1/x\) für \(x\not=0\) differenzierbar ist und wie die Ableitung aussieht. Es ist aber interessant zu sehen, wie man die Ableitung auch mit der Produktregel finden kann.

Es ist ja \(xf(x)=1\) und wenn wir auf beiden Seiten der Gleichung differenzieren, müssen wir identische Ableitungen erhalten. Also ist \[ \begin{gathered} (xf(x))'=(1)'=0, \end{gathered} \] und daher \[ \begin{gathered} 1f(x)+xf'(x)=0. \end{gathered} \] Aus dieser Gleichung können wir \(f'(x)\) ausrechnen und erhalten \[ \begin{gathered} f'(x)=-\frac{f(x)}{x}=-\frac{1}{x^2}. \end{gathered} \tag{3.13}\]

3.2.2 Die Kettenregel

Addition und Multiplikation sind nicht die einzigen Operationen, um aus gegebenen Funktionstermen neue zu bilden. Die Verkettung von Termen spielt eine ebenso große Rolle.

Verketten bedeutet, eine Funktion in eine andere einzusetzen. Wenn wir also zwei Funktionen \(z=f(y)\) und \(y=g(x)\) haben, dann können wir die Verkettung \(f(g(x))\) dadurch bilden, dass wir \(y\) in \(f(y)\) durch \(g(x)\) ersetzen. Die Funktion \(f(y)\), in die eingesetzt wird, nennen wir die äußere Funktion, die Funktion, die eingesetzt wird, heißt innere Funktion.

Wenn beispielsweise \(f(y)=\sqrt{y}\) und \(g(x)=1+x^2\), dann ist \[ \begin{gathered} f(g(x))=\sqrt{g(x)}=\sqrt{1+x^2}. \end{gathered} \] Beachten Sie, dass das Verketten nicht kommutativ ist. In unserem Beispiel ergibt sich: \[ \begin{gathered} g(f(y))=1+(f(y))^2=1+(\sqrt{y})^2 =1+y. \end{gathered} \]

Die folgende Kettenregel ist genau dafür gedacht solche Verkettungen zu differenzieren. Sie ist sicherlich die wichtigste und folgenreichste Regel für die Bildung von Ableitungen.

Bevor wir die Kettenregel als Lehrsatz formulieren, versuchen wir wieder, das Problem heuristisch in den Griff zu bekommen. Beginnen wir mit einem Beispiel.

Beispiel 3.17 (Kettenregel für lineare Funktionen)

Es seien \(f(y)=ay+b\) und \(g(x)=cx+d\) zwei lineare Funktionen. Es ist klar, dass \(f'(y)=a\) und \(g'(x)=c\). Wir verketten die beiden Funktionen und erhalten so \[ \begin{gathered} f(g(x))=f(cx+d)=a(cx+d)+b=acx+ad+b. \end{gathered} \] Das Ergebnis der Verkettung ist eine lineare Funktion mit dem Steigungsverhältnis \(ac\), also \([f(g(x)]'=ac\). Wir stellen somit fest, dass im Fall von linearen Funktionen \[ \begin{gathered} \ [f(g(x))]'=f'(y)g'(x) \end{gathered} \] gilt. Es wird sich herausstellen, dass diese Formel ganz allgemein auch für nichtlineare Funktionen richtig ist.

Es seien \(z=f(y)\) und \(y=g(x)\) zwei differenzierbare Funktionen, die sich zu \(f(g(x))\) verketten lassen. Wir gehen wieder davon aus, dass für kleine Veränderungen \(h\) und \(k\) lineare Approximationen durch die Ableitungen \[ \begin{gathered} \begin{array}{lcl} f(y+h) &\approx& f(y)+f'(y)h,\\ g(x+k) &\approx& g(x)+g'(x)k \end{array} \end{gathered} \] möglich sind. Wenn wir jetzt die verkettete Funktion \(f(g(x))\) an der Stelle \(x+k\) untersuchen, dann sehen wir, dass \[ \begin{gathered} f(g(x+k))\approx f(g(x)+g'(x)k). \end{gathered} \] Nun übernimmt \(g(x)\) die Rolle von \(y\) und \(g'(x)k\) die Rolle von \(h\). So ergibt sich weiter \[ \begin{gathered} \begin{array}{lcl} f(g(x+k))&\approx& f(g(x)+g'(x)k)\\ &=& f(y+h)\approx f(y)+f'(y)h\\ &=& f(g(x))+f'(g(x))g'(x)k. \end{array} \end{gathered} \] Das heißt ganz einfach, dass \[ \begin{gathered} f(g(x+k))- f(g(x))\approx f'(g(x))g'(x)\cdot k. \end{gathered} \] Kandidat für die Ableitung von \(f(g(x))\) ist also das Produkt der äußeren Ableitung \(f'\) und der inneren Ableitung \(g'\).

Satz 3.18 (Kettenregel) Es seien \(z=f(y)\) und \(y=g(x)\) zwei differenzierbare Funktionen, die sich zu \(f(g(x))\) verketten lassen. Dann ist auch die verkettete Funktion differenzierbar und es gilt \[ \begin{gathered} \ [f(g(x))]'=f'(g(x))\cdot g'(x). \end{gathered} \tag{3.14}\] Die Kettenregel hat also eine sehr einfache Struktur. Sie besagt folgendes:

Die Ableitung eines verketteten Funktionenpaars ist gleich dem Produkt der Ableitungen der einzelnen Funktionen.

Musteraufgabe 3.19 Differenziere die Funktion \(h(x)=(1+x^2)^{10}\).

Lösung: Wir setzen \(f(y)=y^{10}\) und \(y=g(x)=1+x^2\). Dann ist \(h(x)=f(g(x))=g^{10}(x)\) und es folgt \[ \begin{gathered} h'(x)=f'(g(x))g'(x)=10g^{9}(x)\cdot 2x= 20x(1+x^2)^{9}. \end{gathered} \] □

Beispiel 3.20 (Ableitung eines Kehrwerts)

Es sei \(g\not=0\) eine differenzierbare Funktion. Wir wollen die Funktion \[ \begin{gathered} h(x)=\frac{1}{g(x)} \end{gathered} \] differenzieren. Hierzu verwenden wir die Kettenregel. Setzen wir \(y=g(x)\) und \(\displaystyle f(y)=1/y\), so ist \(h(x)=f(g(x))\). Daraus folgt nach (3.13) \[ \begin{gathered} h'(x)=f'(g(x))g'(x)=-\frac{g'(x)}{g^2(x)}. \end{gathered} \tag{3.15}\]

Beispiel 3.21 (Potenzen mit negativen Exponenten)

Wir wollen die Ableitung von \(\displaystyle f(x)=1/x^n\) für \(n\in\mathbb N\) bilden. Unter Verwendung von (3.15) ergibt sich \[ \begin{gathered} f'(x)=-\frac{nx^{n-1}}{x^{2n}}=-\frac{n}{x^{n+1}}=-nx^{-n-1}. \end{gathered} \]

Beispiel 3.22 (Quotientenregel)

Die Quotientenregel gibt an, wie sich die Ableitung eines Quotienten \(f(x)/g(x)\) aus den Ableitungen von Zähler und Nenner zusammensetzt. Es gilt \[ \begin{gathered} \left( \frac{f(x)}{g(x)} \right)'=\frac{f'(x)g(x)-f(x)g'(x)}{g^2(x)}. \end{gathered} \tag{3.16}\] Diese Regel folgt aus der Produktregel und aus (3.15). Es ist \[ \begin{gathered} \left( \frac{f}{g} \right)'=\left( f\frac{1}{g} \right)'= f'\frac{1}{g}+f\left(\frac{1}{g}\right)' =\frac{f'}{g}-f\frac{g'}{g^2}=\frac{f'g-fg'}{g^2}. \end{gathered} \]

Musteraufgabe 3.23 Differenziere die Funktion \(\displaystyle h(x)=(3x-2)/(x+1)\) nach der Quotientenregel.

Lösung: Es ist \(f(x)=3x-2\) und \(g(x)=x+1\). \[ \begin{gathered} h'(x)=\frac{3(x+1)-(3x-2)\cdot 1}{(x+1)^2}=\frac{5}{(x+1)^2}. \end{gathered} \] □

Mit der Kettenregel können wir auch inverse Funktionen differenzieren, wenn wir die Ableitung der Ursprungsfunktion kennen.

Beispiel 3.24 (Ableitung einer inversen Funktion)

Es seien \(y=f(x)\) und \(x=g(y)\) stetige und zueinander inverse Funktionen. Beispiele für solche zueinander inversen Funktionenpaare sind uns schon lange bekannt. Etwa: \[ \begin{gathered} y=x^2,\quad x=\sqrt{y},\\ y=e^x,\quad x=\ln y. \end{gathered} \] Wir nehmen an, dass \(f\) eine differenzierbare Funktion ist. Bevor wir daran gehen können, eine Ableitung der inversen Funktion zu berechnen, müssen wir einen Augenblick darüber nachdenken, ob die inverse Funktion überhaupt differenzierbar ist.

Wir machen das auf anschauliche heuristische Weise. Die Differenzierbarkeit der inversen Funktion \(g\) kann nur daran scheitern, dass Knickstellen oder vertikale Tangenten auftreten. Knickstellen können aber nicht auftreten, weil die Graphen von \(f\) und \(g\) identisch sind und der Graph von \(f\) keine Knickstellen besitzt. Eine vertikale (dh. zur \(x\)-Achse parallele!) Tangente tritt beim Graphen von \(x=g(y)\) dort auf, wo der Graph von \(y=f(x)\) eine horizontale Tangente besitzt, also wo \(f'(x)=0\) ist. Solche Punkte sind daher auszuschließen.

Also ist \(g\) an allen Punkten \(y=f(x)\) differenzierbar, wo \(f'(x)\not=0\) ist. Aus \(f(g(y))=y\) folgt durch beidseitige Bildung der Ableitungen \[ \begin{gathered} f'(g(y))g'(y)=1, \end{gathered} \] und daher \[ \begin{gathered} g'(y)=\frac{1}{f'(g(y))}=\frac{1}{f'(x)},\quad \mbox{wobei $x=g(y)$ und $y=f(x)$.} \end{gathered} \tag{3.17}\] Wir sehen: Die Ableitung der inversen Funktion ist der Kehrwert der Ableitung der Ursprungsfunktion.

Beispiel 3.25 (Ableitung von \(g(x)=\sqrt{x}\))

Wir kennen die Ableitung von \(g(x)=\sqrt{x}\) aus dem Beispiel 3.6. Das gleiche Ergebnis können wir aber auch auf einem anderen Weg erhalten.

Die Funktion \(g\) ist die inverse Funktion von \(x=f(y)=y^2\) mit der Ableitung \(f'(y)=2y\). Daraus folgt \[ \begin{gathered} g'(x)=\frac{1}{f'(g(x))}=\frac{1}{2g(x)}=\frac{1}{2\sqrt{x}}. \end{gathered} \]

3.2.3 Exponentialfunktion und Logarithmus

Zuletzt müssen wir uns noch mit der Ableitung von Exponentialfunktionen und Logarithmusfunktionen beschäftigen. Der grundlegende Satz, aus dem sich alles weitere wie von selbst ergibt, ist die Ableitungsregel für die Exponentialfunktion \(f(x)=\exp(x)=e^x\).

Satz 3.26 Die Exponentialfunktion \(f(x)=\exp(x)=e^x\) ist differenzierbar und es gilt \[ \begin{gathered} f'(x)=\exp(x)=e^x. \end{gathered} \tag{3.18}\]

Die Exponentialfunktion \(\exp(x)=e^x\) reproduziert sich also beim Differenzieren selbst. Das ist eine bemerkenswerte Eigenschaft. Man kann sogar nachweisen, dass es keine andere Funktion gibt, die das gleiche leistet. Uns interessiert aber vor allem, woran es liegt, dass die Exponentialfunktion diese schöne Eigenschaft besitzt. Und das heuristisch zu verstehen, ist gar nicht schwierig. Wir wissen ja, dass \[ \begin{gathered} e^x=\lim_{n\to\infty} \Big(1+\frac{x}{n}\Big)^n. \end{gathered} \tag{3.19}\] Es liegt daher nahe zu vermuten, dass sich Eigenschaften von \(e^x\) aus den Eigenschaften der Folge von Funktionen \[ \begin{gathered} g_n(x)=\Big(1+\frac{x}{n}\Big)^n \end{gathered} \] erklären lassen. Wenn wir die Funktionen \(g_n(x)\) differenzieren, dann erhalten wir (mit der Kettenregel) \[ \begin{gathered} g_n'(x)=n\Big(1+\frac{x}{n}\Big)^{n-1}\frac{1}{n}= \Big(1+\frac{x}{n}\Big)^{n-1}=\frac{g_n(x)}{1+\dfrac{x}{n}}\,. \end{gathered} \] Die Funktion \(g_n(x)\) reproduziert sich also fast beim Differenzieren, und die Abweichung von der exakten Reproduktion wird mit wachsendem \(n\) immer geringer. Zusammen mit (3.19) ist das zwar kein strenger Beweis von Satz 3.26, aber doch ein Hinweis darauf, dass die Aussage von Satz 3.26 nicht gänzlich unverständlich ist.

In den allermeisten Anwendungen freilich begegnet uns die Exponentialfunktion in verketteter Form, d.h. wir haben es mit Funktionen der Form \(y=e^{f(x)}\) zu tun. Deren Ableitung muss natürlich mit Hilfe der Kettenregel gebildet werden. Die äußere Ableitung ergibt sich dabei aus Satz 3.26:

Satz 3.27 Es sei \(g(x)=e^{f(x)}=e^y\) mit \(y=f(x)\). Dann ist: \[ \begin{gathered} g'(x)=e^y\cdot y'=e^{f(x)}\cdot f'(x)\,. \end{gathered} \tag{3.20}\]

Musteraufgabe 3.28 Differenziere \(f(x)=3e^{-5x^2}\).

Lösung: Um die Ableitung von \(f\) zu finden, wenden wir die Kettenregel (3.20) an: \[ \begin{gathered} f'(x)=3e^{-5x^2}(-10x)=-30xe^{-5x^2}. \end{gathered} \] □

Nun der allgemeine Fall.

Beispiel 3.29 (Exponentialfunktionen)

Es sei nun \(f(x)=a^x\) eine Exponentialfunktion mit einer beliebigen positiven Basis. Wir wissen aus (2.37), dass wir eine solche Exponentialfunktion in der Form \[ \begin{gathered} f(x)=a^x=e^{x\ln a} \end{gathered} \tag{3.21}\] schreiben können. In dieser Form ist es nicht schwierig, die Ableitung zu berechnen. Wir wenden die Kettenregel an und es ergibt sich \[ \begin{gathered} f'(x)=e^{x\ln a}\ln a=a^x\ln a. \end{gathered} \tag{3.22}\]

Musteraufgabe 3.30 Gesucht ist die 1. Ableitung der Funktion \(y=3^{x^2+1}\).

Lösung: Wir beginnen damit, \(y\) als Eulersche Exponentialfunktion zu schreiben, sodass wir (3.20) anwenden können: \[ \begin{gathered} y=3^{x^2+1}=e^{(x^2+1)\ln 3} \end{gathered} \] Mittels der Kettenregel ergibt sich: \[ \begin{gathered} y'=e^{(x^2+1)\ln 3}\cdot 2x\cdot\ln 3=2x\ln 3\cdot 3^{x^2+1} \end{gathered} \] □

Die Ableitung der Logarithmusfunktion \(g(x)=\ln x\) ergibt sich durch die Kettenregel.

Beispiel 3.31 (Ableitung von \(g(x)=\ln x\))

Es sei \(g(x)=\ln x\). Dann ist \(e^{g(x)}=x\) und daher durch Bilden der Ableitung auf beiden Seiten: \[ \begin{gathered} e^{g(x)}g'(x)=1. \end{gathered} \] Daraus folgt \[ \begin{gathered} g'(x)=\frac{1}{e^{g(x)}}=\frac{1}{e^{\ln x}}=\frac{1}{x}. \end{gathered} \tag{3.23}\]

Wie die Exponentialfunktion tritt uns auch die Logarithmusfunktion in den allermeisten Anwendungen in verketteter Form gegenüber. Die Kettenregel zusammen mit (3.23) löst das Problem.

Satz 3.32 (Logarithmische Ableitung) Es sei \(g(x)=\ln f(x)=\ln y\) mit \(y=f(x)\). Dann ist: \[ \begin{gathered} g'(x)=\left(\ln f(x)\right)'=\frac{f'(x)}{f(x)}. \end{gathered} \tag{3.24}\]

Musteraufgabe 3.33 Gesucht ist die erste Ableitung von \(y=\ln(3x^2-4x+1)\).

Lösung: Dieses \(y\) ist genau von der Form \(\ln f(x)\) mit \(f(x)=3x^2-4x+1\). Mittels (3.24) finden wir: \[ \begin{gathered} y'=\frac{6x-4}{3x^2-4x+1}. \end{gathered} \] □

Als letzte Ableitungsregel fehlt uns noch das Differenzieren von allgemeinen Potenzfunktionen \(f(x)=x^{\alpha}\). Bisher können wir die Ableitung \(f'(x)\) lediglich für ganzzahliges \(\alpha\) bilden, siehe (3.12).

Die allgemeine Regel sieht genauso aus wie im Fall ganzzahliger Exponenten.

Satz 3.34 (Ableitung von Potenzfunktionen) Es sei \(f(x)=x^\alpha\) mit \(\alpha\in\mathbb R\). Dann gilt: \[ \begin{gathered} f'(x)=\alpha x^{\alpha-1}. \end{gathered} \tag{3.25}\]

Begründung: Man sieht das leicht, wenn wir \(x^\alpha\) als Exponentialfunktion schreiben. Es ist ja \(f(x)=x^\alpha=e^{\alpha\ln\,x}.\) Daraus folgt mit der Kettenregel \[ \begin{gathered} f'(x)=e^{\alpha\ln\,x}\,\alpha\,\frac{1}{x}=x^\alpha\,\alpha\,\frac{1}{x}= \alpha x^{\alpha-1}. \end{gathered} \] □

Wir beschließen diesen Abschnitt mit einem letzten Beispiel:

Musteraufgabe 3.35 Gesucht ist die erste Ableitung der Funktion \(y=x^x\).

Lösung: Wieder beginnen wir damit, \(y\) als Eulersche Exponentialfunktion zu schreiben: \[ \begin{gathered} y=x^x = e^{x\ln x}. \end{gathered} \] Mittels (3.20) und der Produktregel für die innere Ableitung ergibt sich: \[ \begin{aligned} y'&=e^{x\ln x}\left(x\ln x\right)'= e^{x\ln x}\left(1\cdot\ln x+x\cdot\frac{1}{x}\right)\\[4pt] &=x^x\left(\ln x +1\right). \end{aligned} \] □

3.3 Interpretationen der Ableitung

3.3.1 Geschwindigkeit

Die dynamische Interpretation der Ableitung hängt mit dem Begriff der Geschwindigkeit zusammen. Es sei \(y=f(t)\) eine Funktion, die einen Zustand eines Gegenstands oder eines Systems angibt. Dabei bezeichne \(t\) den Zeitpunkt, zu dem der Zustand gemessen wird.

Ortsveränderung

Ein Fahrzeug bewegt sich entlang einer Straße. Es startet zum Zeitpunkt \(t_0\) an einem bestimmten Punkt, der die Kilometermarkierung \(f(t_0)\) trägt. Zu jedem Zeitpunkt \(t>t_0\) sei \(f(t)\) die Kilometermarkierung jenes Punktes der Straße, an dem sich das Fahrzeug zu diesem Zeitpunkt befindet.

Wenn die Zeitdauer \(t-t_0\) verstrichen ist, dann hat das Fahrzeug die Strecke \(f(t)-f(t_0)\) zurückgelegt. Der Differenzenquotient \[ \begin{gathered} \frac{f(t)-f(t_0)}{t-t_0} \end{gathered} \] gibt an, wie groß die Strecke war, die das Fahrzeug durchschnittlich in einer Zeiteinheit zurückgelegt hat. Man nennt diesen Differenzenquotienten die durchschnittliche Geschwindigkeit des Fahrzeugs im Zeitintervall \([t_0,t]\).

Man sagt, das Fahrzeug bewegt sich gleichförmig, wenn der zurückgelegte Weg \(f(t)\) eine lineare Funktion ist, also \(f(t)=vt+b\). In diesem Fall ist für jedes Zeitintervall der Differenzenquotient und damit die Durchschnittsgeschwindigkeit gleich \(v\). Es ist dann gerechtfertigt, \(v\) als die Geschwindigkeit des Fahrzeugs zu bezeichnen.

Bewegt sich das Fahrzeug nicht gleichförmig, dann ist der zurückgelegte Weg \(f(t)\) irgendeine nichtlineare Funktion. Die Durchschnittsgeschwindigkeit kann dann für verschiedene Intervalle unterschiedlich sein. Wie soll man in einer solchen Situation die Geschwindigkeit des Fahrzeugs zu einem bestimmten Zeitpunkt definieren?

Die Antwort auf diese Frage ist der Begriff der momentanen Geschwindigkeit. Wir nehmen an, dass die Funktion \(y=f(t)\) differenzierbar ist. Dann berechnen wir die Durchschnittgeschwindigkeiten für immer kleinere Intervalle \([t_0,t]\). Der Grenzwert dieser Durchschnittsgeschwindkeiten ist die Ableitung \[ \begin{gathered} f'(t_0)=\lim_{t\to t_0} \frac{f(t)-f(t_0)}{t-t_0} \end{gathered} \] der Funktion \(f\) an der Stelle \(t_0\). Diesen Grenzwert nennt man die momentane Geschwindigkeit des Fahrzeugs zum Zeitpunkt \(t_0\). Die Momentangeschwindigkeit ist also die Ableitung der Funktion, die den zurückgelegten Weg angibt.

3.3.2 Änderungsraten

Wenden wir uns wieder der allgemeinen Situation zu. Der Differenzenquotient \[ \begin{gathered} \frac{f(t)-f(t_0)}{t-t_0} \end{gathered} \tag{3.26}\] gibt die durchschnittliche Änderung des Zustandes im Zeitintervall \([t_0,t]\) an. Eine solche Maßzahl, die die Änderung auf die dafür benötigte Zeit bezieht, nennt man allgemein eine Änderungsrate oder einfach eine Rate. So gesehen ist die Geschwindigkeit eines Fahrzeugs die Rate der Ortsveränderung. Unter der momentanen Änderungsrate versteht man dann die Ableitung der Zustandsfunktion \(f\), also \[ \begin{gathered} f'(t_0)=\lim_{t\to t_0}\frac{f(t)-f(t_0)}{t-t_0}. \end{gathered} \tag{3.27}\] Wir fassen zusammen:

Satz 3.36 Die Ableitung einer differenzierbaren Funktion \(f(t)\) an einer Stelle \(t_0\) ist die momentane Änderungsrate der Funktion an der Stelle \(t_0\).

Musteraufgabe 3.37 Zwischen \(1990\) und \(2010\) konnte ein Unternehmen seinen Umsatz beträchtlich steigern. Eine statistische Analyse der jährlichen Umsätze ergab, dass sich diese in guter Näherung durch die Funktion \[ \begin{gathered} f(t)= 5+0.1t+0.01t^2 \quad\text{in Millionen GE},\quad 1990: t=0. \end{gathered} \] beschreiben lassen.

• Wie groß war das durchschnittliche Umsatzwachstum zwischen \(1995\) und \(2000\)?

• Wie hoch war die (momentane) Zuwachsrate \(1998\)?

Bevor wir uns an die Beantwortung dieser Fragen machen, ein Wort zur gegebenen Funktion \(f(t)=5+0.1t+0.01t^2\). Sie ist ein Beispiel für eine quadratische Trendfunktion. Wenn wir die Jahresumsätze in ein 2-dimensionales Koordinatensystem zeichnen, erhalten wir das Bild eine Punktwolke \((t_i, f(t_i))\), \(t_i\) das Jahr \(i\), \(f(t_i)\) der Umsatz des Jahres \(t_i\). Nun kann man mittels Verfahren, die Statistik und Ökonometrie zur Verfügung stellen, durch diese Punktwolke eine Trendfunktion legen, die die Punkte möglichst gut anpasst, siehe Abbildung 3.8 zur Illustration.

Abbildung 3.8: Anpassung einer Trendfunktion in Musteraufgabe 3.37.

Der Sinn dieser Trendfunktionen ist einerseits einfache Erklärungsmodelle (etwa für die Umsatzentwicklung) zu haben, andererseits können sie auch für Prognosen verwendet werden.

Lösung:

(a) Wir untersuchen die Funktion \(f(t) = 5 +0.1\;t + 0.01\;t^{2}\). Das durchschnittliche Wachstum im Intervall \([t_{0},t]\) wird durch den Differenzenquotienten \[ \begin{gathered} \dfrac{f(t)-f(t_{0})}{t-t_0} \end{gathered} \] angegeben. Zuerst ermitteln wir: \[ \begin{gathered} \begin{array}{crlcrlcl} 1995&\widehat{=} & t_{0}&=&5 :& f(t_{0})&=&5+0.1\cdot 5+0.01\cdot 5^2=5.75, \\ 2000&\widehat{=} & t&=&10 :&f(t) &=&5+0.1\cdot 10+0.01\cdot 10^2=7. \\ \end{array} \end{gathered} \] Nun berechnen wir den Differenzenquotienten: \[ \begin{gathered} \dfrac{f(t)-f(t_{0})}{t-t_0} = \dfrac{7-5.75}{10-5} = 0.25\,. \end{gathered} \] Die Umsätze wuchsen daher im Zeitraum 1995–2000 durchschnittlich um \(0.25\) Millionen GE /Jahr.

(b) Die momentane Zuwachsrate an der Stelle \(t\) wird durch die Ableitung \(f'(t)\) gegeben. Wir berechnen ihren Wert für das Jahr \(1998\), also für \(t=8\): \[ \begin{aligned} f'(t) &= 0.1 + 2\cdot0.01t\;\implies f'(8) = 0.1 + 0.02\cdot8 =0.26\,. \end{aligned} \] Im Jahr 1998 betrugt die momentane Wachstumsrate des Umsatzes \(0.26\) Millionen GE/Jahr. □

3.3.3 Lokale Linearisierung

Wir werden sehen, dass uns die Ableitung erlaubt, eine nichtlineare Funktion lokal (dh. auf einem kleinen Intervall) durch eine lineare Funktion anzunähern und zu ersetzen. Wenn wir eine nichtlineare Funktion lokal durch eine lineare Funktion ersetzen, dann sprechen wir von lokaler Linearisierung. Eine solche lokale Linearisierung hat den Vorteil, dass manche Berechnungen einfacher werden, weil wir mit linearen Funktionen einfacher rechnen können als mit nichtlinearen Funktionen.

Geometrische Erklärung

Wir wollen nun eine geometrisch-anschauliche Erklärung für das Prinzip der lokalen Linearisierung geben. Diese anschauliche Erklärung wird durch die Abbildung 3.9 unterstützt.

Abbildung 3.9: Lokale Linearisierung.

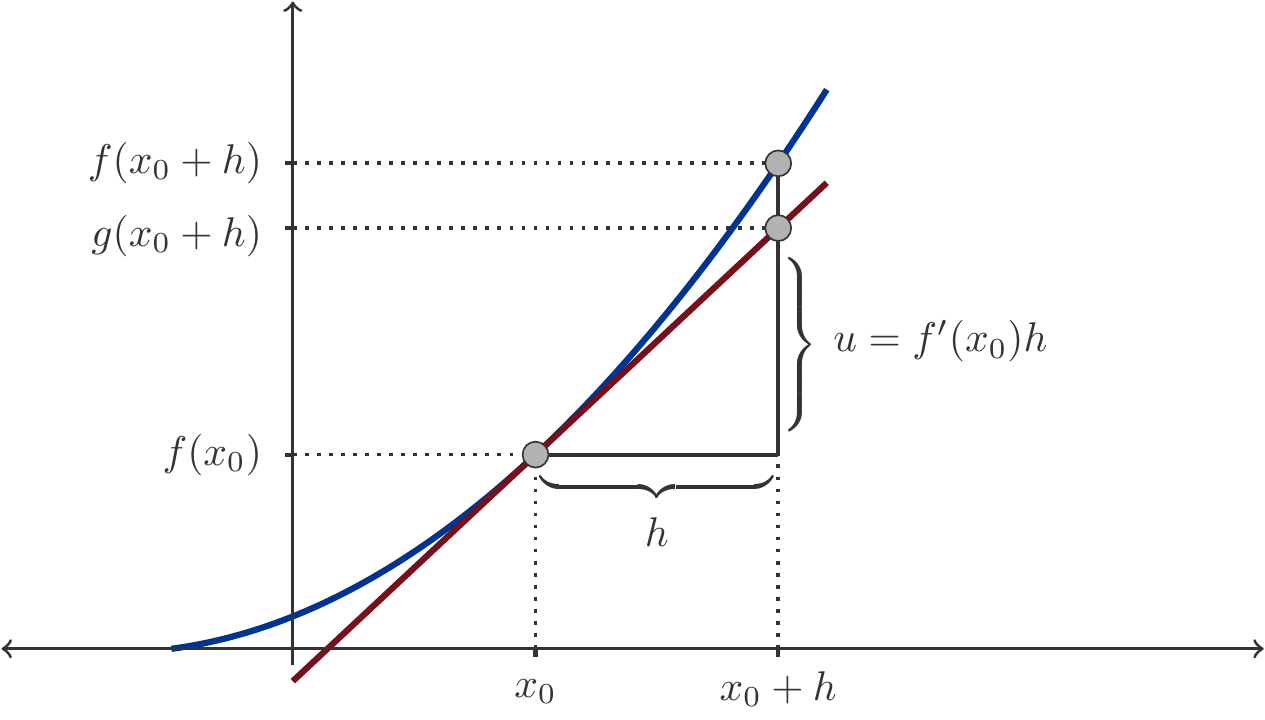
Zu Beginn erläutern wir die in der Abbildung 3.9 angedeutete Gleichung \(u=f'(x_0)h\).

Da die Tangente \(g\) eine Gerade ist, hat sie eine konstante Steigung. Wenn wir die Steigung auf dem Intervall \([x_0,x_0+h]\) ablesen, dann erhalten wir den Wert \(\frac{u}{h}\). Andererseits ist die Steigung der Tangente gleich \(f'(x_0)\) und daraus folgt daher \[ \begin{gathered} \frac{u}{h}=f'(x_0)\quad\mbox{bzw.}\quad u=f'(x_0)h. \end{gathered} \] Unser nächstes Ziel ist nun, ausgehend von \(f(x_0)\) den Funktionswert \(f(x_0+h)\) näherungsweise auszurechnen. Zu diesem Zweck bewegen wir uns entlang der Tangente \(g\) zum Punkt \((x_0+h,g(x_0+h))\). Der Funktionswert \(g(x_0+h)\) der Tangente beträgt einfach \[ \begin{gathered} g(x_0+h)=f(x_0)+u=f(x_0)+f'(x_0)h. \end{gathered} \] Da wir vorausgesetzt haben, dass der Abstand \(h\) klein ist, befinden wir uns an der Stelle \(x_0+h\) aber in der Nähe von \(x_0\), und daher können wir den Unterschied zwischen \(g(x_0+h)\) und \(f(x_0+h)\) vernachlässigen: Er ist wesentlich kleiner als der Abstand \(h\). Wir können daher sagen \[ \begin{gathered} f(x_0+h) \approx f(x_0)+f'(x_0)h. \end{gathered} \tag{3.28}\] Dies ist die einfachste mathematische Formulierung des Prinzips der lokalen Linearisierung.

Eine Tangente an den Funktionsgraphen ist selbst ein Funktionsgraph, und zwar der Graph einer ganz bestimmten linearen Funktion. Diese Funktion lautet \[ \begin{gathered} g(x)=f'(x_0)(x-x_0)+f(x_0). \end{gathered} \tag{3.29}\] Unter allen möglichen linearen Funktionen \(h(x)=ax+b\) ist die Funktion \(g\) durch zwei Eigenschaften besonders ausgezeichnet:

1. Es gilt \(g(x_0)=f(x_0)\), dh. \(g\) besitzt an der Stelle \(x_0\) den gleichen Funktionswert wie \(f\).

2. Es gilt \(g'(x_0)=f'(x_0)\), dh. \(g\) besitzt an der Stelle \(x_0\) die gleiche Ableitung wie \(f\).

Das Prinzip der lokalen Linearisierung lässt sich nun wie folgt zusammenfassen:

Satz 3.38 (Lokale Linearisierung) Ist eine Funktion \(f(x)\) in einem Punkt \(x_0\) differenzierbar, dann kann man sie lokal (in der Nähe von \(x_0\)) durch die lineare Funktion (3.29) approximieren.

Es ist für das Weitere sehr wichtig, das Prinzip der lokalen Linearisierung gut zu verstehen. Daher werden wir es im folgenden von mehreren verschiedenen Seiten beleuchten.

3.3.4 Marginale Änderung

Im Sprachgebrauch der Wirtschaftswissenschaften werden Ableitungen von ökonomischen Funktionen gerne als Grenzbegriffe bezeichnet. Die Ableitung einer Kostenfunktion nennt man Grenzkosten, die Ableitung einer Erlösfunktion nennt man Grenzerlös, usw. Bei der Interpretation dieser Grenzbegriffe wird häufig auf die entsprechenden marginalen Begriffe verwiesen.

Dieser Zusammenhang zwischen Grenzbegriffen soll im folgenden nun genauer erklärt werden.

Die marginalen Kosten sind die zusätzlichen Kosten, die bei der Mehrproduktion einer Mengeneinheit entstehen; der marginale Erlös ist der zusätzliche Erlös, der bei einer Preiserhöhung um eine GE entsteht. Allgemein versteht man unter der marginalen Änderung einer Funktion \(f\) an der Stelle \(x\) die Änderung \(f(x+1)-f(x)\), die entsteht, wenn man die Variable um eine Einheit erhöht.

Die Identifikation von Grenzbegriff und dem entsprechenden marginalen Begriff beruht auf der Möglichkeit der lokalen Linearisierung.

Wenn in der Gleichung (3.28) der Unterschied zwischen \(x\) und \(x_0\) genau 1 beträgt, dann ergibt sich für eine in \(x_0\) differenzierbare Funktion \[ \begin{gathered} f(x)-f(x_0)\approx f'(x_0). \end{gathered} \tag{3.30}\] Diese Approximation ist aber nur dann brauchbar, wenn auf der Skala, mit der die Variable \(x\) gemessen wird, die Differenz 1 eine kleine Änderung darstellt.

Kostenfunktionen

Es sei \(C(x)\) die Kostenfunktion eines Produktionsunternehmens. Wir nehmen an, dass die Kostenfunktion nichtlinear ist. Später in diesem Kapitel werden wir solche Beispiele für nichtlineare Kostenfunktionen kennenlernen.

Unter den marginalen Stückkosten versteht man die Kosten, die durch die Mehrproduktion einer Mengeneinheit verursacht werden. Ist \(x_0\) die im Moment produzierte Menge, dann betragen die marginalen Stückkosten \[ \begin{gathered} C(x_0+1)-C(x_0). \end{gathered} \] Das ist die Differenz der Funktionswerte der Kostenfunktion zwischen den Stellen \(x=x_0+1\) und \(x_0\). In der Regel ist die produzierte Menge \(x_0>0\) eine große Zahl, im Vergleich zu der eine einzige Mengeneinheit eine sehr kleine Änderung darstellt. Wenn die Kostenfunktion differenzierbar ist, können wir daher die marginalen Stückkosten mit lokaler Linearisierung approximieren: \[ \begin{gathered} C(x_0+1)-C(x_0)\approx C'(x_0)(x_0+1-x_0)=C'(x_0). \end{gathered} \tag{3.31}\] Da der Unterschied zwischen \(x=x_0+1\) und \(x_0\) genau 1 beträgt, erhalten wir gerade die Ableitung als Näherungswert für die marginalen Stückkosten. Man bezeichnet in der wirtschaftswissenschaftlichen Sprechweise die Ableitung der Kostenfunktion als Grenzkosten. Die Gleichung (3.31) erlaubt es, die Grenzkosten und die marginalen Stückkosten annähernd gleichzusetzen.

Musteraufgabe 3.39 Eine Kostenfunktion lautet \(C(x)=0.03x^2-0.9x+650\). Wie hoch sind die Grenzkosten und die Durchschnittskosten (Kosten pro Mengeneinheit) bei einem Produktionsniveau von \(x=1000\)?

Lösung: Die Ableitung der Kostenfunktion lautet \[ \begin{gathered} C'(x)=0.06x-0.9. \end{gathered} \] Die Grenzkosten für \(x=1000\) betragen daher \(C'(1000)=59.1\) GE/Mengeneinheit. Die Durchschnittskosten lauten \[ \begin{gathered} \overline{C}(x)=\frac{C(x)}{x}=0.03x-0.9+\frac{650}{x}. \end{gathered} \] Die Durchschnittskosten für \(x=1000\) betragen also \(\overline{C}(1000)=29.75\) GE/Mengeneinheit. □

3.3.5 Relative Änderungsrate

Wir wenden nun den Begriff der relativen Differenz auf die Analyse von Funktionen an. Wenn wir die Änderung der Funktionswerte auf einem Intervall messen wollen, dann haben wir bisher immer die Differenz der Funktionswerte an den Endpunkten des Intervalls als Maßzahl verwendet. Man kann an Stelle der Differenz der Funktionswerte auch die relative Änderung der Funktionswerte als Maßzahl verwenden. Dies ist vor allem dann wichtig, wenn die Werte der Funktion \(f(x)\) als eine Größe interpretiert werden, deren Unterschiede sinnvollerweise durch relative Differenzen gemessen werden sollten.

Definition 3.40 Es sei \(f(x)>0\) eine reelle Funktion und \([x_1,x_2]\) ein Intervall, das ganz im Definitionsbereich von \(f\) enthalten ist. Unter der relativen oder prozentuellen Änderung von \(f\) auf dem Intervall \([x_1,x_2]\) versteht man \[ \begin{gathered} r=\frac{f(x_2)-f(x_1)}{f(x_1)}=\frac{f(x_2)}{f(x_1)}-1. \end{gathered} \tag{3.32}\]

Es handelt sich bei der relativen Änderung um den Prozentsatz, um den sich \(f(x)\) ändert, wenn sich \(x\) vom Wert \(x_1\) auf den Wert \(x_2\) verschiebt. Ist die relative Änderung \(r\) gegeben, so ist \[ \begin{gathered} f(x_2)=f(x_1)+rf(x_1)=(1+r)f(x_1). \end{gathered} \tag{3.33}\]

Es sei nun \(y=f(x)\) eine differenzierbare Funktion. Wie wir im Abschnitt 3.1.1 gesehen haben, besteht die praktische Bedeutung der Ableitung einer Funktion \(f(x)\) darin, dass mit ihrer Hilfe kleine Änderungen von \(x\) in die entsprechenden Änderungen von \(f(x)\) umgerechnet werden können. Mit welcher Maßzahl können wir aber kleine Änderungen von \(x\) in die entsprechenden relativen (prozentuellen) Änderungen von \(f(x)\) umrechnen?

Wir nehmen die Antwort vorweg und geben anschließend die Erklärung dafür.

Definition 3.41 Es sei \(f(x)>0\) eine differenzierbare Funktion auf einem Intervall und \(x_0\) sei ein innerer Punkt des Intervalls. Dann heißt die Größe \[ \begin{gathered} c:=\frac{f'(x_0)}{f(x_0)}=\left(\ln f(x)\right)'\Big|_{x=x_0} \end{gathered} \tag{3.34}\] die (momentane) relative Änderungsrate der Funktion \(f(x)\) an der Stelle \(x_0\).

Mit anderen Worten: \(c\) ist die logarithmische Ableitung von \(f(x)\) an der Stelle \(x_0\), die wir schon in der Formel (3.24) kennengelernt haben.

Nun wollen wir erklären, warum die relative Änderungsrate das zu Beginn formulierte Problem löst. Durch lokale Linearisierung erhalten wir \[ \begin{gathered} f(x)\approx f(x_0)+f'(x_0)(x-x_0), \end{gathered} \] und daraus folgt \[ \begin{gathered} \frac{f(x)-f(x_0)}{f(x_0)}\approx \frac{f'(x_0)}{f(x_0)}(x-x_0). \end{gathered} \] Setzt man \(x:=x_0+h\), so erhält man \[ \begin{gathered} \frac{f(x_0+h)-f(x_0)}{f(x_0)}\approx \frac{f'(x_0)}{f(x_0)}h. \end{gathered} \tag{3.35}\] Das heißt, die relative Änderungsrate ist genau jener Faktor \(c\), mit dem wir kleine Änderungen \(h=x-x_0\) der \(x\)-Werte multiplizieren müssen, um die relative Änderung der Funktionswerte zu erhalten, also \[ \begin{gathered} \mbox{$\displaystyle \frac{f(x_0+h)-f(x_0)}{f(x_0)}\approx c\cdot h \quad\mbox{und}\quad f(x_0+h)\approx (1+ch)f(x_0)$}. \end{gathered} \tag{3.36}\]

Wir fassen nochmals zusammen:

Die relative Änderungsrate \(c=\dfrac{f'(x)}{f(x)}\) gibt den Faktor an, mit dem man (kleine) absolute Änderungen von \(x\) in die entsprechenden relativen (prozentuellen) Änderungen von \(f\) umrechnen kann.

Bemerkung 3.42 (Ableitung und relative Änderungsrate) Wir haben nun zwei Größen zu Verfügung, die uns sagen, wie stark sich eine Funktion \(y=f(x)\) verändert, wenn man die Variable \(x\) geringfügig verändert. Die erste Größe ist die Ableitung oder die momentane Änderungsrate. Sie sagt uns, wie stark sich der Funktionswert verändert, wenn wir den Funktionswert in der ursprünglichen Maßeinheit messen. Die zweite Größe ist die (momentane) relative Änderungsrate. Sie sagt uns, wie stark sich der Funktionswert relativ (prozentuell) zum Ausgangswert ändert. Die relative Änderungsrate ist die richtige Maßzahl für die momentane Änderung einer Funktion \(y=f(x)\), wenn wir Unterschiede der Variablen \(x\) durch Differenzen beschreiben, aber Unterschiede der Funktionswerte durch relative Differenzen.

Musteraufgabe 3.43 Was ist die relative Wachstumsrate von \(f(x)=2e^{-3x^2}\). Welchen Wert hat sie an der Stelle \(x_0=1\)?

Lösung: Die relative Wachstumsrate ist die logarithmische Ableitung von \(f(x)\). Daher bilden wir zuerst \(\ln f(x)\). Mit den Rechenregeln für Logarithmen, die wir in 2.34 und 2.35 formuliert haben, erhalten wir: \[ \begin{gathered} \ln f(x)=\ln(2e^{-3x^2})= \ln 2-3x^2. \end{gathered} \] Damit finden wir: \[ \begin{gathered} \left(\ln f(x)\right)'=\left(\ln 2-3x^2\right)'=-6x. \end{gathered} \] An der Stelle \(x_0=1\) ist \(c=-6\). □

Musteraufgabe 3.44 Das BIP eines Landes wächst nach der Formel \(f(t)=1200t^{1.2}\). Wie hoch ist die prozentuelle Wachstumsgeschwindigkeit zum Zeitpunkt \(t=20\)?

Lösung: Die relative Wachstumsrate ergibt sich als logarithmische Ableitung im Punkt \(t=20\). Zunächst bilden wir: \[ \begin{gathered} \ln f(t)=\ln\left(1200t^{1.2}\right)=\ln 1200 + 1.2\ln t. \end{gathered} \] Das ergibt: \[ \begin{gathered} \frac{f'(x)}{f(x)}=\left(\ln 1200 +1.2\ln t\right)'=\frac{1.2}{t}\,. \end{gathered} \] Zum Zeitpunkt \(t=20\) beträgt sie daher \(0.06\), das ist eine Wachstumsgeschwindigkeit von 6 Prozent pro Zeiteinheit. □

3.3.6 Exponentielles Wachstum

Bei linearen Funktionen ist die Ableitung konstant und das ist gewissermaßen die kennzeichnende Eigenschaft von linearen Funktionen. Es gibt keine anderen Funktionen, bei denen die Ableitung konstant ist. Dagegen ist die relative Änderungsrate von linearen Funktionen nicht konstant.

Es gibt aber auch Funktionen, bei denen die relative Änderungsrate konstant ist.

Satz 3.45 Es sei \(f(x)=Aa^x\) eine Exponentialfunktion. Die relative Änderungsrate dieser Funktion beträgt \[ \begin{gathered} \frac{f'(x)}{f(x)}=\ln a \quad\mbox{für alle $x\in\mathbb R$}. \end{gathered} \]

Begründung: Man kann das leicht nachrechnen. Wir wissen ja, dass \[ \begin{gathered} \frac{f'(x)}{f(x)}=\left(\ln(Aa^x)\right)'=\left(\ln A+x\ln a\right)'=\ln a. \end{gathered} \] □

Das Bemerkenswerte an Exponentialfunktionen ist also, dass ihre relative Änderungsrate konstant ist. Die Exponentialfunktionen sind also eine ebenso wichtige Klasse von Funktionen wie die linearen Funktionen. Bei den linearen Funktionen ist die Ableitung konstant, bei den Exponentialfunktionen ist es die relative Änderungsrate, die unveränderlich ist.

Wie wir aus (2.37) wissen, lässt sich jede Exponentialfunktion mit einer beliebigen Basis \(a>0\) durch die Exponentialfunktion \(\exp(x)=e^x\) darstellen. Es ist \[ \begin{gathered} f(x)=Aa^x=Ae^{x\ln a}=Ae^{cx}\quad \mbox{mit $c:=\ln a$}. \end{gathered} \tag{3.37}\] Hier taucht der natürliche Logarithmus \(\ln a\) wieder auf, den wir ursprünglich im Satz 2.58 schon an dieser Stelle bemerkt haben, aber damals noch nicht interpretieren konnten (es sei denn als nominellen Zinssatz bei kontinuierlicher Verzinsung, vgl. Abschnitt 2.6.2. Jetzt wissen wir, dass es sich dabei einfach um die relative Änderungsrate handelt. Wir können also eine Funktion der Form \[ \begin{gathered} f(x)=Ae^{cx} \end{gathered} \tag{3.38}\] ganz einfach in Worten beschreiben: Der Anfangswert ist \(f(0)=A\) und die relative Änderungsrate ist konstant und beträgt \(c\). Damit ist alles über die Funktion \(f\) gesagt.

Beispiel 3.46 (Bevölkerungswachstum)

Nehmen wir an, dass die relative Wachstumrate einer Bevölkerung konstant gleich \(c=0.17\) ist, dh. dass die Bevölkerung in gleichen Zeitintervallen stets um den gleichen Prozentsatz wächst. Dann können wir die veränderliche Bevölkerungszahl durch eine Exponentialfunktion mit der relativen Änderungsrate \(c=0.17\) beschreiben. Es muss also gelten \[ \begin{gathered} f(t)=Ae^{0.17t}. \end{gathered} \] Damit haben wir ein exaktes mathematisches Modell für die zeitliche Entwicklung gewonnen und brauchen die relative Änderung zwischen zwei Zeitpunkten nicht mehr durch numerische Näherungen zu schätzen, wie wir das früher gemacht haben. Die relative Änderung zwischen zwei Zeitpunkten \(t_0\) und \(t\) beträgt jetzt \[ \begin{gathered} r=\frac{f(t)-f(t_0)}{f(t_0)}=\frac{Ae^{0.17t}-Ae^{0.17t_0}}{Ae^{0.17t_0}} =e^{0.17(t-t_0)}-1. \end{gathered} \] Angenommen, die Bevölkerung hat zur Zeit \(t_0\) eine Größe von \(f(t_0)=1\) Mio. Verstreicht ein Monat, dann ist \(t-t_0=\frac{1}{12}\) und \[ \begin{gathered} r=e^{0.17/12}-1=0.014267\,. \end{gathered} \] Daher ist nach (3.33): \[ \begin{gathered} f\Big(t_0+\frac{1}{12}\Big)=(1+r)f(t_0)=1\,014\,267. \end{gathered} \] Verstreicht ein halbes Jahr, dann ist \[ \begin{gathered} r=e^{0.17/2}-1=0.088717 \end{gathered} \] und daher ist \[ \begin{gathered} f\Big(t_0+\frac{1}{2}\Big)=(1+r)f(t_0)=1\,088\,717. \end{gathered} \]

Musteraufgabe 3.47 Das Bruttoinlandsprodukt (BIP) Österreichs stieg zwischen \(2000\) und \(2010\) von \(214\) Mrd auf \(296\) Mrd Euro. Angenommen, die relative Wachstumsrate war konstant.

1. Wie hoch ist die relative Wachstumsrate?

2. Wann erreicht das BIP die Höhe von \(370\) Mrd. Euro?

Lösung:

(a) Da die relative Wachstumsrate als konstant vorausgesetzt wird, können wir als mathematisches Modell das einer Exponentialfunktion annehmen: \[ \begin{gathered} f(t) = A\cdot(1+r)^{t} = A\cdot a^{t} = A\cdot e^{ct}. \end{gathered} \] Den Anfangszeitpunkt \(2000\) identifizieren wir mit \(t=0\), der Anfangszustand beträgt daher \(A =f(0)= 214\), und das Jahr \(2010\) entspricht \(t = 10\). Unser Modellansatz führt so auf eine Potenzgleichung, die wir lösen können: \[ \begin{aligned} f(t)&=A\cdot a^{t}, \\ f(10)&= 214\cdot a^{10} = 296, \\ a^{10}& = \dfrac{296}{214}, \\ a& = \left(\dfrac{296}{214}\right)^{1/10} = 1.032970, \\ c &= \ln\,1.032970 = 0.032438\,.\end{aligned} \] Der jährliche Zuwachs beträgt \(r=a-1\simeq 0.033\), also ca. 3.3%, die relative Wachstumsrate ist \(c\simeq 0.032\), das sind 3.2%.

(b) Wir rechnen mit \(a=1.033\). Die Fragestellung führt auf eine Exponentialgleichung: \[ \begin{gathered} f(t) =A\cdot a^{t} = 214\cdot1.033^{t} = 370, \\[5pt] 1.033^{t} = \dfrac{370}{214} \quad\implies\quad t = 16.864\simeq 17. \end{gathered} \] Das Jahr, in dem die Höhe von \(370\) Mrd. erreicht wird, ist also \(2000 + 17 = 2017\). Tatsächlich betrug das BIP Österreichs im Jahr 2017 370.16 Mrd. Euro. □

Musteraufgabe 3.48 Die Bevölkerung eines Entwicklungslandes wächst jährlich um \(3\)%. Wie stark muss das BIP jährlich wachsen, damit sich das Einkommen pro Kopf innerhalb von \(20\) Jahren verdoppelt?

Lösung: Die Bevölkerung wächst nach dem Modell einer Exponentialfunktion \(B(t) = B(0)\cdot1.03^{t}\). Für das BIP unterstellen wir das gleiche Modell mit einer unbekannten Wachstumsrate: \(E(t) = E(0)\cdot a^{t}\).

Das Einkommen pro Kopf ergibt sich daraus als Quotient: \[ \begin{gathered} \dfrac{E(t)}{B(t)} = \dfrac{E(0)}{B(0)}\cdot\bigg(\dfrac{a}{1.03}\bigg)^{t}. \end{gathered} \] Dieses Einkommen pro Kopf soll innerhalb von 20 Jahren verdoppelt werden: \[ \begin{gathered} \dfrac{E(0)}{B(0)}\cdot\bigg(\dfrac{a}{1.03}\bigg)^{20} = 2\cdot \dfrac{E(0)}{B(0)} \quad \Rightarrow \quad \bigg(\dfrac{a}{1.03}\bigg)^{20} = 2. \end{gathered} \] Diese Exponentialgleichung hat die Lösung \[ \begin{gathered} a = 1.03\cdot\sqrt[20]{2} = 1.066323 \; \Rightarrow\; \mbox{Jährliche Wachstumsrate $6.6\%$}, \end{gathered} \] bzw. \[ \begin{gathered} c = \ln\,a = 0.0642 \; \Rightarrow\; \mbox{Relative Wachstumsrate $6.4\%$}\,. \end{gathered} \] □

3.3.7 Elastizitäten

Wir kennen jetzt zwei Maßzahlen, mit denen wir die Änderungen einer Funktion ausdrücken können, nämlich die Ableitung und die relative Änderungsrate. Es gibt aber noch eine dritte Maßzahl, die für wirtschaftliche Anwendungen fast noch wichtiger ist als die ersten beiden.

Es sei \([x_1,x_2]\) ein Intervall in der Definitionsmenge der Funktion \(y=f(x)\). Wir setzen dabei voraus, dass \(0<x_1<x_2\) und \(f(x)>0\) auf dem ganzen Intervall \([x_1,x_2]\). Wenn wir die relative Änderung der Funktionswerte \(f(x)\) der relativen Änderung der Variablen \(x\) gegenüberstellen wollen, dann bilden wir die Verhältniszahl \[ \begin{gathered} \frac{f(x_2)-f(x_1)}{f(x_1)}:\frac{x_2-x_1}{x_1}= \frac{f(x_2)-f(x_1)}{x_2-x_1}\frac{x_1}{f(x_1)}. \end{gathered} \tag{3.39}\] Wenn die Funktion differenzierbar und wenn das Intervall sehr klein ist, dann können wir den Differenzenquotienten (also die Steigung der Sekante) durch die Ableitung ersetzen (das ist die Steigung der Tangente) und erhalten so die Maßzahl \[ \begin{gathered} \epsilon(x_1):=f'(x_1)\frac{x_1}{f(x_1)}=\frac{f'(x_1)}{f(x_1)}x_1. \end{gathered} \tag{3.40}\] Die Größe (3.39) ist also gleichsam ein Näherungswert für die Größe in (3.40).

Die Größe \(\epsilon(x)\) spielt auch in den Naturwissenschaften eine Rolle und daher bezieht sie ihren Namen.

Definition 3.49 (Elastizität) Es sei \(y=f(x)>0\) eine differenzierbare Funktion auf \((0,\infty)\) und es sei \(x_0>0\). Dann heißt die Größe \[ \begin{gathered} \epsilon(x_0):=\frac{f'(x_0)}{f(x_0)}x_0=\left(\ln f(x)\right)' x \Big|_{x=x_0} \end{gathered} \tag{3.41}\] die Elastizität von \(f\) an der Stelle \(x_0\).

Interpretation

Zunächst halten wir fest, dass sich die Elastizität einer Funktion wieder mit Hilfe der logarithmischen Ableitung berechnen lässt, wie (3.41) zeigt.

Elastizitäten spielten in den Wirtschaftswissenschaften als Reagibilitätsmaße eine sehr wichtige Rolle. Wir sehen uns daher noch einen zweiten Weg an, auf dem wir die Elastizität erklären können.

Wie kann man eine kleine relative Änderung von \(x\) in die entsprechende relative Änderung von \(f(x)\) umrechnen? Wir wenden die Methode der lokalen Linearisierung an. Es werde \(x_0\) um einen kleinen Prozentsatz \(h\) erhöht: \[ \begin{gathered} \frac{x-x_0}{x_0}=h \implies x=x_0+hx_0. \end{gathered} \] Die Größe \(h\) ist also die relative Änderung von \(x\). Dann folgt durch lokale Approximation mit einer linearen Funktion \[ \begin{gathered} f(x_0+hx_0)\approx f(x_0)+f'(x_0)hx_0, \end{gathered} \] und daher \[ \begin{gathered} \frac{f(x_0+hx_0)-f(x_0)}{f(x_0)} \approx \frac{f'(x_0)}{f(x_0)}x_0\cdot h= \epsilon(x_0)\cdot h. \end{gathered} \tag{3.42}\] Ist z.B. \(h=0.01\), wird also \(x_0\) um 1 Prozent erhöht, dann ist \[ \begin{gathered} \frac{f(x_0+0.01\,x_0)-f(x_0)}{f(x_0)} \approx \epsilon(x_0)\cdot 0.01. \end{gathered} \tag{3.43}\] Das heißt: Wenn \(x_0\) um 1 Prozent erhöht wird, dann beträgt die relative Änderung \(\epsilon(x_0)\) Prozent.

Dies halten wir in der folgenden Übersicht fest:

Interpretation der Elastizität

Die Elastizität einer Funktion \(f\) gibt den Faktor an, mit dem man eine relative Änderung von \(x\) in die entsprechende relative Änderung von \(f(x)\) umrechnen kann.

Beispiel 3.50 (Preiselastizität der Nachfrage)

Es sei \(q(p)\) die nachgefragte Menge \(q\) ein Produkts in Abhängigkeit vom Preis \(p\). In der Regel ist \(q(p)\) eine fallende Funktion des Preises, d.h. \(q'(p)<0\) für \(p>0\).

Die Preiselastizität der Nachfrage \[ \begin{gathered} \epsilon(p)=\frac{q'(p)}{q(p)}p \end{gathered} \] ist ein Maß für die Reaktion der Nachfrage auf kleine prozentuelle Änderungen des Preises: Um wieviel Prozent sinkt die Nachfrage bei (kleiner) prozentueller Änderung des Preises?

Da \(q'(p)<0\) ist auch \(\epsilon(p)<0\) für \(p> 0\). Ist \(-1< \epsilon(p)\le 0\), so sagt man auch, die Nachfrage reagiere unelastisch auf Preisänderungen, weil Preisänderungen zu unterproportionalen Nachfragereduktionen führen. Ist hingegen \(-\infty<\epsilon(p)\le -1\), dann nennt man die Nachfrage elastisch. Konsumenten reagieren markant auf Preiserhöhungen.

Musteraufgabe 3.51 Die Nachfrage sei linear im Preis mit \(q(p)=-0.25p+50\). Welchen Wert hat die Preiselastizität der Nachfrage bei Preisen \(p=50, 100, 180\)?

Lösung: Mit Hilfe von (3.41): \[ \begin{gathered} \epsilon(p)=\frac{-0.25p}{-0.25p+50}=-\frac{p}{200-p}. \end{gathered} \] Dies ergibt \[ \begin{gathered} \epsilon(50)=-\frac{1}{3}\simeq -0.33,\quad \epsilon(100)=-1,\quad \epsilon(180)=-9. \end{gathered} \] Wäre der Preis 180 GE und würde um 1 % auf 181.8 GE erhöht, dann sinkt die Nachfrage um 9 %. □

Musteraufgabe 3.52 Man berechne die Elastizität von \(f\) bezüglich \(x\) an der Stelle \(x_0\), wobei \(f(x) = e^{-10\sqrt{x}}\) und \(x_0=1\).

Lösung: Wir berechnen die Elastizität aus der logarithmischen Ableitung von \(f(x)\): \[ \begin{aligned} \ln f(x) &= \ln\left(e^{-10\sqrt{x}}\right)= - 10\sqrt{x}\\[5pt] \left(\ln f(x)\right)'&= \left(-10\sqrt{x}\right)'=-\frac{10}{2\sqrt{x}}=-\frac{5}{\sqrt{x}} \end{aligned} \] Aus (3.41) folgt: \[ \begin{gathered} \epsilon(x)=\left(\ln f(x)\right)'x=-5\sqrt{x}\quad\text{und}\quad \epsilon(1)=-5. \end{gathered} \] Interpretation, falls \(f(x)\) eine Nachfragefunktion ist: Wenn der Preis ausgehend von \(x=1\) GE um \(1\%\) steigt, dann sinkt die Nachfrage um \(5\%\). □

Musteraufgabe 3.53 Die Betriebskosten \(B\) einer Wohnung hängen von den Ausgaben für die Miete \(M\) auf folgende Weise ab: \[ \begin{gathered} B=5\sqrt{1+1.5M}. \end{gathered} \] Berechnen Sie die Elastizität der Betriebskosten \(B\) bezüglich der Mietausgaben \(M\), wenn diese 500 GE betragen.

Lösung: Die Rechnung verläuft so: \[ \begin{aligned} \ln B&=\ln\left(5\sqrt{1+1.5M}\right)=\ln 5+\frac{1}{2}\ln(1+1.5M),\\ (\ln B)'&= \frac{1.5}{2(1+1.5M)},\\ \epsilon(M)&=(\ln B)'M=\frac{0.75M}{1+1.5M}\,.\end{aligned} \] An der Stelle \(M=500\) finden wir den Wert: \[ \begin{gathered} \varepsilon(500)=\frac{0.75\cdot 500}{1+1.5\cdot 500} =0.49933 \end{gathered} \] Dass \(\epsilon(500)\) so nahe bei \(1/2\) liegt, ist keineswegs ein Zufall. □

Konstante Elastizität

Es ist uns jetzt klar, dass die Elastizität eine interessante Größe ist. Nun ist es naheliegend zu fragen: gibt es Funktionen deren Elastizität konstant ist? Für die verwandten Größen, nämlich für die Ableitung und für die relative Änderungsrate, kennen wir die entsprechende Antwort schon.

Satz 3.54 (Konstante Elastizität) Es sei \(f\) eine Potenzfunkion, also \(f(x)=Ax^c\) für \(x>0\). Dann beträgt die Elastizität dieser Funktion \(\epsilon(x)=c\) für alle \(x>0\).

Begründung: Wir rechnen nach: \[ \begin{gathered} \ln f(x)=\ln\left(Ax^c\right)=\ln A+c\ln x\implies (\ln f(x))'=\frac{c}{x} \end{gathered} \] Daher ist \(\epsilon(x)=\dfrac{c}{x}\cdot x=c\). □

Musteraufgabe 3.55 Die optimale Bestellmenge \(x\) eines Unternehmens hänge vom Lagerkostensatz \(h\) (GE pro Stück und Zeiteinheit) auf folgende Weise ab: \[ \begin{gathered} x(h)=\sqrt{\frac{a}{h}}. \end{gathered} \] Zu berechnen ist die Elastizität der Bestellmenge bezüglich des Lagerkostensatzes.

Lösung: Die Bestellmenge \(x(h)\) lässt sich so schreiben: \[ \begin{gathered} x(h)=\left(\frac{a}{h}\right)^{1/2}=a^{1/2}\cdot h^{-1/2}\implies \epsilon(h)=-\frac{1}{2}. \end{gathered} \]

3.4 Kurvendiskussion

3.4.1 Analyse der Monotonieeigenschaften

Die Grundlage für viele wichtige Schlussfolgerungen, die man aus den Eigenschaften der Ableitung ziehen kann, ist der sogenannte Mittelwertsatz der Differentialrechnung.

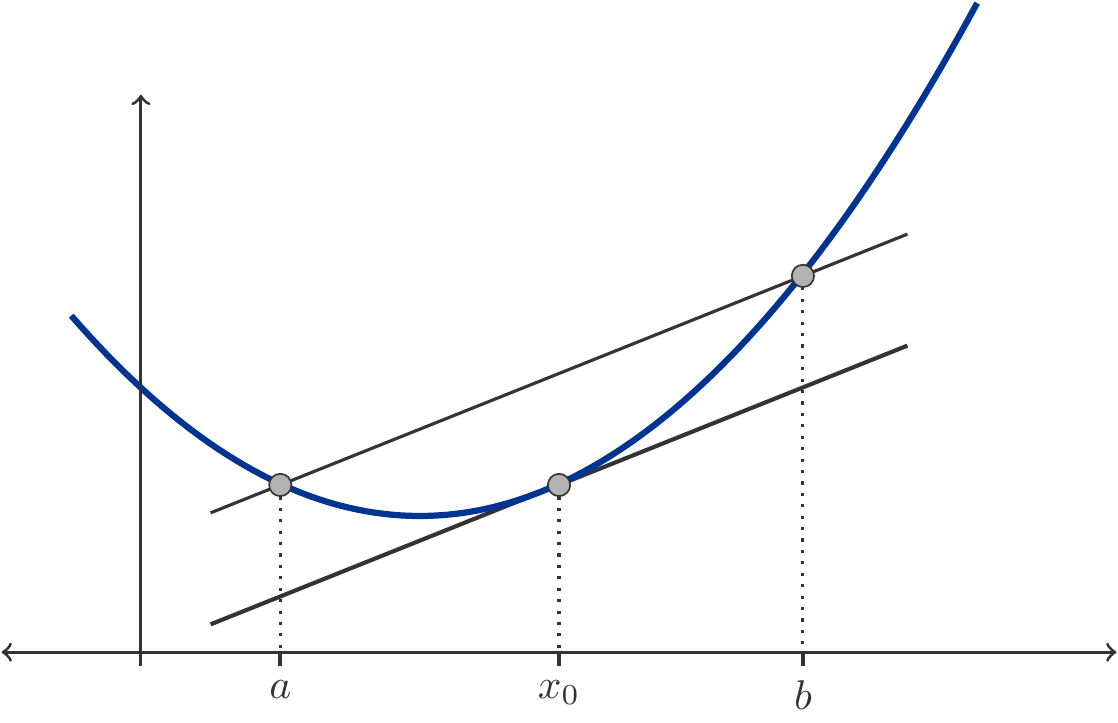
Satz 3.56 (Mittelwertsatz) Ist die Funktion \(f\) auf dem Intervall \([a,b]\) stetig und im Innern differenzierbar, dann gibt es mindestens einen Punkt \(x_0\) im Innern des Intervalls, sodass \[ \begin{gathered} f(b)-f(a)=f'(x_0)(b-a), \end{gathered} \tag{3.44}\] dh. dass die Ableitung genauso groß ist wie das Steigungsverhältnis der Funktion auf dem Intervall \([a,b]\).

Wir verzichten auf einen formal strengen Beweis des Mittelwertsatzes. Der Mittelwertsatz besitzt eine sehr einfache und anschauliche Deutung: Es gibt einen Punkt \(x_0\) im Inneren des Intervalls, an dem die Tangente parallel zur Verbindungsgeraden von \((a,f(a))\) und \((b,f(b))\) ist. Vgl. dazu Abbildung 3.10.

Abbildung 3.10: Zum Mittelwertsatz.

Erinnern wir uns nun an die Definition von monotonen Funktionen im Abschnitt 3.1.1. Da die geometrische Bedeutung der Ableitung die Steigung der Tangente ist, und weil die Steigung der Tangente anschaulich in engem Zusammenhang mit dem Monotonieverhalten der Funktion steht, liegt es nahe, aus dem Vorzeichen der Ableitung Schlüsse über das Monotonieverhalten der Funktion zu ziehen.

Wir haben das im Grunde schon oft getan, indem wir die Ableitung näherungsweise als marginale Änderung interpretiert haben. Der folgende Satz wiederholt diese Zusammenhänge.

Satz 3.57 Es sei \(f\) eine differenzierbare Funktion auf einem offenen Intervall \((a,b)\).

1. Wenn \(f'(x)>0\) für \(x\in (a,b)\), so ist \(f(x)\) auf \((a,b)\) streng monoton wachsend.

2. Wenn \(f'(x)<0\) für \(x\in (a,b)\), so ist \(f(x)\) auf \((a,b)\) streng monoton fallend.

Begründung: Es sei \(f'(x)>0\) für \(x\in (a,b)\). Sind \(x,y<b\) zwei beliebige Punkte in \((a,b)\) mit \(x<y\), so haben wir zu zeigen, dass \(f(x)<f(y)\).

Nach dem Mittelwertsatz gibt es einen Punkt \(x_0\) mit der Eigenschaft \[ \begin{gathered} f(y)-f(x)=f'(x_0)(y-x). \end{gathered} \] Da \(f'(x_0)>0\) und \(y-x>0\), folgt \(f(y)-f(x)>0\) und daher \(f(y)>f(x)\). □

Man kann also aus dem Vorzeichen der ersten Ableitung ablesen, ob die Funktion \(f\) wächst oder fällt.

Für ein Intervall \((a,b)\), das einen Punkt \(x\) mit der Eigenschaft \(f'(x)=0\) enthält, ist eine Aussage über die Monotonie nicht ohne weiteres möglich. An solchen Punkten hat der Funktionsgraph eine waagrechte Tangente.

Satz 3.58 (Kritische Punkte) Es sei \(f\) eine differenzierbare Funktion auf einem offenen Intervall \((a,b)\) und es sei \(x\in(a,b)\). Ist \(f'(x)=0\), so heißt \(x\) ein kritischer Punkt von \(f(x)\).

Die anschauliche Bedeutung von kritischen Punkten wird durch den folgenden Satz klar.

Satz 3.59 Es sei \(f\) eine differenzierbare Funktion auf einem offenen Intervall \((a,b)\). Zwischen zwei benachbarten kritischen Punkten von \(f\) in \((a,b)\) ändert die erste Ableitung ihr Vorzeichen nicht.

Begründung: Der Satzes beruht auf einer von uns nicht bewiesenen Zwischenwerteigenschaft von Ableitungen: Ist \(x_1<x_2\) und \(f'(x_1)\not=f'(x_2)\), so nimmt die Ableitung \(f'(x)\) auf dem Intervall \((x_1,x_2)\) alle Werte zwischen \(f'(x_1)\) und \(f'(x_2)\) an. Auch der Mittelwertsatz beruht im Grunde auf dieser Zwischenwerteigenschaft. Anschaulich ist die Zwischenwerteigenschaft der Ableitung plausibel: Eine Ableitung kann sich bei einer überall differenzierbaren Funktion nicht sprungartig ändern, denn würde sie das tun, entstünde eine Knickstelle und dort wäre die Funktion dann nicht differenzierbar.

Die Begründung für die Aussage des Satz 3.59 verläuft dann so: Würde sich das Vorzeichen der Ableitung zwischen zwei kritischen Punkten ändern, dann gibt es Punkte \(x\) und \(y\) mit \(f'(x)<0\) und \(f'(y)>0\). Folglich gibt es zwischen \(x\) und \(y\) einen Punkt \(x_0\), sodass \(f'(x_0)=0\). Das ist ein aber kritischer Punkt und folglich sind die beiden kritischen Punkte \(x\) und \(y\) dann nicht benachbart. □

Aus dem Satz 3.59 können wir schließen: Es seien \(x_1<x_2\) zwei kritische Punkte, zwischen denen kein weiterer kritischer Punkt liegt. Dann ist die Funktion \(f(x)\) auf dem Intervall \((x_1,x_2)\) entweder streng monoton wachsend oder streng monoton fallend. Oder in anderen Worten: Zwischen zwei aufeinander folgenden kritischen Punkten ändert sich das Monotonieverhalten einer Funktion nicht.

Wir nennen ein Intervall, in dem sich das Monotonieverhalten einer Funktion nicht ändert (wo die Funktion also entweder durchgehend streng monoton wachsend oder durchgehend streng monoton fallend ist), ein Monotonieintervall der Funktion. Für eine qualitative Beschreibung eines Funktionsgraphen ist die Kenntnis der Monotonieintervalle von Bedeutung.

Musteraufgabe 3.60 Bestimme die Monotonieintervalle der Funktion \(y=x^3-3x\).

Lösung: Die Ableitung der Funktion lautet \(f'(x)=3x^2-3\). Die kritischen Punkte mit \(f'(x)=0\) sind \(x_1=-1\) und \(x_2=1\). Die beiden kritischen Punkte teilen den Definitionsbereich in drei Intervalle ein: \((-\infty,-1)\), \((-1,1)\) und \((1,\infty)\). In jedem dieser Intervalle ist die Funktion streng monoton.

Um festzustellen, wo die Funktion steigt bzw. fällt, berechnen wir die Ableitung in jeweils einem (beliebigen) Punkt der drei Intervalle, z.B. in \(x=-2, x=0\) und \(x=2\). Wir finden: \(f'(-2)>0\), \(f'(0)<0\) und \(f'(2)>0\). Daher ist die Funktion auf dem Intervall \((-\infty,-1)\) streng monoton wachsend, auf dem Intervall \((-1,1)\) streng monoton fallend, und auf dem Intervall \((1,\infty)\) wieder streng monoton wachsend, siehe Abbildung 3.11. □

Abbildung 3.11: Die Funktion \(f(x)=x^3-3x\).

An einem kritischen Punkt kann sich die Richtung der Monotonie ändern, sie muss es aber nicht tun. Wenn sich an einem kritischen Punkt die Richtung der Monotonie ändert, so handelt es sich bei dem kritischen Punkt um einen relativen Extremwert.

Definition 3.61 (Relative Extremwerte) Ein kritischer Punkt \(x_0\) ist ein relatives Maximum, wenn an Punkten \(x\) in einem offenen Intervall um \(x_0\) \[ \begin{gathered} f'(x)=\left\{ \begin{array}{ll} >0 & x<x_0 \\ =0 & x=x_0 \\ <0 & x>x_0 \end{array} \right. \end{gathered} \tag{3.45}\] Der kritische Punkt \(x_0\) ist ein relatives Minimum, wenn an Punkten \(x\) in einem offenen Intervall um \(x_0\) \[ \begin{gathered} f'(x)=\left\{ \begin{array}{ll} <0 & x<x_0 \\ =0 & x=x_0 \\ >0 & x>x_0 \end{array} \right. \end{gathered} \tag{3.46}\]

Musteraufgabe 3.62 Bestimme die relativen Extremstellen der Funktion \(y=x^4-4x^3+7\).

Lösung: Die Ableitung lautet \[ \begin{gathered} f'(x)=4x^3-12x^2=4x^2(x-3). \end{gathered} \] Also gibt es zwei kritische Punkte \(x_1=0\) (eine doppelte Nullstelle von \(f'(x)\)) und \(x_2=3\). Da \(f'(-1)<0\), \(f'(1)<0\) und \(f'(4)>0\), ist die Funktion auf beiden Intervallen \((-\infty,0)\) und \((0,3)\) streng monoton fallend und auf dem Intervall \((3,\infty)\) streng monoton wachsend. Folglich ist der kritische Punkt \(x_2=3\) ein relatives Minimum, während der kritische Punkt \(x_1=0\) keine relative Extremstelle ist, siehe Abbildung 3.12.

Abbildung 3.12: Die Funktion \(f(x)=x^4-4x^3+7\).

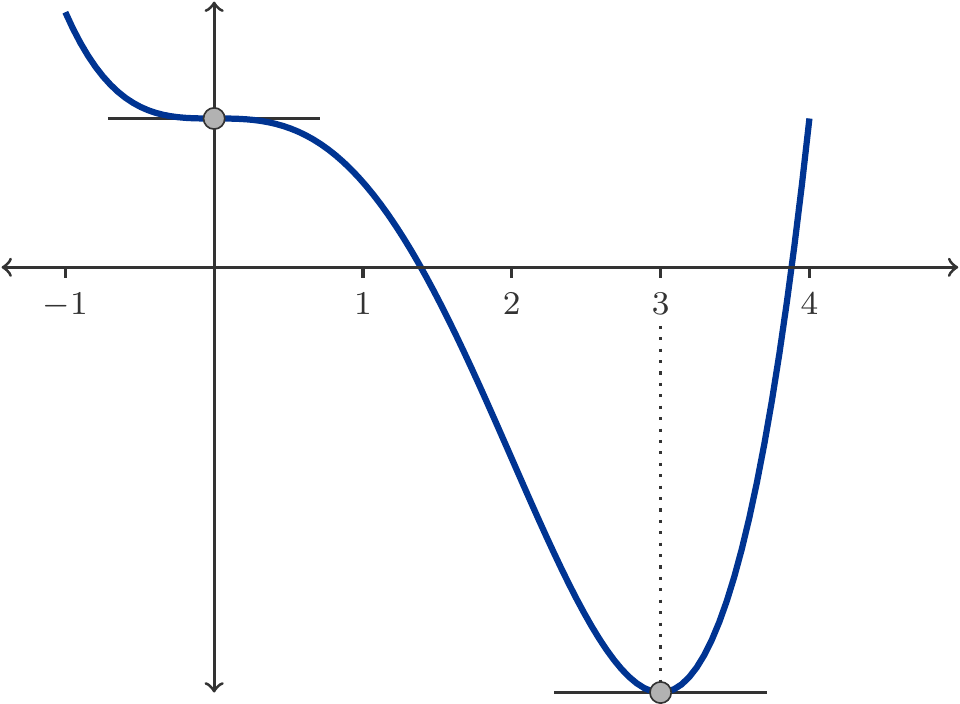
Die Funktion besitzt zwei maximale Monotonieintervalle: Auf dem ersten Monotonieintervall \((-\infty,3)\) ist die Funktion streng monoton fallend. Dieses Monotonieintervall enthält einen kritischen Punkt. Auf dem zweiten Monotonieintervall \((3,\infty)\) ist die Funktion streng monoton wachsend. □

Man darf ein relatives Maximum oder ein relatives Minimum nicht mit einem (absoluten) Maximum (größter Funktionswert) oder einem (absoluten) Minimum (kleinster Funktionswert) verwechseln. Es kann sein, dass eine Funktion gar kein Maximum oder Minimum besitzt. Wenn ein absolutes Maximum oder ein absolutes Minimum existiert, dann muss es sich dabei nicht um einen kritischen Punkt handeln. Man denke an eine streng monotone Funktion auf einem abgeschlossenen Intervall \([a,b]\): Maximum und Minimum liegen auf den Rändern des Definitionsintervalles. Nur wenn das Maximum oder Minimum einer differenzierbaren Funktion im Innern des Definitionsintervalles liegen, handelt es sich um auch um relative Extremstellen und damit um kritische Punkte.

Beispiel 3.63 (Absolute und relative Extremstellen)

Wir setzen Musteraufgabe 3.60 fort und suchen das (absolute) Maximum der Funktion \(f(x)=x^3-3x\) auf dem Intervall \([-3,3]\).

Das Maximum kann ein relatives Maximum oder ein Randmaximum sein. Das einzige relative Maximum liegt an der Stelle \(x=-1\) und beträgt \(f(-1)=2\). An den Rändern des Definitionsintervalls hat die Funktion die Werte \(f(-3)=-18\) und \(f(3)=18\). Folglich besitzt die Funktion an der Stelle \(x=3\) ein absolutes Maximum. Es handelt sich um ein Randmaximum.

3.4.2 Analyse der Wölbungseigenschaften

Es gibt zwei Möglichkeiten für einen Funktionsgraphen, gewölbt zu sein. Er kann konvex oder konkav sein. Konvex bedeutet, dass das Steigungsverhältnis monoton wächst, konkav bedeutet, dass das Steigungsverhältnis monoton fällt.

Wenn eine Funktion differenzierbar ist, dann ist es möglich, die Wölbung des Funktionsgraphen an ihrer Ableitung abzulesen. Dies ist eine bequeme Methode um festzustellen, ob eine Funktion konvex oder konkav ist.

Eine kleine Vorbemerkung ist vielleicht erforderlich. Wir haben bis jetzt immer nur die Ableitung einer Funktion \(f\) an einem festen Punkt \(x\) untersucht, dh. wir haben die Zahl \(f'(x)\) angesehen. Wir können aber auch \(x\) als Variable auffassen und kommen so zur Ableitungsfunktion \(f':x\mapsto f'(x)\). Für die Ableitungsfunktion sind alle Konzepte verwendbar, die wir für Funktionen zu Verfügung haben: Man kann untersuchen, ob die Ableitungsfunktion stetig ist, ob sie differenzierbar ist, ob sie monoton ist, usw. Die Auffassung der Ableitung als Funktion wird sich im folgenden als sehr nützlich herausstellen. Die Sprechweise ist allerdings eher ungenau. Man spricht nämlich meist nicht von der Ableitungsfunktion, wenn man die Ableitungsfunktion \(f'\) meint, sondern nennt diese Funktion auch einfach die Ableitung von \(f\). Aus dem Zusammenhang ist meist klar, was gemeint ist.

Satz 3.64 Es sei \(y=f(x)\) eine differenzierbare Funktion auf einem Intervall \((a,b)\).

1. Ist \(f'\) auf dem Intervall streng monoton wachsend, dann ist \(f\) auf dem Intervall konvex.

2. Ist \(f'\) auf dem Intervall streng monoton fallend, dann ist \(f\) auf dem Intervall konkav.

Begründung: Die Aussage des Satzes ist wieder anschaulich plausibel. Da die Ableitung annähernd das Steigungsverhältnis des Funktionsgraphen auf kleinen Intervallen angibt, hängt die Monotonie der Ableitung offensichtlich mit der Monotonie des Steigungsverhältnisses zusammen.

Ein exakter Beweis beruht auf dem Mittelwertsatz. Sind \(x<y<z\) drei Punkte des Definitionsintervalls der Funktion \(f\), dann gibt es nach dem Mittelwertsatz Zwischenpunkte \(u\in(x,y)\) und \(v\in(y,z)\), sodass \[ \begin{gathered} f'(u)=\frac{f(y)-f(x)}{y-x},\quad f'(v)=\frac{f(z)-f(y)}{z-y}. \end{gathered} \] Wenn nun \(f'\) streng monoton wachsend ist, dann ist \(f'(u)<f'(v)\) und daher gilt \[ \begin{gathered} \frac{f(y)-f(x)}{y-x}<\frac{f(z)-f(y)}{z-y}. \end{gathered} \]

Indem wir den Graphen der Ableitung \(f'(x)\) zeichnen, können wir feststellen, auf welchen Intervallen die Ableitungsfunktion \(f'(x)\) monoton wächst oder monoton fällt, und daraus können wir ablesen, auf welchen Intervallen die Funktion \(f(x)\) konvex oder konkav ist.

Aber wir können noch einen Schritt weiter gehen. Wenn die Ableitung \(f'\) selbst wieder eine differenzierbare Funktion ist, sind, wie wir wissen, die Monotonieeigenschaften von \(f'\) an der Ableitung \((f')'\) abzulesen. Wenn man die Ableitung \((f')'\) der Ableitungsfunktion \(f'\) bildet, so entsteht die sogenannte zweite Ableitung \((f')'=:f''\).

Wir fassen nun die Schlussfolgerungen zusammen, die wir aus dem Studium der zweiten Ableitung ziehen können:

• Wenn die zweite Ableitung \(f''\) auf einem Intervall positiv ist, dann ist die erste Ableitung \(f'\) dort streng monoton wachsend. Daraus folgt, dass die Funktion \(f\) dort konvex ist.

• Ist die zweite Ableitung \(f''\) auf einem Intervall negativ, dann ist die erste Ableitung \(f'\) dort streng monoton fallend und die Funktion \(f\) ist konkav.

• Ist die zweite Ableitung an einem Punkt gleich Null und ändert sich dort das Vorzeichen der zweiten Ableitung, so ändert sich dort zugleich die Richtung der Wölbung der Funktion \(f\). Man spricht dann von einem Wendepunkt der Funktion \(f\).

Man kann die Wölbung dazu benutzen, um kritische Punkte zu interpretieren:

Satz 3.65 (Klassifikation von kritischen Punkten) Es sei \(f\) eine zweimal differenzierbare Funktion und \(x_0\) ein kritischer Punkt. Dann gilt: \[ \begin{gathered} f'(x_0) = 0,\quad f''(x_0) < 0 \implies x_0 \text{ ist ein relatives Maximum}\\ f'(x_0) = 0,\quad f''(x_0) > 0 \implies x_0 \text{ ist ein relatives Minimum} \end{gathered} \]

Begründung: Ist \(f''(x_0)<0\), dann gibt es ein Intervall um \(x_0\), wo \(f'\) streng monoton fallend ist. Folglich ist \(f'(x)>0\) für \(x<x_0\) nahe bei \(x_0\) und \(f'(x)<0\) für \(x>x_0\) nahe bei \(x_0\). Daher ist \(x_0\) ein relatives Maximum.

Den zweiten Teil beweist man ähnlich. □

Musteraufgabe 3.66 Man bestimme und klassifiziere die kritischen Punkte der Funktion \(f(x)=3xe^{-x^2/8}\), siehe Abbildung 3.13.

Abbildung 3.13: Die Funktion \(f(x)=3xe^{-x^2/8}\).

Lösung: Wir bilden die 1. Ableitung: \[ \begin{gathered} f'(x)=3e^{-x^2/8}+3x\left(-\frac{2x}{8}\right)e^{-x^2/8}=\frac{3}{4}e^{-x^2/8} (4-x^2). \end{gathered} \] Die 1. Ableitung hat die Form eines Produkts, wobei der erste Faktor als Exponentialfunktion niemals Null werden kann. Daher folgt aus Nullsetzen des zweiten Faktors; \[ \begin{gathered} 4-x^2=0\implies x_1=-2, \quad x_2=2. \end{gathered} \] Die Funktion hat daher kritische Punkte an den Stellen \(x=\pm 2\).

Wir benötigen noch die zweite Ableitung \(f''(x)\). Mit etwas Rechnerei finden wir: \[ \begin{gathered} f''(x)=-\frac{3x}{16}(12-x^2)e^{-x^2/8}. \end{gathered} \] Daraus folgt: \[ \begin{gathered} f''(-2)=3\cdot e^{-1/2}>0\implies \text{rel. Minimum in }x=-2, \end{gathered} \] und \[ \begin{gathered} f''(2)=-3\cdot e^{-1/2}<0\implies \text{rel. Maximum in }x=2. \end{gathered} \] □

3.5 Anwendungen – Optimierung

Die Bestimmung von relativen Maxima und Minima ist ein einfaches Beispiel für die Lösung nichtlinearer Optimierungsprobleme. Wir wollen nun einige ökonomische Anwendungsbeispiele solcher Optimierungsprobleme diskutieren.

3.5.1 Gewinnoptimierung bei vollständiger Konkurrenz

Es sei \(p\) der feste Preis, mit dem ein Mengenanpasser in einem Konkurrenzmarkt zu rechnen hat. Bezeichnet \(C(x)\) die Kostenfunktion des Mengenanpassers, dann beträgt sein Gewinn \[ \begin{gathered} \pi(x)=px-C(x). \end{gathered} \] Handelt es sich um eine lineare Kostenfunktion \(C(x)=kx+d\), und ist \(p>k\) (der Verkaufspreis höher als die Stückkosten), dann gibt es genau eine Gewinnschwelle \(x=x_0\), ab der der Gewinn positiv ist. Der Gewinn steigt dann mit der produzierten Menge \(x\) und ist nach oben nur durch die Kapazität des Produzenten beschränkt. Eine Gewinnoptimierung macht dann keinen Sinn.

Wenn aber die Kostenfunktion nichtlinear ist, dann können ganz andere Verhältnisse vorliegen. Es kann zum Beispiel so sein, dass die Kostenfunktion die Form \[ \begin{gathered} C(x)= V(x)+d \end{gathered} \] hat, wobei die variablen Kosten \(V(x)\) nun nichtlinear sind. Wenn eine solche Situation vorliegt, dann kann es durchaus sein, dass der erzielbare Gewinn durch Wahl einer geeigneten Produktionsmenge optimiert werden muss.

Musteraufgabe 3.67 Ein Produktionsunternehmen ist in der Lage, jede Menge seines Produkts zum Preis von 10000 GE pro Stück (Marktpreis) zu verkaufen. Die Kostenfunktion sei: \[ \begin{gathered} C(x)=\frac{x^3}{10}-60x^2+10000x+1200000. \end{gathered} \] Welche Produktionsmenge maximiert den Gewinn?

Lösung: Die Gewinnfunktion (Abbildung 3.14) lautet \[ \begin{aligned} \pi(x)&=R(x)-C(x)\\ &=10000x-\left(\frac{x^3}{10}-60x^2+10000x+1200000\right)\\ &=-\frac{x^3}{10}+60x^2-1200000.\end{aligned} \]

Abbildung 3.14: Zu Musteraufgabe 3.67.

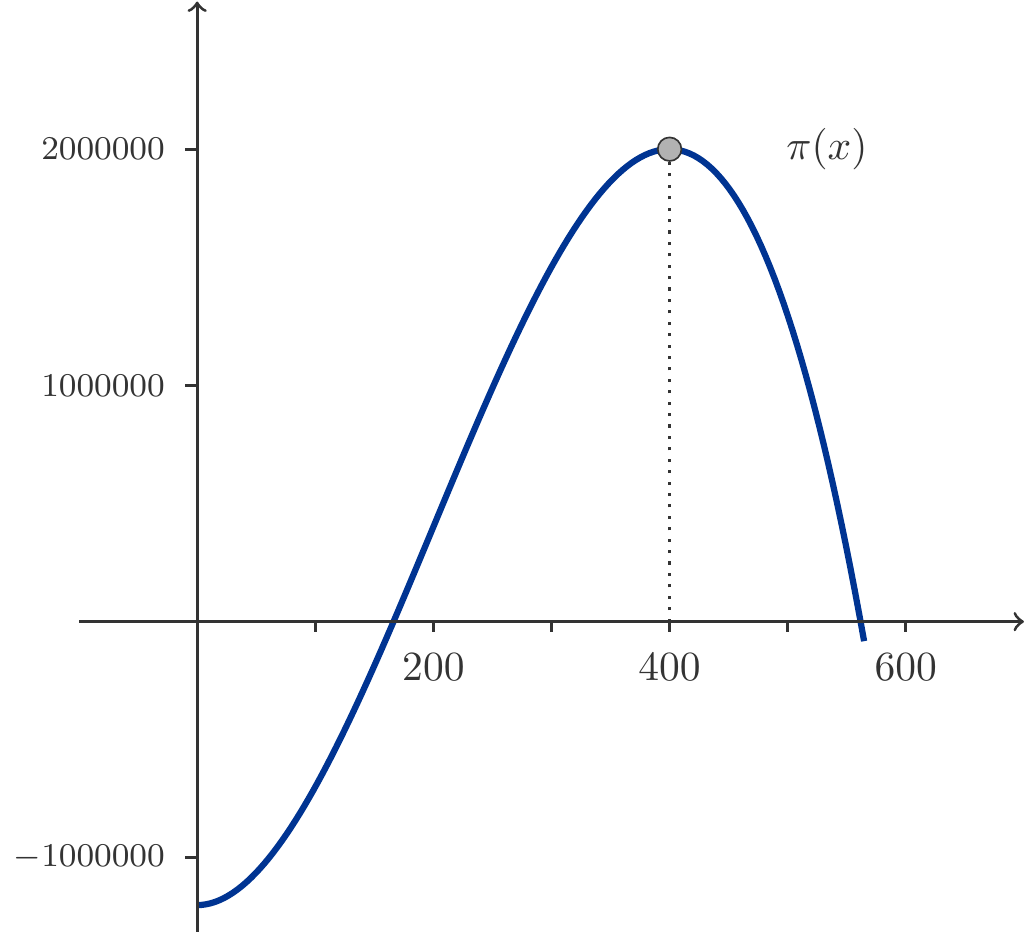
Ihre erste Ableitung ist: \[ \begin{gathered} \pi'(x)=-\frac{3x^2}{10}+120x = -\frac{3x}{10}(x-400). \end{gathered} \] Aus \(\pi'(x)=0\) ergeben sich die beiden kritischen Punkte \(x_1=0\) und \(x_2=400\).

Die zweite Ableitung \[ \begin{gathered} \pi''(x)=-\frac{3x}{5}+120 \end{gathered} \] hat in den kritischen Punkten die Werte \(\pi''(0)=120\) und \(\pi''(400)=-120\). Folglich ist \(x_2=400\) ein relatives Maximum.

Als Randmaximum des Definitionsbereichs \([0,\infty)\) kommt nur \(x_2=400\) in Frage. Da \(\pi(400)=2000000\) und \(\pi(0)=-1200000\), ist das relative Maximum bei \(x_2=400\) zugleich das absolute Maximum. Dh.: Mit der Produktion von 400 Stück wird der Gewinn maximiert. □

3.5.2 Das Betriebsminimum

Eine weitere Fragestellung im Rahmen der Mengenanpassung bei vollständiger Konkurrenz bezieht sich auf den Mindestpreis \(p\), bei dem noch angeboten wird. Wenn die Kostenfunktion linear ist, ist auch die Antwort auf diese Frage sehr einfach: Der Preis \(p\) muss höher als die Stückkosten sein. Wenn aber die Kostenfunktion nichtlinear ist, dann ist die Sache etwas komplizierter und führt im Grunde wieder auf ein Optimierungsproblem.

Kurzfristig kann ein Mengenanpasser auf die Deckung seiner Fixkosten verzichten. Unter allen Umständen sollte aber der Erlös die variablen Kosten abdecken. Es muss daher gelten: \[ \begin{gathered} \text{Erlös} - \text{variable Kosten} \ge 0, \\ px-V(x)\ge 0 \implies p\ge \frac{V(x)}{x} =\overline{V}(x)= \text{durchschnittliche variable Kosten}. \end{gathered} \]

Der Preis muss also stets mindestens so hoch sein wie die durchschnittlichen variablen Kosten.

Unter dem Betriebsminimum versteht man jene Menge, bei der diese durchschnittlichen variablen Kosten minimal sind. Die Höhe dieser minimalen durchschnittlichen variablen Kosten ist dann zugleich der Mindestpreis, zu dem überhaupt noch ein Angebot zustande kommt: \[ \begin{gathered} p_{\min}=\overline{V}(x_{\min}). \end{gathered} \]

Musteraufgabe 3.68 Wie hoch sind Betriebsminimum und Mindestpreis eines Mengenanpassers mit der Kostenfunktion \[ \begin{gathered} C(x)=\frac{x^3}{10}-60x^2+10000x+1200000\;? \end{gathered} \]

Lösung: Die durchschnittlichen variablen Kosten betragen \[ \begin{gathered} \overline{V}(x)=\frac{1}{x}\left(\frac{x^3}{10}-60x^2+10000x\right) =\frac{x^2}{10}-60x+10000. \end{gathered} \] Das ist eine quadratische Funktion, deren Minimum im Scheitel angenommen wird: \[ \begin{gathered} x_{\min}=\frac{60}{2/10}=300, \\[5pt] p_{\min}=\overline{V}(300) =1000\,\text{GE}, \end{gathered} \] wobei \(p_{\min}=1000\) der Mindestpreis ist, der erzielbar sein muss, damit das Unternehmen überhaupt bereit ist, als Anbieter aufzutreten. □

3.5.3 Preispolitik eines Monopolisten

Mit der Preispolitik eines Monopolisten haben wir uns schon mehrmals beschäftigt. Nun sind wir in der Lage, die damit zusammenhängenden Fragen sehr allgemein zu behandeln.

Ein Monopolist ist in der Lage, den Preis \(p\) zu variieren. Er ist konfrontiert mit einer Reaktion des Marktes, die durch die Nachfragefunktion \(D(p)\) zusammengefasst wird. Der Erlös des Monopolisten beträgt \[ \begin{gathered} R(p)=pD(p), \end{gathered} \] und sein Gewinn beträgt \[ \begin{gathered} \pi(p)=R(p)-C(D(p))=pD(p)-C(D(p)), \end{gathered} \] wobei \(C(x)\) die (möglicherweise nichtlineare) Kostenfunktion bezeichnet.

Bei der Gewinnoptimierung eines Monopolisten ist es manchmal unzweckmäßig, die Gewinnfunktion \(\pi\) als Funktion des Preises anzugeben. Der Grund für diese Unzweckmäßigkeit besteht darin, dass es aufwendig sein kann, eine nichtlineare Kostenfunktion \(C(x)\) mit der Nachfragefunktion \(D(p)\) zu verketten. Es ist dann meist viel einfacher, den Gewinn als Funktion der abgesetzten Menge darzustellen.

Musteraufgabe 3.69 Ein Unternehmen besitzt aufgrund eines Patents ein Monopol auf einen Wirkstoff, der von der Pharmaindustrie nachgefragt wird. Die Nachfragefunktion nach diesem Produkt lautet bei einem Preis \(p\): \[ \begin{gathered} D(p): x=200 e^{-0.01p}\qquad 0<x<200;\text{ $x$ in Tonnen}. \end{gathered} \] Die Produktionskosten sind eine lineare Funktion der Ausbringungsmenge \(x\): \[ \begin{gathered} C(x)=1500+50x. \end{gathered} \]

1. Welchen Gewinn erzielt das Unternehmen, wenn es seinen Erlös maximiert?

2. Welchen Gewinn kann das Unternehmen maximal erzielen?

Lösung: Um den Erlös zu maximieren, könnten wir die Erlösfunktion so wie bisher als Funktion des Preises darstellen. Da wir aber den dabei erzielten Gewinn auch noch ausrechnen wollen, gehen wir gleich von Beginn an zu der Darstellung als Funktion der abgesetzten Menge über.

Wir berechnen die inverse Nachfragefunktion, also die Funktion, die uns zu jeder Menge \(x\) den Preis \(p\) angibt, der zum vollständigen Verkauf dieser Menge \(x\) führt: \[ \begin{gathered} D(p): x=200 e^{-0.01p}\quad\implies \quad D^{-1}(x): p=-100\ln x+100\ln(200). \end{gathered} \] Damit nimmt die Erlösfunktion die folgende Form an: \[ \begin{gathered} R(x) = p \cdot x = -100 x \ln x + 100 x \ln(200).\qquad \mbox{(A)} \end{gathered} \] Die Gewinnfunktion lautet: \[ \begin{aligned} \pi(x)&=R(x)-C(x)\\[5pt] &=-100x\ln x+100x\ln(200)-50x-1500.\qquad \mbox{(B)} \end{aligned} \] (a) Um das Erlösmaximum zu finden, bilden wir die Grenzerlöse \(R'(x)\) (Produktregel!): \[ \begin{aligned} R'(x)&= -100\ln x-100+100\ln(200)\\[5pt] &=-100\left(\ln x+1-\ln(200)\right). \end{aligned} \] Nullsetzen der Grenzerlöse, d.h. \(R'(x)=0\), führt auf die Gleichung: \[ \begin{gathered} \ln x+1-\ln(200)=0\implies \ln x=\ln(200)-1. \end{gathered} \] Diese Gleichung besitzt die eindeutige Lösung: \[ \begin{gathered} x=e^{\ln(200)-1}=\frac{200}{e}\simeq 73.58. \end{gathered} \] Dies ist tatsächlich das Maximum der Erlösfunktion, denn \[ \begin{gathered} R''(x)=-\frac{100}{x}<0\quad\text{für alle }x>0. \end{gathered} \] Welchen Gewinn erzielt das Unternehmen mit dieser Strategie?

Wir setzen \(x=200/e\) in die Gewinnfunktion ein und bedenken dabei: \[ \begin{gathered} \ln\left(\frac{200}{e}\right)=\ln(200)-1. \end{gathered} \] So erhalten wir: \[ \begin{aligned} \pi\left(\frac{200}{e}\right)&=-\frac{20000}{e}\left(\ln(200)-1\right) +\frac{20000}{e}\ln(200)-\frac{10000}{e}-1500\\[5pt] &=\frac{10000}{e}-1500\simeq 2178.8 \text{ GE}. \end{aligned} \]

(b) Nun die zweite Strategie, die zweifellos von kaufmännischer Vorsicht bestimmt ist: wir bilden die erste Ableitung der Gewinnfunktion (gegeben in (B)) und setzen diese Null: \[ \begin{aligned} \pi'(x)&=-100\ln x-150+100\ln(200) = 0,\\[5pt] \ln x&=\ln(200)-\frac{3}{2}\implies x=\frac{200}{e^{3/2}}\simeq 44.626. \end{aligned} \] Die Leserinnen verifizieren leicht, dass \(\pi''(x)=-100/x\). Die Gewinnfunktion besitzt daher ein eindeutiges Maximum in \(x=200/e^{3/2}\). Der bei diesem Absatz erzielte Gewinn beträgt: \[ \begin{aligned} \pi\left(\frac{200}{e^{3/2}}\right)&=\frac{20000}{e^{3/2}}-1500\simeq 2962.6 \end{aligned} \] □

3.5.4 Optimale Lagerhaltung

Als weitere Anwendung untersuchen wir ein berühmtes Problem der Lagerhaltungstheorie, das Economic Order Quantity Modell (EOQ).

Wir stellen uns ein Handelsunternehmen vor, das ein Produkt vertreibt, welches es selbst bei einem Hersteller beschaffen muss. Dieses Produkt wird in ausreichenden Mengen auf Lager gelegt, um die Nachfrage der Kunden decken zu können.

Weiters nehmen wir an, dass die Nachfrage konstant ist in dem Sinn, dass das Produkt mit konstanter Rate \(\lambda\) dem Lager entnommen wird. Die Rate \(\lambda\) messen wir in Stück oder ME pro Zeiteinheit.

In gewissen Zeitabständen erfolgen neue Bestellungen beim Hersteller des Produkts, die bestellten Mengen werden geliefert und dem zur Zeit \(t\) aktuellen Lagerbestand \(I(t)\) hinzu gefügt.

Wie entwickelt sich der Lagerbestand \(I(t)\) im Laufe der Zeit? In Abbildung 3.15 ist ein typischer Lagerbestandsverlauf graphisch dargestellt.

Abbildung 3.15: Typischer Lagerbestandsverlauf \(I(t)\).

Das ist ein sehr merkwürdiges, sägezahnartiges Muster, das sich so erklären lässt:

• Die Funktion \(I(t)\) weist Sprungstellen auf an den Lieferzeitpunkten. Die Höhe der Sprünge entspricht den gelieferten Mengen. Im EOQ-Modell wird in der einfachsten Variante unterstellt, dass das, was bestellt wurde, auch geliefert wird.

• Zwischen den Sprungstellen nimmt \(I(t)\) linear mit Anstieg \(-\lambda\) ab, denn wir nehmen an, dass das Produkt mit konstanter Rate dem Lager entnommen wird.

Wenn wir dem Modell eine einfache, dennoch plausible Kostenstruktur, die wir gleich besprechen werden, unterstellen, so erweist es sich, dass der Bestandsverlauf in Abbildung 3.15 nicht optimal ist.

Anschaulich gesprochen wird Optimalität im Sinne von kleinstmöglichen Kosten erreicht, wenn wir das etwas erratische Bild der Lagerbestandsfunktion \(I(t)\) soweit als möglich beruhigen. Das wird erreicht durch:

• Bestelle immer die gleiche Menge \(x\).

• Setze die Bestellungen zeitlich so an, dass eine neue Lieferung gerade dann eintrifft, wenn der Lagerbestand auf Null sinken würde.

So ergibt sich ein idealer Bestandsverlauf, wie er in Abbildung 3.16 zu sehen ist.

Abbildung 3.16: Idealer Lagerbestandsverlauf \(I(t)\).

Dem EOQ-Modell liegt folgende einfache Kostenstruktur zugrunde:

• Jeder Bestellvorgang verursacht fixe, von der Höhe der Bestellmenge \(x\) unabhängige Kosten im Ausmaß \(K\).

• Das bestellte Produkt muss beim Hersteller bezahlt werden, der Einstandspreis beträgt \(c\) GE pro Stück.

• Die gelieferten Mengen müssen auf Lager gelegt werden, dafür fallen Kosten für die eigentliche physische Lagerung (holding cost) in der Höhe \(h\) (GE pro Stück und Zeiteinheit) an.

Wir legen uns nun auf eine Zeiteinheit fest, z.B. ein Jahr³.

Die Gesamtkosten \(C(x)\) bei einer Bestellmenge \(x\) ergeben sich auf diese Weise:

• Bei einem Bedarf von \(\lambda\) Stück pro Jahr sind \(\lambda/x\) Bestellvorgänge erforderlich. Dies ergibt einen Kostenbeitrag von \(K\lambda/x\).

• Der Bedarf \(\lambda\) ist beim Lieferanten zu bezahlen, die Kosten betragen \(c\lambda\).

• Da der Lagerbestand gleichmäßig, also linear von \(x\) auf 0 abgebaut wird, beträgt der durchschnittliche Bestand \(x/2\), die halbe Höhe der Sägezähne. Die Kosten für die physische Lagerung sind daher im Mittel \(hx/2\).

Daraus ergeben sich Gesamtkosten pro Zeiteinheit bei einer Bestellmenge \(x\): \[ \begin{gathered} C(x)=\frac{K\lambda}{x}+c\lambda+h\,\frac{x}{2}. \end{gathered} \tag{3.47}\] Wir suchen die optimale Bestellmenge \(x^\ast\), die ein Minimum von (3.47) sicherstellt. Wir gehen wie üblich vor: \[ \begin{aligned} C'(x)=-\frac{K\lambda}{x^2}+\frac{h}{2}=0. \end{aligned} \] Diese einfache quadratische Gleichung besitzt eine positive Lösung: \[ \begin{gathered} x^\ast=\sqrt{\frac{2K\lambda}{h}}\,. \end{gathered} \tag{3.48}\] Dies ist die berühmte Wilson-Harris Formel für die optimale Bestellmenge im EOQ-Modell. Mit Hilfe von \(x^\ast\) können wir auch leicht berechnen, in welchen Zeitabständen die Bestellungen idealerweise erfolgen sollen. Dazu müssen wir nur die optimale Bestellmenge durch den Bedarf \(\lambda\) dividieren: \[ \begin{gathered} t^\ast=\frac{x^\ast}{\lambda}=\sqrt{\frac{2K}{h\lambda}}. \end{gathered} \tag{3.49}\] Dass \(x^\ast\) tatsächlich ein Minimum ist, erkennen wir an der 2. Ableitung: \[ \begin{gathered} C''(x)=\frac{2K\lambda}{x^3}>0\quad\text{für alle }x>0. \end{gathered} \]

Abbildung 3.17: Lagerkosten mit Minimum.

Musteraufgabe 3.70 Ein Handelsunternehmen vertreibt ein Produkt, von dem pro Jahr \(50\,000\) Stück abgesetzt werden. Die Lagerung verursacht Kosten pro Stück und Jahr von 0.4 GE. Der Einstandspreis beträgt 4 GE pro Stück, die Fixkosten eines Beschaffungsvorganges 400 GE.

1. Was ist die optimale Bestellmenge?

2. Wie oft pro Jahr muss ein Bestellvorgang durchgeführt werden?

3. Was ist der optimale Zeitabstand (in Tagen) zwischen Bestellungen?

Lösung: Als Zeiteinheit wählen wir 1 Jahr. Wir entnehmen der Angabe: \[ \begin{aligned} %% {alignat*}{2} \lambda &=50000 &\quad & \text{Bedarf}\\ K&=400 & & \text{bestellfixe Kosten}\\ c&=4 && \text{Einstandspreis}\\ h &= 0.4 && \text{Lagerkostensatz}\end{aligned} \] Dies ergibt die Kostenfunktion (3.47): \[ \begin{gathered} C(x)=\frac{K\lambda}{x}+c\lambda+h\,\frac{x}{2}=\frac{20000000}{x} +200000 + 0.2x,\\ C'(x)=-\frac{20000000}{x^2}+0.2 =0,\\ x_1=-10000,\quad x_2=10000. \end{gathered} \] Die optimale Bestellmenge ist daher \(x^\ast=10000\) Stück.

Da der Jahresbedarf 50000 Stück beträgt, müssen \(50000/10000=5\) Bestellvorgänge pro Jahr abgewickelt werden.

Der optimale Zeitabstand zwischen zwei Bestellungen ist \[ \begin{gathered} t^\ast =\frac{x^\ast}{\lambda}=\frac{10000}{50000}=0.2\text{ Jahre} = 73 \text{ Tage}. \end{gathered} \] □

Musteraufgabe 3.71 Ein Electronic Shop vertreibt unter anderem Flatscreens (55 Zoll Bildschirmdiagonale), deren Einstandspreis 348 GE beträgt. Durchschnittlich werden pro Woche 1900 dieser Geräte verkauft. Die Lagerkosten eines Geräts betragen 2.40 GE pro Stück und Woche. Ein Bestellvorgang beim Hersteller der Geräte verursacht Personalkosten von 1200 GE und Abwicklungskosten (Transport usw.) von 2430 GE. Das Unternehmen rechnet mit Finanzierungskosten von 9 % pro Jahr (entgangene Zinsen für den Kapitalwert von gelagerten Gütern).

1. Welche Menge an Flatscreens soll bei jedem Bestellvorgang bestellt werden, sodass die Gesamtkosten der Lagerhaltung minimal werden?

2. In welchen Zeitabständen sollen diese Bestellungen vorgenommen werden?

Lösung: Wir rechnen mit der Zeiteinheit 1 Woche. Dabei ist zu beachten, dass der Zinssatz ein Jahreszins, der entsprechend umgerechnet werden muss.

(a) Der Bedarf pro Woche beträgt \(\lambda=1900\) Stück. Wir stellen zunächst die fixen Kosten \(K\) und die variablen Kosten \(c\) pro Bestellvorgang auf: \[ \begin{aligned} K&=\text{Abwicklungskosten}+\text{Personalkosten}\\ &=1200+2430 =3630, \\ c&=\text{Einstandspreis}=348. \end{aligned} \] Zum Lagerkostensatz \(h\): er setzt sich zusammen aus den Kosten für die physische Lagerung der Geräte und den entgangenen Zinsen für das im Lager gebundene Kapital: \[ \begin{aligned} h&=2.4+348\cdot \frac{0.09}{52}=3.0023\,. \end{aligned} \]

Die Gesamtkosten bei einer Bestellmenge \(x\) setzen sich dann wie folgt zusammen: \[ \begin{aligned} C(x)&=\frac{K\cdot \lambda}{x}+c\cdot \lambda+\frac{h}{2}\cdot x \\ &=\frac{3630\cdot 1900}{x}+348\cdot 1900+3.0023\cdot \frac{x}{2}\,. \end{aligned} \] Diese Gesamtkosten sind minimal für die Bestellmenge \[ \begin{gathered} x^\ast=\sqrt{\frac{2K\lambda}{h}} =\sqrt{\frac{2\cdot 3630\cdot 1900}{3.0023}} =2143.5\,. \end{gathered} \]

(b) Das optimale Bestellintervall ergibt sich aus: \[ \begin{gathered} t^\ast=\frac{x^\ast}{\lambda}=\frac{2143.5}{1900} = 1.1281\text{ Wochen}\simeq 8 \text{ Tage}. \end{gathered} \] □

3.5.5 Weitere Optimierungsaufgaben

Musteraufgabe 3.72 (Nutzungsdauer einer Investition) Die Anschaffungskosten einer Maschine betragen 300 000 GE, die Betriebskosten wachsen von 25 000 GE im ersten Jahr jährlich um den Betrag 25 000 GE. Welche Nutzungsdauer verursacht die niedrigsten durchschnittlichen Gesamtkosten?

Lösung: Die Betriebskosten der einzelnen Jahre bilden eine arithmetische Folge mit Summe \(B(n)\) über die ersten \(n\) Glieder. Das sind die aufgelaufenen Gesamtbetriebskosten nach dem \(n\)-ten Betriebsjahr. Wir haben \[ \begin{gathered} B(1)=25000,\quad B(n)=25000+25000(n-1)=25000n. \end{gathered} \] Mit Hilfe der Summenformel (1.8): \[ \begin{gathered} S(n)=\frac{n}{2}\left(B(1)+B(n)\right)=12500n(n+1). \end{gathered} \] Die Gesamtkosten nach der Nutzungszeit \(t\) sind daher (wir setzen \(n=t\)): \[ \begin{gathered} C(t)=300\,000+12\,500t+12\,500t^2. \end{gathered} \] Es ist jene Nutzungszeit \(t\) zu bestimmen, für die die durchschnittlichen Kosten \[ \begin{gathered} \overline{C}(t)=\frac{C(t)}{t}=\frac{300\,000}{t}+12\,500+12\,500t \end{gathered} \] minimal sind.

Wir ermitteln die erste Ableitung und setzen diese Null: \[ \begin{gathered} \overline{C}'(t)=-\frac{300000}{t^2}+12500=0,\\ t =\sqrt{\frac{300000}{12500}}= 4.899\;\text{Jahre}. \end{gathered} \] □

Beispiel 3.73 (Optimaler Verkaufszeitpunkt)

Jemand erwirbt ein Gut zu Anschaffungskosten von \(I_0\) GE, um es zu einem späteren Zeitpunkt wieder zu verkaufen. Der Wiederverkaufswert \(R(t)\) ist eine bekannte Funktion der Zeit \(t\).

• Was ist der optimale Zeitpunkt \(T\), um das Gut zu verkaufen, unter der Annahme, dass der Besitz des Gutes keine nennenswerten Kosten verursacht?

• Unter welchen Bedingungen existiert so ein optimaler Zeitpunkt?

Um \(T\) zu finden, argumentieren wir so: der Gewinn aus dem Verkauf, der zur Zeit \(t\) erzielt wird, ist die Differenz aus \(R(t)\) und dem Endwert \(I_0e^{ct}\), wenn \(I_0\) statt für den Kauf des Gutes verwendet zu werden, angelegt worden wäre zu einem Zinssatz \(c\) (kontinuierliche Verzinsung). Äquivalent dazu ist der Barwert des Gewinns, den wir durch Abzinsen erhalten: \[ \begin{gathered} \pi(t)=R(t)e^{-ct}-I_0. \end{gathered} \] Wir bilden die erste Ableitung und setzen diese Null: \[ \begin{gathered} \pi'(t)=e^{-ct}\left(R'(t)-cR(t)\right)=0. \end{gathered} \] Da \(e^{-ct}>0\), muss ein kritischer Punkt \(t\) die Gleichung \(R'(t)-cR(t)=0\) erfüllen. Daraus folgt: \[ \begin{gathered} \frac{R'(t)}{R(t)}=c. \end{gathered} \tag{3.50}\] Diese Bedingung ist interessant, denn sie besagt, das die relative Änderungsrate des Wiederverkaufswertes gleich sein muss dem Zinssatz der Alternativanlage.

Es sei \(T\) eine Lösung von (3.50), also \(R'(T)-cR(T)=0\). Damit sich an der Stelle \(T\) ein lokales Maximum befindet, muss \(\pi''(T)<0\) sein. \[ \begin{aligned} \pi''(T)&=e^{-cT}\bigg[R''(T)-cR'(T)-c \big(\underbrace{R'(T)-cR(T)}_{=0}\big)\bigg]\\[5pt] &=e^{-cT}\big(R''(T)-cR'(T)\big)<0. \end{aligned} \] Diese letzte Bedingung kann nur erfüllt sein, wenn \[ \begin{gathered} (R''(T)-cR'(T)<0\implies \frac{R''(T)}{R'(T)}<c \end{gathered} \tag{3.51}\] Mit anderen Worten, ein kritischer Punkt ist genau dann ein Maximum, wenn die relative Änderungsrate von \(R'(T)\) kleiner ist als der Zinssatz.

Musteraufgabe 3.74 Eine Investorin beschließt, sich mit 10000 GE an einem Startup-Unternehmen zu beteiligen. Ausführliche statistische Analysen über das Potential der Beteiligung ergaben, dass folgendes Szenario am wahrscheinlichsten ist: der Wert der Anlage wird in den nächsten Jahren linear um 25% pro Jahr steigen.

Was wäre ein idealer Zeitpunkt die Beteiligung zu verkaufen, wenn die Möglichkeit besteht, alternativ das Kapital risikofrei mit garantierten 10% Rendite zu veranlagen?

Lösung: Der Wiederverkaufswert der Beteiligung ist \[ \begin{gathered} R(t)=10000(1+0.25t). \end{gathered} \] Der Barwert des Gewinns aus dem Verkauf der Beteiligung zur Zeit \(t\) beträgt: \[ \begin{gathered} \pi(t)=10000(1+0.25t)e^{-0.1t}-10000. \end{gathered} \] Die Bedingung (3.50) lautet: \[ \begin{gathered} \frac{2500}{10000(1+0.25t)}=0.1\implies t=\frac{1500}{250}=6. \end{gathered} \] Der optimale Zeitpunkt des Verkaufs der Beteiligung ist also nach \(T=6\) Jahren. Dass zu diesem Zeitpunkt wirklich maximaler Gewinn erzielt wird, ergibt sich aus der Bedingung (3.51), die hier automatisch erfüllt ist. Denn \(R''(t)=0<0.1\) für alle \(t\), und damit \(R''(t)/R'(t)=0\). Eine graphische Illustration des allgemeineren Fall eines linearen Wiederverkaufswerts \(R(t)=I_0(a+bt)\) ist in Abbildung 3.18 dargestellt. □

Abbildung 3.18: Optimaler Verkaufszeitpunkt.

3.6 Weitere Übungsaufgaben

1. Bestimmen Sie die 1. Ableitung von \(y=3 x^{6}-19 x -9\) an der Stelle \(x=1\).

   Lösung: \(y'=18x^5-19\), \(y'(1)=-1\).

2. Bestimmen Sie die 1. Ableitung von \(y=(2x+3)^4\) an der Stelle \(x=0\).

   Lösung: \(y'=8(2x+3)^3\), \(y'(0)=216\).

3. Bestimmen Sie die 1. Ableitung von \(y=3x^2e^{-x}\) an der Stelle \(x=1\).

   Lösung: \(y'=3x(2-x)e^{-x}\), \(y'(1)=1.1036\).

4. Bestimmen Sie die 1. Ableitung von \(y=(2x-1)^2e^{-x^2/5}\) an der Stelle \(x=0\).

   Lösung: \(\displaystyle y'=-\frac{2}{5}(10-19x-4x^2+4x^3)e^{-x^2/5}\), \(y'(0)=-4\).

5. Bestimmen Sie die 1. Ableitung von \(y=\sqrt{10+3^x}\) an der Stelle \(x=0\).

   Lösung: \(\displaystyle y'=\frac{3^x\ln 3}{2\sqrt{10+3^x}}\), \(y'(0)=0.1656\).

6. Bestimmen Sie die 1. Ableitung von \(y=\ln(1+\sqrt{x})\) an der Stelle \(x=1\).

   Lösung: \(\displaystyle y'=\frac{1}{2\sqrt{x}(1+\sqrt{x})}\), \(y'(1)=1/4\).

7. Bestimmen Sie die 1. Ableitung von \(y=\sqrt{e^{-5x^4}}\) an der Stelle \(x=1\).

   Lösung: \(\displaystyle y'=-10x^3e^{-5x^4/2},\quad y'(1)=-0.8208\).

8. Bestimmen Sie die 1. Ableitung von \(y=\ln(x^{3-\sqrt{x}})\) an der Stelle \(x=1\).

   Lösung: \(\displaystyle y'=-\frac{\ln x}{2\sqrt{x}}+\frac{3-\sqrt{x}}{x}, \quad y'(1)=2\).

9. Bestimmen Sie die 1. Ableitung von \(y=x^{2x}\) an der Stelle \(x=2\).

   Lösung: \(y'=2 x^{2x}(\ln x+1),\quad y'(2)=32(1+\ln 2)=54.1807\).

10. Bestimmen Sie die 1. Ableitung von \(\displaystyle y=\frac{e^{3x}}{1+x}\) an der Stelle \(x=0\).

    Lösung: \(\displaystyle y'=\frac{e^{3x}(2+3x)}{(1+x)^2},\quad y'(0)=2\).

11. Das Bruttoinlandsprodukt eines Landes stieg zwischen 1990 und 2000 von 696 Mrd. GE auf 991 Mrd. GE. Es wird vorausgesetzt, dass die relative Wachstumsrate des BIP konstant ist. Wie hoch ist die relative Wachstumsrate?

    Lösung: 3.53 %

12. Berechnen Sie die relative Änderungsrate \(c(x)\) der Funktion \(f(x)=\sqrt{x}\) an der Stelle \(x=1/2\).

    Lösung: \(\displaystyle c(x)=\frac{1}{2x},\quad c(1/2)=1\).

13. Berechnen Sie die relative Änderungsrate \(c(x)\) der Funktion \(f(x)=2^{x^2-1}\) an der Stelle \(x=1\).

    Lösung: \(\displaystyle c(x)=2x\ln 2,\quad c(1)=2\ln 2\simeq 1.3862\).

14. Berechnen Sie die Elastizität von \(f(x)=e^{-8\sqrt{x}}\) an der Stelle \(x_0=7\).

    Lösung: \(\epsilon(x)=-4\sqrt{x},\;\epsilon(7)=-4\sqrt{7}\simeq -10.58\).

15. Berechnen Sie die Elastizität von \(f(x)=e^{-x^2+5x+3}\) an der Stelle \(x_0=3\).

    Lösung: \(\epsilon(x)=-x(2x-5),\quad \epsilon(3)=-3\).

16. Berechnen Sie die Elastizität von \(f(x)=(2x-5)^3\) an der Stelle \(x_0=1\).

    Lösung: \(\displaystyle \epsilon(x)=\frac{6x}{2x-5},\quad \epsilon(2)=-2\).

17. Gegeben ist die Nachfragefunktion \(q=250p^{-0.2}\). Berechnen Sie die Preiselastizität der Nachfrage.

    Lösung: \(\epsilon(p)=-0.2\).

18. Gegeben ist die Nachfragefunktion \(q=-3p+2400\). In welchem Intervall für \(p\) ist die Nachfrage elastisch?

    Lösung: \(400\le p<800\)

19. Gegeben ist die Nachfragefunktion \(q=-\sqrt{p}+3\). In welchem Intervall für \(p\) ist die Nachfrage elastisch?

    Lösung: \(4\le p<9\).

20. Bestimmen und klassifizieren Sie die lokalen Extremwerte der Funktion \(y=x^2e^{-x/2}\).

    Lösung: Maximum in \(x=4\), Minimum in \(x=0\).

21. Bestimmen und klassifizieren Sie die lokalen Extremwerte der Funktion \(y=x\ln x\).

    Lösung: Minimum in \(x=1/e\simeq 0.3679\).

22. Bestimmen und klassifizieren Sie die lokalen Extremwerte der Funktion \(\displaystyle y=\frac{x-1}{x^2+3x+5}\).

    Lösung: Minimum in \(x=-2\), Maximum in \(x=4\).

23. Bestimmen und klassifizieren Sie die lokalen Extremwerte der Funktion \(y=(2x-1)e^{-x^2}\).

    Lösung: Minimum in \(x=-1/2\), Maximum in \(x=1\).

24. Ein Unternehmen produziert mit Kostenfunktion \[ \begin{gathered} C(x)=9x-4x\ln(x+1)+3x^2. \end{gathered} \] Berechnen Sie die Grenzkosten bei einer Ausbringung von \(x=10\) Einheiten.

    Lösung: \(\displaystyle C'(x)=9-4\ln(x+1)-\frac{4x}{x+1}+6x,\quad C'(10)\simeq 55.77\).

25. Gegeben ist die Nachfragefunktion \(q=25e^{-0.1p}\) eines Monopolisten. Bei welchem Preis wird maximaler Erlös erzielt?

    Lösung: \(p=10\).

26. Ein Unternehmen stellt ein Produkt her, das es zu einem Preis von 221 GE absetzen kann. Die Konkurrenzsituation erlaubt es nicht, den Preis über die Menge langfristig zu beeinflussen. Die Gesamtkosten der Produktion einer Menge \(q\) sind durch die Kostenfunktion gegeben: \[C(q)= 0.0014 q^3- 0.31q^2+ 24.2515 q+27800.\] Welche Menge des Produkts muss abgesetzt werden, damit das Unternehmen maximalen Gewinn erzielt? Runden Sie das Ergebnis auf eine ganze Zahl.

    Lösung: \(q\simeq 302\).

27. Wie hoch ist das Betriebsminimum eines Mengenanpassers mit Kostenfunktion \[ \begin{gathered} C(x)=0.021x^3-34.272x^2+13998x+1100\; ? \end{gathered} \] Was ist der Mindestpreis, der am Markt erzielbar sein muss, damit das Unternehmen überhaupt als Anbieter auftreten wird?

    Lösung: \(x_0=816,\quad p_{\min}=15.024\)

28. Ein Chemieunternehmen besitzt aufgrund eines Patents ein Monopol auf ein spezielles Pflanzenschutzmittel. Die inverse Nachfragefunktion nach diesem Produkt im Großhandel lautet: \[ \begin{gathered} D^{-1}(x): p=- 1.26x+ 349.32\,. \end{gathered} \] An fixen Kosten fallen bei der Produktion 4411 GE an, die variablen Kosten sind durch die Funktion gegeben: \[ \begin{gathered} C_v(x)= 0.006x^3- 0.07x^2+ 32.05x\,. \end{gathered} \] Welchen Gewinn erzielt das Unternehmen, wenn es seinen Umsatz maximiert? Runden Sie das Ergebnis auf eine ganze Zahl.

    Lösung: 721

29. Ein Monopolanbieter besitzt die inverse Nachfragefunktion \(D^{-1}(q)\) und Kostenfunktion \(C(q)\) gegeben durch \[ \begin{aligned} D^{-1}(q): p & = -0.87q + 260.50,\\ C(q) & = 0.020q^3 - 0.12 q^2 + 36.18 q + 2736 \end{aligned} \] Welchen Gewinn kann das Unternehmen maximal erzielen? Runden Sie das Ergebnis auf eine ganze Zahl.

    Lösung: 4105

30. In einem Monopolmarkt hängt die nachgefragte Menge \(x\) vom Preis \(p\) ab als \(x=4500 p^{-1.2}, p>0\). Der Monopolist produziert mit Kostenfunktion \(C(x)=5x+1000\). Bei welcher Absatzmenge \(x_0\), bei welchem Preis \(p_0\) erzielt der Monopolist maximalen Gewinn? Wie hoch ist dieser Gewinn?

    Lösung: \(x_0=75.97,\quad p_0=30\), Gewinn \(\pi=899.36\).

31. Ein Hersteller muss \(144\,000\) Einheiten pro Jahr produzieren. Die Materialkosten betragen \(5\) GE pro Einheit, und die Fixkosten vor jedem Produktionsdurchgang belaufen sich auf \(160\) GE. Die Lagerungskosten betragen \(0.5\) GE pro Stück und Jahr.

    Berechne die optimale Losgröße.

    Lösung: 9600

32. Ein Haushaltsgerätehersteller fertigt unter anderem auch Kühlschränke der Marke Permafrost. In diese Geräte werden Kompressoren eingebaut, deren Einstandspreis 111 GE beträgt. Durchschnittlich werden pro Woche 1200 solcher Kompressoren gebraucht. Die Lagerkosten eines Kompressors betragen 5.55 GE pro Woche. Ein Bestellvorgang beim Hersteller der Kompressoren verursacht Personalkosten von 1530 GE und Abwicklungskosten (Transport usw.) von 1710 GE. Das Unternehmen rechnet mit Finanzierungskosten von 12 % pro Jahr. Berechnen Sie die optimale Bestellmenge. Welches Bestellintervall (in Tagen) garantiert minimale Lagerhaltungskosten? Runden Sie das Ergebnis ganzzahlig.

    Lösung: \(x^\ast =1157.2678\simeq 1157, t^\ast=7\cdot 1157.2678/1200\simeq 7\) Tage.

33. Ein PKW-Hersteller benötigt pro Jahr 40000 Reifen eines bestimmten Typs, die zu einem Stückpreis von 60 GE bezogen werden. Die fixen Kosten betragen 200 GE pro Bestellung. Die Kosten für die Lagerung belaufen sich auf 10 GE pro Reifen und Jahr. Die Geschäftsführung betreibt zur Zeit eine Just-in-Time Lagerhaltungspolitik, das heißt, die erforderlichen Reifen werden täglich angeliefert. Es wird an 365 Tagen im Jahr produziert.

    1. Um welchen Betrag könnten die Kosten der Lagerhaltung gesenkt werden, wenn das Unternehmen eine optimale Lagerhaltung betreibt?

    2. Was wäre tatsächlich das optimale Bestellintervall (in Tagen)?

    Lösung: Kostenvorteil: 60 899.8 GE, Intervall: 12 Tage.

34. Sie haben heute (\(t=0\)) 20 Flaschen Mouton Rothschild Tchelitchev Jahrgang 1956 erworben zu einem Gesamtpreis von 8000 GE. Als Weinkenner wissen Sie, dass der Wiederverkaufswert \(R(t)\) dieses Weines sich nach dem folgenden Gesetz entwickelt: \[ \begin{gathered} R(t)=8000(1+0.5t)^{1.2}\qquad t\text{ in Jahren} \end{gathered} \] Nach wievielen Jahren sollten Sie diesen edlen Wein verkaufen, so dass Ihr Gewinn maximal ist? Rechnen Sie mit einem nominellen Jahreszins von 5% und kontinuierlicher Verzinsung.

    Lösung: 22 Jahre

---

1. Die Gleichung einer Geraden durch einen gegebenen Punkt \((x_0,y_0)\) mit einer gegebenen Steigung \(k\) ergibt sich durch \(\frac{y-y_0}{x-x_0}=k \; \Rightarrow \; y=k(x-x_0)+y_0.\)

2. Ein heuristisches Argument ist nicht logisch zwingend, aber es wirkt als Wegweiser für unsere Fantasie.

3. Es ist belanglos, welche Zeiteinheit wir wählen, nur muss sie in allen Berechnungen konsistent verwendet werden!